Preface
Writing the Bitcoin Book
I first stumbled upon bitcoin in mid-2011. My immediate reaction was more or less "Pfft! Nerd money!" and I ignored it for another six months, failing to grasp its importance. This is a reaction that I have seen repeated among many of the smartest people I know, which gives me some consolation. The second time I came across bitcoin, in a mailing list discussion, I decided to read the whitepaper written by Satoshi Nakamoto to study the authoritative source and see what it was all about. I still remember the moment I finished reading those nine pages, when I realized that bitcoin was not simply a digital currency, but a network of trust that could also provide the basis for so much more than just currencies. The realization that "this isn’t money, it’s a decentralized trust network," started me on a four-month journey to devour every scrap of information about bitcoin I could find. I became obsessed and enthralled, spending 12 or more hours each day glued to a screen, reading, writing, coding, and learning as much as I could. I emerged from this state of fugue, more than 20 pounds lighter from lack of consistent meals, determined to dedicate myself to working on bitcoin.
Two years later, after creating a number of small startups to explore various bitcoin-related services and products, I decided that it was time to write my first book. Bitcoin was the topic that had driven me into a frenzy of creativity and consumed my thoughts; it was the most exciting technology I had encountered since the internet. It was now time to share my passion about this amazing technology with a broader audience.
Intended Audience
This book is mostly intended for coders. If you can use a programming language, this book will teach you how cryptographic currencies work, how to use them, and how to develop software that works with them. The first few chapters are also suitable as an in-depth introduction to bitcoin for noncoders—those trying to understand the inner workings of bitcoin and cryptocurrencies.
Why Are There Bugs on the Cover?
The leafcutter ant is a species that exhibits highly complex behavior in a colony super-organism, but each individual ant operates on a set of simple rules driven by social interaction and the exchange of chemical scents (pheromones). Per Wikipedia: "Next to humans, leafcutter ants form the largest and most complex animal societies on Earth." Leafcutter ants don’t actually eat leaves, but rather use them to farm a fungus, which is the central food source for the colony. Get that? These ants are farming!
Although ants form a caste-based society and have a queen for producing offspring, there is no central authority or leader in an ant colony. The highly intelligent and sophisticated behavior exhibited by a multimillion-member colony is an emergent property from the interaction of the individuals in a social network.
Nature demonstrates that decentralized systems can be resilient and can produce emergent complexity and incredible sophistication without the need for a central authority, hierarchy, or complex parts.
Bitcoin is a highly sophisticated decentralized trust network that can support myriad financial processes. Yet, each node in the bitcoin network follows a few simple mathematical rules. The interaction between many nodes is what leads to the emergence of the sophisticated behavior, not any inherent complexity or trust in any single node. Like an ant colony, the bitcoin network is a resilient network of simple nodes following simple rules that together can do amazing things without any central coordination.
Conventions Used in This Book
The following typographical conventions are used in this book:
- Italic
-
Indicates new terms, URLs, email addresses, filenames, and file extensions.
-
Constant width -
Used for program listings, as well as within paragraphs to refer to program elements such as variable or function names, databases, data types, environment variables, statements, and keywords.
-
Constant width bold -
Shows commands or other text that should be typed literally by the user.
-
Constant width italic -
Shows text that should be replaced with user-supplied values or by values determined by context.
|
Tip
|
This icon signifies a tip or suggestion. |
|
Note
|
This icon signifies a general note. |
|
Warning
|
This icon indicates a warning or caution. |
Code Examples
The examples are illustrated in Python, C++, and using the command line of a Unix-like operating system such as Linux or macOS. All code snippets are available in the GitHub repository in the code subdirectory of the main repo. Fork the book code, try the code examples, or submit corrections via GitHub.
All the code snippets can be replicated on most operating systems with a minimal installation of compilers and interpreters for the corresponding languages. Where necessary, we provide basic installation instructions and step-by-step examples of the output of those instructions.
Some of the code snippets and code output have been reformatted for print. In all such cases, the lines have been split by a backslash (\) character, followed by a newline character. When transcribing the examples, remove those two characters and join the lines again and you should see identical results as shown in the example.
All the code snippets use real values and calculations where possible, so that you can build from example to example and see the same results in any code you write to calculate the same values. For example, the private keys and corresponding public keys and addresses are all real. The sample transactions, blocks, and blockchain references have all been introduced in the actual bitcoin blockchain and are part of the public ledger, so you can review them on any bitcoin system.
Using Code Examples
This book is here to help you get your job done. In general, if example code is offered with this book, you may use it in your programs and documentation. You do not need to contact us for permission unless you’re reproducing a significant portion of the code. For example, writing a program that uses several chunks of code from this book does not require permission. Selling or distributing a CD-ROM of examples from O’Reilly books does require permission. Answering a question by citing this book and quoting example code does not require permission. Incorporating a significant amount of example code from this book into your product’s documentation does require permission.
We appreciate, but do not require, attribution. An attribution usually includes the title, author, publisher, and ISBN. For example: “Mastering Bitcoin by Andreas M. Antonopoulos (O’Reilly). Copyright 2017 Andreas M. Antonopoulos, 978-1-491-95438-6.”
Some editions of this book are offered under an open source license, such as CC-BY-NC, in which case the terms of that license apply.
If you feel your use of code examples falls outside fair use or the permission given above, feel free to contact us at permissions@oreilly.com.
Bitcoin Addresses and Transactions in This Book
The bitcoin addresses, transactions, keys, QR codes, and blockchain data used in this book are, for the most part, real. That means you can browse the blockchain, look at the transactions offered as examples, retrieve them with your own scripts or programs, etc.
However, note that the private keys used to construct addresses are either printed in this book, or have been "burned." That means that if you send money to any of these addresses, the money will either be lost forever, or in some cases everyone who can read the book can take it using the private keys printed in here.
|
Warning
|
DO NOT SEND MONEY TO ANY OF THE ADDRESSES IN THIS BOOK. Your money will be taken by another reader, or lost forever. |
O’Reilly Safari
|
Note
|
Safari (formerly Safari Books Online) is a membership-based training and reference platform for enterprise, government, educators, and individuals. |
Members have access to thousands of books, training videos, Learning Paths, interactive tutorials, and curated playlists from over 250 publishers, including O’Reilly Media, Harvard Business Review, Prentice Hall Professional, Addison-Wesley Professional, Microsoft Press, Sams, Que, Peachpit Press, Adobe, Focal Press, Cisco Press, John Wiley & Sons, Syngress, Morgan Kaufmann, IBM Redbooks, Packt, Adobe Press, FT Press, Apress, Manning, New Riders, McGraw-Hill, Jones & Bartlett, and Course Technology, among others.
For more information, please visit http://oreilly.com/safari.
How to Contact Us
Please address comments and questions concerning this book to the publisher:
- O’Reilly Media, Inc.
- 1005 Gravenstein Highway North
- Sebastopol, CA 95472
- 800-998-9938 (in the United States or Canada)
- 707-829-0515 (international or local)
- 707-829-0104 (fax)
To comment or ask technical questions about this book, send email to bookquestions@oreilly.com.
For more information about our books, courses, conferences, and news, see our website at http://www.oreilly.com.
Find us on Facebook: http://facebook.com/oreilly
Follow us on Twitter: http://twitter.com/oreillymedia
Watch us on YouTube: http://www.youtube.com/oreillymedia
Contacting the Author
You can contact me, Andreas M. Antonopoulos, on my personal site: https://antonopoulos.com/
Information about Mastering Bitcoin as well as the Open Edition and translations are available on: https://bitcoinbook.info/
Follow me on Facebook: https://facebook.com/AndreasMAntonopoulos
Follow me on Twitter: https://twitter.com/aantonop
Follow me on Linkedin: https://linkedin.com/company/aantonop
Many thanks to all my patrons who support my work through monthly donations. You can follow my Patreon page here: https://patreon.com/aantonop
Acknowledgments
This book represents the efforts and contributions of many people. I am grateful for all the help I received from friends, colleagues, and even complete strangers, who joined me in this effort to write the definitive technical book on cryptocurrencies and bitcoin.
It is impossible to make a distinction between the bitcoin technology and the bitcoin community, and this book is as much a product of that community as it is a book on the technology. My work on this book was encouraged, cheered on, supported, and rewarded by the entire bitcoin community from the very beginning until the very end. More than anything, this book has allowed me to be part of a wonderful community for two years and I can’t thank you enough for accepting me into this community. There are far too many people to mention by name—people I’ve met at conferences, events, seminars, meetups, pizza gatherings, and small private gatherings, as well as many who communicated with me by Twitter, on reddit, on bitcointalk.org, and on GitHub who have had an impact on this book. Every idea, analogy, question, answer, and explanation you find in this book was at some point inspired, tested, or improved through my interactions with the community. Thank you all for your support; without you this book would not have happened. I am forever grateful.
The journey to becoming an author starts long before the first book, of course. My first language (and schooling) was Greek, so I had to take a remedial English writing course in my first year of university. I owe thanks to Diana Kordas, my English writing teacher, who helped me build confidence and skills that year. Later, as a professional, I developed my technical writing skills on the topic of data centers, writing for Network World magazine. I owe thanks to John Dix and John Gallant, who gave me my first writing job as a columnist at Network World and to my editor Michael Cooney and my colleague Johna Till Johnson who edited my columns and made them fit for publication. Writing 500 words a week for four years gave me enough experience to eventually consider becoming an author.
Thanks also to those who supported me when I submitted my book proposal to O’Reilly, by providing references and reviewing the proposal. Specifically, thanks to John Gallant, Gregory Ness, Richard Stiennon, Joel Snyder, Adam B. Levine, Sandra Gittlen, John Dix, Johna Till Johnson, Roger Ver, and Jon Matonis. Special thanks to Richard Kagan and Tymon Mattoszko, who reviewed early versions of the proposal and Matthew Taylor, who copyedited the proposal.
Thanks to Cricket Liu, author of the O’Reilly title DNS and BIND, who introduced me to O’Reilly. Thanks also to Michael Loukides and Allyson MacDonald at O’Reilly, who worked for months to help make this book happen. Allyson was especially patient when deadlines were missed and deliverables delayed as life intervened in our planned schedule. For the second edition, I thank Timothy McGovern for guiding the process, Kim Cofer for patiently editing, and Rebecca Panzer for illustrating many new diagrams.
The first few drafts of the first few chapters were the hardest, because bitcoin is a difficult subject to unravel. Every time I pulled on one thread of the bitcoin technology, I had to pull on the whole thing. I repeatedly got stuck and a bit despondent as I struggled to make the topic easy to understand and create a narrative around such a dense technical subject. Eventually, I decided to tell the story of bitcoin through the stories of the people using bitcoin and the whole book became a lot easier to write. I owe thanks to my friend and mentor, Richard Kagan, who helped me unravel the story and get past the moments of writer’s block. I thank Pamela Morgan, who reviewed early drafts of each chapter in the first and second edition of the book, and asked the hard questions to make them better. Also, thanks to the developers of the San Francisco Bitcoin Developers Meetup group as well as Taariq Lewis and Denise Terry for helping test the early material. Thanks also to Andrew Naugler for infographic design.
During the development of the book, I made early drafts available on GitHub and invited public comments. More than a hundred comments, suggestions, corrections, and contributions were submitted in response. Those contributions are explicitly acknowledged, with my thanks, in [github_contrib]. Most of all, my sincere thanks to my volunteer GitHub editors Ming T. Nguyen (1st edition) and Will Binns (2nd edition), who worked tirelessly to curate, manage and resolve pull requests, issue reports, and perform bug fixes on GitHub.
Once the book was drafted, it went through several rounds of technical review. Thanks to Cricket Liu and Lorne Lantz for their thorough review, comments, and support.
Several bitcoin developers contributed code samples, reviews, comments, and encouragement. Thanks to Amir Taaki and Eric Voskuil for example code snippets and many great comments; Chris Kleeschulte for contributing the Bitcore appendix; Vitalik Buterin and Richard Kiss for help with elliptic curve math and code contributions; Gavin Andresen for corrections, comments, and encouragement; Michalis Kargakis for comments, contributions, and btcd writeup; and Robin Inge for errata submissions improving the second print. In the second edition, I again received a lot of help from many Bitcoin Core developers, including Eric Lombrozo who demystified Segregated Witness, Luke-Jr who helped improve the chapter on transactions, Johnson Lau who reviewed Segregated Witness and other chapters, and many others. I owe thanks to Joseph Poon, Tadge Dryja, and Olaoluwa Osuntokun who explained Lightning Network, reviewed my writing, and answered questions when I got stuck.
I owe my love of words and books to my mother, Theresa, who raised me in a house with books lining every wall. My mother also bought me my first computer in 1982, despite being a self-described technophobe. My father, Menelaos, a civil engineer who just published his first book at 80 years old, was the one who taught me logical and analytical thinking and a love of science and engineering.
Thank you all for supporting me throughout this journey.
Early Release Draft (GitHub Contributions)
Many contributors offered comments, corrections, and additions to the early-release draft on GitHub. Thank you all for your contributions to this book.
Following is a list of notable GitHub contributors, including their GitHub ID in parentheses:
-
Alex Waters (alexwaters)
-
Andrew Donald Kennedy (grkvlt)
-
bitcoinctf
-
Bryan Gmyrek (physicsdude)
-
Casey Flynn (cflynn07)
-
Chapman Shoop (belovachap)
-
Christie D’Anna (avocadobreath)
-
Cody Scott (Siecje)
-
coinradar
-
Cragin Godley (cgodley)
-
dallyshalla
-
Diego Viola (diegoviola)
-
Dirk Jäckel (biafra23)
-
Dimitris Tsapakidis (dimitris-t)
-
Dmitry Marakasov (AMDmi3)
-
drstrangeM
-
Ed Eykholt (edeykholt)
-
Ed Leafe (EdLeafe)
-
Edward Posnak (edposnak)
-
Elias Rodrigues (elias19r)
-
Eric Voskuil (evoskuil)
-
Eric Winchell (winchell)
-
Erik Wahlström (erikwam)
-
effectsToCause (vericoin)
-
Esteban Ordano (eordano)
-
ethers
-
fabienhinault
-
Frank Höger (francyi)
-
Gaurav Rana (bitcoinsSG)
-
genjix
-
halseth
-
Holger Schinzel (schinzelh)
-
Ioannis Cherouvim (cherouvim)
-
Ish Ot Jr. (ishotjr)
-
James Addison (jayaddison)
-
Jameson Lopp (jlopp)
-
Jason Bisterfeldt (jbisterfeldt)
-
Javier Rojas (fjrojasgarcia)
-
Jeremy Bokobza (bokobza)
-
JerJohn15
-
Joe Bauers (joebauers)
-
joflynn
-
Johnson Lau (jl2012)
-
Jonathan Cross (jonathancross)
-
Jorgeminator
-
Kai Bakker (kaibakker)
-
Mai-Hsuan Chia (mhchia)
-
Marzig (marzig76)
-
Maximilian Reichel (phramz)
-
Michalis Kargakis (kargakis)
-
Michael C. Ippolito (michaelcippolito)
-
Mihail Russu (MihailRussu)
-
Minh T. Nguyen (enderminh)
-
Nagaraj Hubli (nagarajhubli)
-
Nekomata (nekomata-3)
-
Robert Furse (Rfurse)
-
Richard Kiss (richardkiss)
-
Ruben Alexander (hizzvizz)
-
Sam Ritchie (sritchie)
-
Sergej Kotliar (ziggamon)
-
Seiichi Uchida (topecongiro)
-
Simon de la Rouviere (simondlr)
-
Stephan Oeste (Emzy)
-
takaya-imai
-
Thiago Arrais (thiagoarrais)
-
venzen
-
Will Binns (wbnns)
-
wintercooled
-
wjx
-
Wojciech Langiewicz (wlk)
-
yurigeorgiev4
Quick Glossary
This quick glossary contains many of the terms used in relation to bitcoin. These terms are used throughout the book, so bookmark this for a quick reference.
- address
-
A bitcoin address looks like
1DSrfJdB2AnWaFNgSbv3MZC2m74996JafV. It consists of a string of letters and numbers. It’s really an encoded base58check version of a public key 160-bit hash. Just like you ask others to send an email to your email address, you would ask others to send you bitcoin to one of your bitcoin addresses. - bip
-
Bitcoin Improvement Proposals. A set of proposals that members of the bitcoin community have submitted to improve bitcoin. For example, BIP-21 is a proposal to improve the bitcoin uniform resource identifier (URI) scheme.
- bitcoin
-
The name of the currency unit (the coin), the network, and the software.
- block
-
A grouping of transactions, marked with a timestamp, and a fingerprint of the previous block. The block header is hashed to produce a proof of work, thereby validating the transactions. Valid blocks are added to the main blockchain by network consensus.
- blockchain
-
A list of validated blocks, each linking to its predecessor all the way to the genesis block.
- Byzantine Generals Problem
-
A reliable computer system must be able to cope with the failure of one or more of its components. A failed component may exhibit a type of behavior that is often overlooked—namely, sending conflicting information to different parts of the system. The problem of coping with this type of failure is expressed abstractly as the Byzantine Generals Problem.
- coinbase
-
A special field used as the sole input for coinbase transactions. The coinbase allows claiming the block reward and provides up to 100 bytes for arbitrary data. Not to be confused with Coinbase transaction.
- coinbase transaction
-
The first transaction in a block. Always created by a miner, it includes a single coinbase. Not to be confused with Coinbase.
- cold storage
-
Refers to keeping a reserve of bitcoin offline. Cold storage is achieved when Bitcoin private keys are created and stored in a secure offline environment. Cold storage is important for anyone with bitcoin holdings. Online computers are vulnerable to hackers and should not be used to store a significant amount of bitcoin.
- Colored coins
-
It’s an open source Bitcoin 2.0 protocol that enables developers to create digital assets on top of Bitcoin Blockchain utilizing its functionalities beyond currency.
- confirmations
-
Once a transaction is included in a block, it has one confirmation. As soon as another block is mined on the same blockchain, the transaction has two confirmations, and so on. Six or more confirmations is considered sufficient proof that a transaction cannot be reversed.
- consensus
-
When several nodes, usually most nodes on the network, all have the same blocks in their locally-validated best block chain. Not to be confused with consensus rules.
- consensus rules
-
The block validation rules that full nodes follow to stay in consensus with other nodes. Not to be confused with consensus.
- difficulty
-
A network-wide setting that controls how much computation is required to produce a proof of work.
- difficulty retargeting
-
A network-wide recalculation of the difficulty that occurs once every 2,016 blocks and considers the hashing power of the previous 2,016 blocks.
- difficulty target
-
A difficulty at which all the computation in the network will find blocks approximately every 10 minutes.
- Double spending
-
Double-spending is the result of successfully spending some money more than once. Bitcoin protects against double spending by verifying each transaction added to the block chain to ensure that the inputs for the transaction had not previously already been spent.
- ECDSA
-
Elliptic Curve Digital Signature Algorithm or ECDSA is a cryptographic algorithm used by Bitcoin to ensure that funds can only be spent by their rightful owners.
- Extra Nonce
-
As difficulty increased, miners often cycled through all 4 billion values of the nonce without finding a block. Because the coinbase script can store between 2 and 100 bytes of data, miners started using that space as extra nonce space, allowing them to explore a much larger range of block header values to find valid blocks. "Extra Nonce")
- fees
-
The sender of a transaction often includes a fee to the network for processing the requested transaction. Most transactions require a minimum fee of 0.5 mBTC.
- fork
-
Fork, also known as accidental fork, occurs when two or more blocks have the same block height, forking the block chain. Typically occurs when two or more miners find blocks at nearly the same time. Can also happen as part of an attack.
- genesis block
-
The first block in the blockchain, used to initialize the cryptocurrency.
- Hard Fork
-
Hard Fork, also known as Hard-Forking Change, is a permanent divergence in the blockchain, commonly occurs when non-upgraded nodes can’t validate blocks created by upgraded nodes that follow newer consensus rules. Not to be confused with Fork, Soft fork, Software fork or Git fork.
- Hardware Wallet
-
A hardware Wallet is a special type of bitcoin wallet which stores the user’s private keys in a secure hardware device.
- hash
-
A digital fingerprint of some binary input.
- hashlocks
-
A Hashlock is a type of encumbrance that restricts the spending of an output until a specified piece of data is publicly revealed. Hashlocks have the useful property that once any hashlock is opened publicly, any other hashlock secured using the same key can also be opened. This makes it possible to create multiple outputs that are all encumbered by the same hashlock and which all become spendable at the same time.
- HD Protocol
-
The Hierarchical Deterministic (HD) key creation and transfer protocol (BIP32), which allows creating child keys from parent keys in a hierarchy.
- HD Wallet
-
Wallets using the Hierarchical Deterministic (HD Protocol) key creation and transfer protocol (BIP32).
- HD Wallet Seed
-
HD Wallet Seed or Root Seed is a potentially-short value used as a seed to generate the master private key and master chain code for an HD wallet.
- HTLC
-
A Hashed TimeLock Contract or HTLC is a class of payments that use hashlocks and timelocks to require that the receiver of a payment either acknowledge receiving the payment prior to a deadline by generating cryptographic proof of payment or forfeit the ability to claim the payment, returning it to the payer.
- KYC
-
Know your customer (KYC) is the process of a business, identifying and verifying the identity of its clients. The term is also used to refer to the bank regulation which governs these activities.
- LevelDB
-
LevelDB is an open source on-disk key-value store. LevelDB is a light-weight, single-purpose library for persistence with bindings to many platforms.
- Lightning networks
-
Lightning Network is a proposed implementation of Hashed Timelock Contracts (HTLCs) with bi-directional payment channels which allows payments to be securely routed across multiple peer-to-peer payment channels. This allows the formation of a network where any peer on the network can pay any other peer even if they don’t directly have a channel open between each other.
- Locktime
-
Locktime, or more technically nLockTime, is the part of a transaction which indicates the earliest time or earliest block when that transaction may be added to the block chain.
- mempool
-
The bitcoin Mempool (memory pool) is a collection of all transaction data in a block that have been verified by bitcoin nodes, but are not yet confirmed.
- Merkle Root
-
The root node of a merkle tree, a descendant of all the hashed pairs in the tree. Block headers must include a valid merkle root descended from all transactions in that block.
- Merkle Tree
-
A tree constructed by hashing paired data (the leaves), then pairing and hashing the results until a single hash remains, the merkle root. In Bitcoin, the leaves are almost always transactions from a single block.
- miner
-
A network node that finds valid proof of work for new blocks, by repeated hashing.
- Multisignature
-
Multisignature (multisig) refers to requiring more than one key to authorize a Bitcoin transaction.
- network
-
A peer-to-peer network that propagates transactions and blocks to every bitcoin node on the network.
- Nonce
-
The "nonce" in a Bitcoin block is a 32-bit (4-byte) field whose value is set so that the hash of the block will contain a run of leading zeros. The rest of the fields may not be changed, as they have a defined meaning.
- Off-Chain Transactions
-
An off-chain transaction is the movement of value outside of the block chain. While an on-chain transaction - usually referred to as simply a transaction - modifies the blockchain and depends on the blockchain to determine its validity an off-chain transaction relies on other methods to record and validate the transaction.
- Opcode
-
Operation codes from the Bitcoin Script language which push data or perform functions within a pubkey script or signature script.
- Open Assets Protocol
-
The Open Assets Protocol is a simple and powerful protocol built on top of the Bitcoin Blockchain. It allows issuance and transfer of user-created assets. The Open Assets Protocol is an evolution of the concept of colored coins.
- OP_RETURN
-
An opcode used in one of the outputs in an OP_RETURN transaction. Not to be confused with OP_RETURN transaction.
- OP_RETURN transaction
-
A transaction type relayed and mined by default in Bitcoin Core 0.9.0 and later that adds arbitrary data to a provably unspendable pubkey script that full nodes don’t have to store in their UTXO database. Not to be confused with OP_RETURN opcode.
- Orphan Block
-
Blocks whose parent block has not been processed by the local node, so they can’t be fully validated yet.
- Orphan Transactions
-
Transactions that can’t go into the pool due to one or more missing input transactions.
- Output
-
Output, Transaction Output or TxOut is an output in a transaction which contains two fields: a value field for transferring zero or more satoshis and a pubkey script for indicating what conditions must be fulfilled for those satoshis to be further spent.
- P2PKH
-
Transactions that pay a bitcoin address contain P2PKH or Pay To PubKey Hash scripts. An output locked by a P2PKH script can be unlocked (spent) by presenting a public key and a digital signature created by the corresponding private key.
- P2SH
-
P2SH or Pay To Script Hash is a powerful new type of transaction that greatly simplifies the use of complex transaction scripts. With P2SH the complex script that details the conditions for spending the output (redeem script) is not presented in the locking script. Instead, only a hash of it is in the locking script.
- P2SH address
-
P2SH addresses are Base58Check encodings of the 20-byte hash of a script, P2SH addresses use the version prefix "5", which results in Base58Check-encoded addresses that start with a "3". P2SH addresses hide all of the complexity, so that the person making a payment does not see the script.
- P2WPKH
-
The signature of a P2WPKH (Pay to Witness Public Key Hash) contains the same information as a P2PKH spending, but is located in the witness field instead of the scriptSig field. The scriptPubKey is also modified.
- P2WSH
-
The difference between P2SH and P2WSH (Pay to Witness Script Hash) is about the cryptographic proof location change from the scriptSig field to the witness field and the scriptPubKey that is also modified.
- Paper wallet
-
In the most specific sense, a paper wallet is a document containing all of the data necessary to generate any number of Bitcoin private keys, forming a wallet of keys. However, people often use the term to mean any way of storing bitcoin offline as a physical document. This second definition also includes paper keys and redeemable codes.
- Payment channels
-
A Micropayment Channel or Payment Channel is class of techniques designed to allow users to make multiple Bitcoin transactions without committing all of the transactions to the Bitcoin block chain. In a typical payment channel, only two transactions are added to the block chain but an unlimited or nearly unlimited number of payments can be made between the participants.
- Pooled mining
-
Pooled mining is a mining approach where multiple generating clients contribute to the generation of a block, and then split the block reward according the contributed processing power.
- Proof-of-stake
-
Proof-of-stake (PoS) is a method by which a cryptocurrency blockchain network aims to achieve distributed consensus. Proof of stake asks users to prove ownership of a certain amount of currency (their "stake" in the currency).
- Proof-Of-Work
-
A piece of data that requires significant computation to find. In bitcoin, miners must find a numeric solution to the SHA256 algorithm that meets a network-wide target, the difficulty target.
- reward
-
An amount included in each new block as a reward by the network to the miner who found the Proof-Of-Work solution. It is currently 12.5BTC per block.
- RIPEMD-160
-
RIPEMD-160 is a 160-bit cryptographic hash function. RIPEMD-160 is a strengthened version of RIPEMD with a 160-bit hash result, and is expected to be secure for the next ten years or more.
- Satoshi Nakamoto
-
Satoshi Nakamoto is the name used by the person or people who designed Bitcoin and created its original reference implementation, Bitcoin Core. As a part of the implementation, they also devised the first blockchain database. In the process they were the first to solve the double spending problem for digital currency. Their real identity remains unknown.
- Script
-
Bitcoin uses a scripting system for transactions. Forth-like, Script is simple, stack-based, and processed from left to right. It is purposefully not Turing-complete, with no loops.
- ScriptPubKey (aka Pubkey Script)
-
ScriptPubKey or Pubkey Script, is a script included in outputs which sets the conditions that must be fulfilled for those satoshis to be spent. Data for fulfilling the conditions can be provided in a signature script.
- ScriptSig (aka Signature Script)
-
ScriptSig or Signature Script, is the data generated by a spender which is almost always used as variables to satisfy a pubkey script.
- secret key (aka private key)
-
The secret number that unlocks bitcoin sent to the corresponding address. A secret key looks like
5J76sF8L5jTtzE96r66Sf8cka9y44wdpJjMwCxR3tzLh3ibVPxh. - Segregated Witness
-
Segregated Witness is a proposed upgrade to the Bitcoin protocol which technological innovation separates signature data from Bitcoin transactions. Segregated Witness is a proposed soft fork; a change that technically makes Bitcoin’s protocol rules more restrictive.
- SHA
-
The Secure Hash Algorithm or SHA is a family of cryptographic hash functions published by the National Institute of Standards and Technology (NIST).
- Soft Fork
-
Soft Fork or Soft-Forking Change is a temporary fork in the Blockchain which commonly occurs when miners using non-upgraded nodes don’t follow a new consensus rule their nodes don’t know about. Not to be confused with Fork, Hard fork, Software fork or Git fork.
- SPV (aka Simplified Payment Verification)
-
SPV or Simplified Payment Verification is a method for verifying particular transactions were included in a block without downloading the entire block. The method is used by some lightweight Bitcoin clients.
- Stale Block
-
Block which were successfully mined but which isn’t included on the current best block chain, likely because some other block at the same height had its chain extended first.
- timelocks
-
A Timelock is a type of encumbrance that restricts the spending of some bitcoin until a specified future time or block height. Timelocks feature prominently in many Bitcoin contracts, including payment channels and hashed timelock contracts.
- transaction
-
In simple terms, a transfer of bitcoin from one address to another. More precisely, a transaction is a signed data structure expressing a transfer of value. Transactions are transmitted over the bitcoin network, collected by miners, and included into blocks, made permanent on the blockchain.
- Transaction Pool
-
An unordered collection of transactions that are not in blocks in the main chain, but for which we have input transactions.
- Turing completeness
-
A program language is called "Turing complete", if that it can run any program that a Turing machine can run given enough time and memory.
- UTXO (aka Unspent Transaction Output)
-
UTXO is an Unspent Transaction Output that can be spent as an input in a new transaction.
- wallet
-
Software that holds all your bitcoin addresses and secret keys. Use it to send, receive, and store your bitcoin.
- WIF (aka Wallet Import Format)
-
WIF or Wallet Import Format is a data interchange format designed to allow exporting and importing a single private key with a flag indicating whether or not it uses a compressed public key.
Introduction
What Is Bitcoin?
Bitcoin is a collection of concepts and technologies that form the basis of a digital money ecosystem. Units of currency called bitcoin are used to store and transmit value among participants in the bitcoin network. Bitcoin users communicate with each other using the bitcoin protocol primarily via the internet, although other transport networks can also be used. The bitcoin protocol stack, available as open source software, can be run on a wide range of computing devices, including laptops and smartphones, making the technology easily accessible.
Users can transfer bitcoin over the network to do just about anything that can be done with conventional currencies, including buy and sell goods, send money to people or organizations, or extend credit. Bitcoin can be purchased, sold, and exchanged for other currencies at specialized currency exchanges. Bitcoin in a sense is the perfect form of money for the internet because it is fast, secure, and borderless.
Unlike traditional currencies, bitcoin are entirely virtual. There are no physical coins or even digital coins per se. The coins are implied in transactions that transfer value from sender to recipient. Users of bitcoin own keys that allow them to prove ownership of bitcoin in the bitcoin network. With these keys they can sign transactions to unlock the value and spend it by transferring it to a new owner. Keys are often stored in a digital wallet on each user’s computer or smartphone. Possession of the key that can sign a transaction is the only prerequisite to spending bitcoin, putting the control entirely in the hands of each user.
Bitcoin is a distributed, peer-to-peer system. As such there is no "central" server or point of control. Bitcoin are created through a process called "mining," which involves competing to find solutions to a mathematical problem while processing bitcoin transactions. Any participant in the bitcoin network (i.e., anyone using a device running the full bitcoin protocol stack) may operate as a miner, using their computer’s processing power to verify and record transactions. Every 10 minutes, on average, someone is able to validate the transactions of the past 10 minutes and is rewarded with brand new bitcoin. Essentially, bitcoin mining decentralizes the currency-issuance and clearing functions of a central bank and replaces the need for any central bank.
The bitcoin protocol includes built-in algorithms that regulate the mining function across the network. The difficulty of the processing task that miners must perform is adjusted dynamically so that, on average, someone succeeds every 10 minutes regardless of how many miners (and how much processing) are competing at any moment. The protocol also halves the rate at which new bitcoin are created every 4 years, and limits the total number of bitcoin that will be created to a fixed total just below 21 million coins. The result is that the number of bitcoin in circulation closely follows an easily predictable curve that approaches 21 million by the year 2140. Due to bitcoin’s diminishing rate of issuance, over the long term, the bitcoin currency is deflationary. Furthermore, bitcoin cannot be inflated by "printing" new money above and beyond the expected issuance rate.
Behind the scenes, bitcoin is also the name of the protocol, a peer-to-peer network, and a distributed computing innovation. The bitcoin currency is really only the first application of this invention. Bitcoin represents the culmination of decades of research in cryptography and distributed systems and includes four key innovations brought together in a unique and powerful combination. Bitcoin consists of:
-
A decentralized peer-to-peer network (the bitcoin protocol)
-
A public transaction ledger (the blockchain)
-
A set of rules for independent transaction validation and currency issuance (consensus rules)
-
A mechanism for reaching global decentralized consensus on the valid blockchain (Proof-of-Work algorithm)
As a developer, I see bitcoin as akin to the internet of money, a network for propagating value and securing the ownership of digital assets via distributed computation. There’s a lot more to bitcoin than first meets the eye.
In this chapter we’ll get started by explaining some of the main concepts and terms, getting the necessary software, and using bitcoin for simple transactions. In following chapters we’ll start unwrapping the layers of technology that make bitcoin possible and examine the inner workings of the bitcoin network and protocol.
History of Bitcoin
Bitcoin was invented in 2008 with the publication of a paper titled "Bitcoin: A Peer-to-Peer Electronic Cash System,"
["Bitcoin: A Peer-to-Peer Electronic Cash System," Satoshi Nakamoto (https://bitcoin.org/bitcoin.pdf).]
written under the alias of Satoshi Nakamoto (see [satoshi_whitepaper]). Nakamoto combined several prior inventions such as b-money and HashCash to create a completely decentralized electronic cash system that does not rely on a central authority for currency issuance or settlement and validation of transactions. The key innovation was to use a distributed computation system (called a "Proof-of-Work" algorithm) to conduct a global "election" every 10 minutes, allowing the decentralized network to arrive at consensus about the state of transactions. This elegantly solves the issue of double-spend where a single currency unit can be spent twice. Previously, the double-spend problem was a weakness of digital currency and was addressed by clearing all transactions through a central clearinghouse.
The bitcoin network started in 2009, based on a reference implementation published by Nakamoto and since revised by many other programmers. The implementation of the Proof-of-Work algorithm (mining) that provides security and resilience for bitcoin has increased in power exponentially, and now exceeds the combined processing power of the world’s top supercomputers. Bitcoin’s total market value has at times exceeded $20 billion US dollars, depending on the bitcoin-to-dollar exchange rate. The largest transaction processed so far by the network was $150 million US dollars, transmitted instantly and processed without any fees.
Satoshi Nakamoto withdrew from the public in April 2011, leaving the responsibility of developing the code and network to a thriving group of volunteers. The identity of the person or people behind bitcoin is still unknown. However, neither Satoshi Nakamoto nor anyone else exerts individual control over the bitcoin system, which operates based on fully transparent mathematical principles, open source code, and consensus among participants. The invention itself is groundbreaking and has already spawned new science in the fields of distributed computing, economics, and econometrics.
Bitcoin Uses, Users, and Their Stories
Bitcoin is an innovation in the ancient technology of money. At its core, money simply facilitates the exchange of value between people. Therefore, in order to fully understand bitcoin and its uses, we’ll examine it from the perspective of people using it. Each of the people and their stories, as listed here, illustrates one or more specific use cases. We’ll be seeing them throughout the book:
- North American low-value retail
-
Alice lives in Northern California’s Bay Area. She has heard about bitcoin from her techie friends and wants to start using it. We will follow her story as she learns about bitcoin, acquires some, and then spends some of her bitcoin to buy a cup of coffee at Bob’s Cafe in Palo Alto. This story will introduce us to the software, the exchanges, and basic transactions from the perspective of a retail consumer.
- North American high-value retail
-
Carol is an art gallery owner in San Francisco. She sells expensive paintings for bitcoin. This story will introduce the risks of a "51%" consensus attack for retailers of high-value items.
- Offshore contract services
-
Bob, the cafe owner in Palo Alto, is building a new website. He has contracted with an Indian web developer, Gopesh, who lives in Bangalore, India. Gopesh has agreed to be paid in bitcoin. This story will examine the use of bitcoin for outsourcing, contract services, and international wire transfers.
- Web store
-
Gabriel is an enterprising young teenager in Rio de Janeiro, running a small web store that sells bitcoin-branded t-shirts, coffee mugs, and stickers. Gabriel is too young to have a bank account, but his parents are encouraging his entrepreneurial spirit.
- Charitable donations
-
Eugenia is the director of a children’s charity in the Philippines. Recently she has discovered bitcoin and wants to use it to reach a whole new group of foreign and domestic donors to fundraise for her charity. She’s also investigating ways to use bitcoin to distribute funds quickly to areas of need. This story will show the use of bitcoin for global fundraising across currencies and borders and the use of an open ledger for transparency in charitable organizations.
- Import/export
-
Mohammed is an electronics importer in Dubai. He’s trying to use bitcoin to buy electronics from the United States and China for import into the UAE to accelerate the process of payments for imports. This story will show how bitcoin can be used for large business-to-business international payments tied to physical goods.
- Mining for bitcoin
-
Jing is a computer engineering student in Shanghai. He has built a "mining" rig to mine for bitcoin using his engineering skills to supplement his income. This story will examine the "industrial" base of bitcoin: the specialized equipment used to secure the bitcoin network and issue new currency.
Each of these stories is based on the real people and real industries currently using bitcoin to create new markets, new industries, and innovative solutions to global economic issues.
Getting Started
Bitcoin is a protocol that can be accessed using a client application that speaks the protocol. A "bitcoin wallet" is the most common user interface to the bitcoin system, just like a web browser is the most common user interface for the HTTP protocol. There are many implementations and brands of bitcoin wallets, just like there are many brands of web browsers (e.g., Chrome, Safari, Firefox, and Internet Explorer). And just like we all have our favorite browsers (Mozilla Firefox, Yay!) and our villains (Internet Explorer, Yuck!), bitcoin wallets vary in quality, performance, security, privacy, and reliability. There is also a reference implementation of the bitcoin protocol that includes a wallet, known as the "Satoshi Client" or "Bitcoin Core," which is derived from the original implementation written by Satoshi Nakamoto.
Choosing a Bitcoin Wallet
Bitcoin wallets are one of the most actively developed applications in the bitcoin ecosystem. There is intense competition, and while a new wallet is probably being developed right now, several wallets from last year are no longer actively maintained. Many wallets focus on specific platforms or specific uses and some are more suitable for beginners while others are filled with features for advanced users. Choosing a wallet is highly subjective and depends on the use and user expertise. It is therefore impossible to recommend a specific brand or project of wallet. However, we can categorize bitcoin wallets according to their platform and function and provide some clarity about all the different types of wallets that exist. Better yet, moving money between bitcoin wallets is easy, cheap, and fast, so it is worth trying out several different wallets until you find one that fits your needs.
Bitcoin wallets can be categorized as follows, according to the platform:
- Desktop wallet
-
A desktop wallet was the first type of bitcoin wallet created as a reference implementation and many users run desktop wallets for the features, autonomy, and control they offer. Running on general-use operating systems such as Windows and Mac OS has certain security disadvantages however, as these platforms are often insecure and poorly configured.
- Mobile wallet
-
A mobile wallet is the most common type of bitcoin wallet. Running on smart-phone operating systems such as Apple iOS and Android, these wallets are often a great choice for new users. Many are designed for simplicity and ease-of-use, but there are also fully featured mobile wallets for power users.
- Web wallet
-
Web wallets are accessed through a web browser and store the user’s wallet on a server owned by a third party. This is similar to webmail in that it relies entirely on a third-party server. Some of these services operate using client-side code running in the user’s browser, which keeps control of the bitcoin keys in the hands of the user. Most, however, present a compromise by taking control of the bitcoin keys from users in exchange for ease-of-use. It is inadvisable to store large amounts of bitcoin on third-party systems.
- Hardware wallet
-
Hardware wallets are devices that operate a secure self-contained bitcoin wallet on special-purpose hardware. They are operated via USB with a desktop web browser or via near-field-communication (NFC) on a mobile device. By handling all bitcoin-related operations on the specialized hardware, these wallets are considered very secure and suitable for storing large amounts of bitcoin.
- Paper wallet
-
The keys controlling bitcoin can also be printed for long-term storage. These are known as paper wallets even though other materials (wood, metal, etc.) can be used. Paper wallets offer a low-tech but highly secure means of storing bitcoin long term. Offline storage is also often referred to as cold storage.
Another way to categorize bitcoin wallets is by their degree of autonomy and how they interact with the bitcoin network:
- Full-node client
-
A full client, or "full node," is a client that stores the entire history of bitcoin transactions (every transaction by every user, ever), manages users' wallets, and can initiate transactions directly on the bitcoin network. A full node handles all aspects of the protocol and can independently validate the entire blockchain and any transaction. A full-node client consumes substantial computer resources (e.g., more than 125 GB of disk, 2 GB of RAM) but offers complete autonomy and independent transaction verification.
- Lightweight client
-
A lightweight client, also known as a simple-payment-verification (SPV) client, connects to bitcoin full nodes (mentioned previously) for access to the bitcoin transaction information, but stores the user wallet locally and independently creates, validates, and transmits transactions. Lightweight clients interact directly with the bitcoin network, without an intermediary.
- Third-party API client
-
A third-party API client is one that interacts with bitcoin through a third-party system of application programming interfaces (APIs), rather than by connecting to the bitcoin network directly. The wallet may be stored by the user or by third-party servers, but all transactions go through a third party.
Combining these categorizations, many bitcoin wallets fall into a few groups, with the three most common being desktop full client, mobile lightweight wallet, and web third-party wallet. The lines between different categories are often blurry, as many wallets run on multiple platforms and can interact with the network in different ways.
For the purposes of this book, we will be demonstrating the use of a variety of downloadable bitcoin clients, from the reference implementation (Bitcoin Core) to mobile and web wallets. Some of the examples will require the use of Bitcoin Core, which, in addition to being a full client, also exposes APIs to the wallet, network, and transaction services. If you are planning to explore the programmatic interfaces into the bitcoin system, you will need to run Bitcoin Core, or one of the alternative clients (see [alt_libraries]).
Quick Start
Alice, who we introduced in [user-stories], is not a technical user and only recently heard about bitcoin from her friend Joe. While at a party, Joe is once again enthusiastically explaining bitcoin to all around him and is offering a demonstration. Intrigued, Alice asks how she can get started with bitcoin. Joe says that a mobile wallet is best for new users and he recommends a few of his favorite wallets. Alice downloads "Mycelium" for Android and installs it on her phone.
When Alice runs Mycelium for the first time, as with many bitcoin wallets, the application automatically creates a new wallet for her. Alice sees the wallet on her screen, as shown in [mycelium-welcome] (note: do not send bitcoin to this sample address, it will be lost forever).
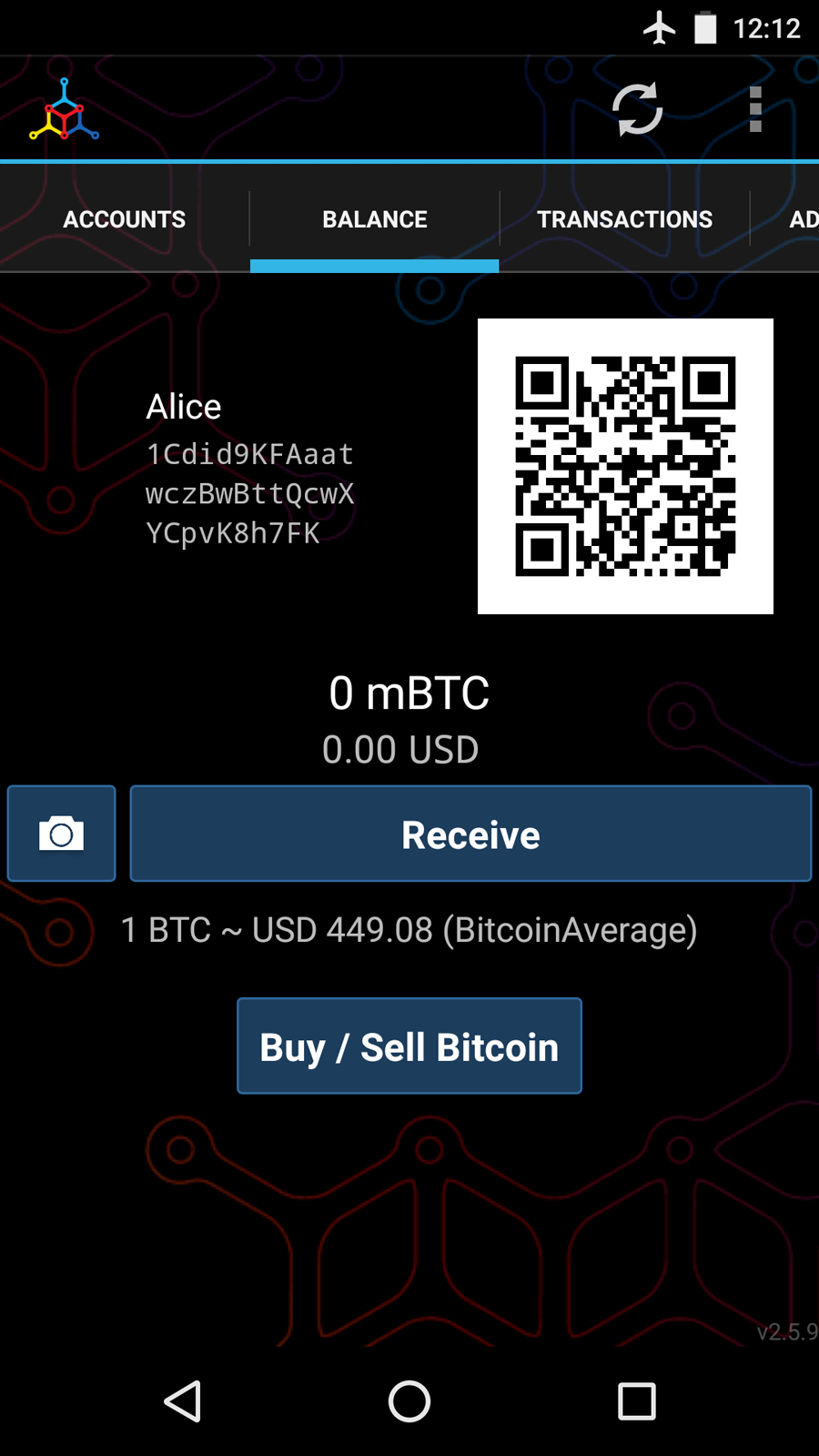
The most important part of this screen is Alice’s bitcoin address. On the screen it appears as a long string of letters and numbers: 1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK. Next to the wallet’s bitcoin address is a QR code, a form of barcode that contains the same information in a format that can be scanned by a smartphone camera. The QR code is the square with a pattern of black and white dots. Alice can copy the bitcoin address or the QR code onto her clipboard by tapping the QR code, or the Receive button. In most wallets, tapping the QR code will also magnify it, so that it can be more easily scanned by a smartphone camera.
|
Tip
|
Bitcoin addresses start with a 1 or 3. Like email addresses, they can be shared with other bitcoin users who can use them to send bitcoin directly to your wallet. There is nothing sensitive, from a security perspective, about the bitcoin address. It can be posted anywhere without risking the security of the account. Unlike email addresses, you can create new addresses as often as you like, all of which will direct funds to your wallet. In fact, many modern wallets automatically create a new address for every transaction to maximize privacy. A wallet is simply a collection of addresses and the keys that unlock the funds within. |
Alice is now ready to receive funds. Her wallet application randomly generated a private key (described in more detail in [private_keys]) together with its corresponding bitcoin address. At this point, her bitcoin address is not known to the bitcoin network or "registered" with any part of the bitcoin system. Her bitcoin address is simply a number that corresponds to a key that she can use to control access to the funds. It was generated independently by her wallet without reference or registration with any service. In fact, in most wallets, there is no association between the bitcoin address and any externally identifiable information including the user’s identity. Until the moment this address is referenced as the recipient of value in a transaction posted on the bitcoin ledger, the bitcoin address is simply part of the vast number of possible addresses that are valid in bitcoin. Only once it has been associated with a transaction does it become part of the known addresses in the network.
Alice is now ready to start using her new bitcoin wallet.
Getting Your First Bitcoin
The first and often most difficult task for new users is to acquire some bitcoin. Unlike other foreign currencies, you cannot yet buy bitcoin at a bank or foreign exchange kiosk.
Bitcoin transactions are irreversible. Most electronic payment networks such as credit cards, debit cards, PayPal, and bank account transfers are reversible. For someone selling bitcoin, this difference introduces a very high risk that the buyer will reverse the electronic payment after they have received bitcoin, in effect defrauding the seller. To mitigate this risk, companies accepting traditional electronic payments in return for bitcoin usually require buyers to undergo identity verification and credit-worthiness checks, which may take several days or weeks. As a new user, this means you cannot buy bitcoin instantly with a credit card. With a bit of patience and creative thinking, however, you won’t need to.
Here are some methods for getting bitcoin as a new user:
-
Find a friend who has bitcoin and buy some from him or her directly. Many bitcoin users start this way. This method is the least complicated. One way to meet people with bitcoin is to attend a local bitcoin meetup listed at Meetup.com.
-
Use a classified service such as localbitcoins.com to find a seller in your area to buy bitcoin for cash in an in-person transaction.
-
Earn bitcoin by selling a product or service for bitcoin. If you are a programmer, sell your programming skills. If you’re a hairdresser, cut hair for bitcoin.
-
Use a bitcoin ATM in your city. A bitcoin ATM is a machine that accepts cash and sends bitcoin to your smartphone bitcoin wallet. Find a bitcoin ATM close to you using an online map from Coin ATM Radar.
-
Use a bitcoin currency exchange linked to your bank account. Many countries now have currency exchanges that offer a market for buyers and sellers to swap bitcoin with local currency. Exchange-rate listing services, such as BitcoinAverage, often show a list of bitcoin exchanges for each currency.
|
Tip
|
One of the advantages of bitcoin over other payment systems is that, when used correctly, it affords users much more privacy. Acquiring, holding, and spending bitcoin does not require you to divulge sensitive and personally identifiable information to third parties. However, where bitcoin touches traditional systems, such as currency exchanges, national and international regulations often apply. In order to exchange bitcoin for your national currency, you will often be required to provide proof of identity and banking information. Users should be aware that once a bitcoin address is attached to an identity, all associated bitcoin transactions are also easy to identify and track. This is one reason many users choose to maintain dedicated exchange accounts unlinked to their wallets. |
Alice was introduced to bitcoin by a friend so she has an easy way to acquire her first bitcoin. Next, we will look at how she buys bitcoin from her friend Joe and how Joe sends the bitcoin to her wallet.
Finding the Current Price of Bitcoin
Before Alice can buy bitcoin from Joe, they have to agree on the exchange rate between bitcoin and US dollars. This brings up a common question for those new to bitcoin: "Who sets the bitcoin price?" The short answer is that the price is set by markets.
Bitcoin, like most other currencies, has a floating exchange rate. That means that the value of bitcoin vis-a-vis any other currency fluctuates according to supply and demand in the various markets where it is traded. For example, the "price" of bitcoin in US dollars is calculated in each market based on the most recent trade of bitcoin and US dollars. As such, the price tends to fluctuate minutely several times per second. A pricing service will aggregate the prices from several markets and calculate a volume-weighted average representing the broad market exchange rate of a currency pair (e.g., BTC/USD).
There are hundreds of applications and websites that can provide the current market rate. Here are some of the most popular:
- Bitcoin Average
-
A site that provides a simple view of the volume-weighted-average for each currency.
- CoinCap
-
A service listing the market capitalization and exchange rates of hundreds of crypto-currencies, including bitcoin.
- Chicago Mercantile Exchange Bitcoin Reference Rate
-
A reference rate that can be used for institutional and contractual reference, provided as part of investment data feeds by the CME.
In addition to these various sites and applications, most bitcoin wallets will automatically convert amounts between bitcoin and other currencies. Joe will use his wallet to convert the price automatically before sending bitcoin to Alice.
Sending and Receiving Bitcoin
Alice has decided to convert $10 US dollars into bitcoin, so as not to risk too much money on this new technology. She gives Joe $10 in cash, opens her Mycelium wallet application, and selects Receive. This displays a QR code with Alice’s first bitcoin address.
Joe then selects Send on his smartphone wallet and is presented with a screen containing two inputs:
-
A destination bitcoin address
-
The amount to send, in bitcoin (BTC) or his local currency (USD)
In the input field for the bitcoin address, there is a small icon that looks like a QR code. This allows Joe to scan the barcode with his smartphone camera so that he doesn’t have to type in Alice’s bitcoin address, which is quite long and difficult to type. Joe taps the QR code icon and activates the smartphone camera, scanning the QR code displayed on Alice’s smartphone.
Joe now has Alice’s bitcoin address set as the recipient. Joe enters the amount as $10 US dollars and his wallet converts it by accessing the most recent exchange rate from an online service. The exchange rate at the time is $100 US dollars per bitcoin, so $10 US dollars is worth 0.10 bitcoin (BTC), or 100 millibitcoin (mBTC) as shown in the screenshot from Joe’s wallet (see [airbitz-mobile-send]).
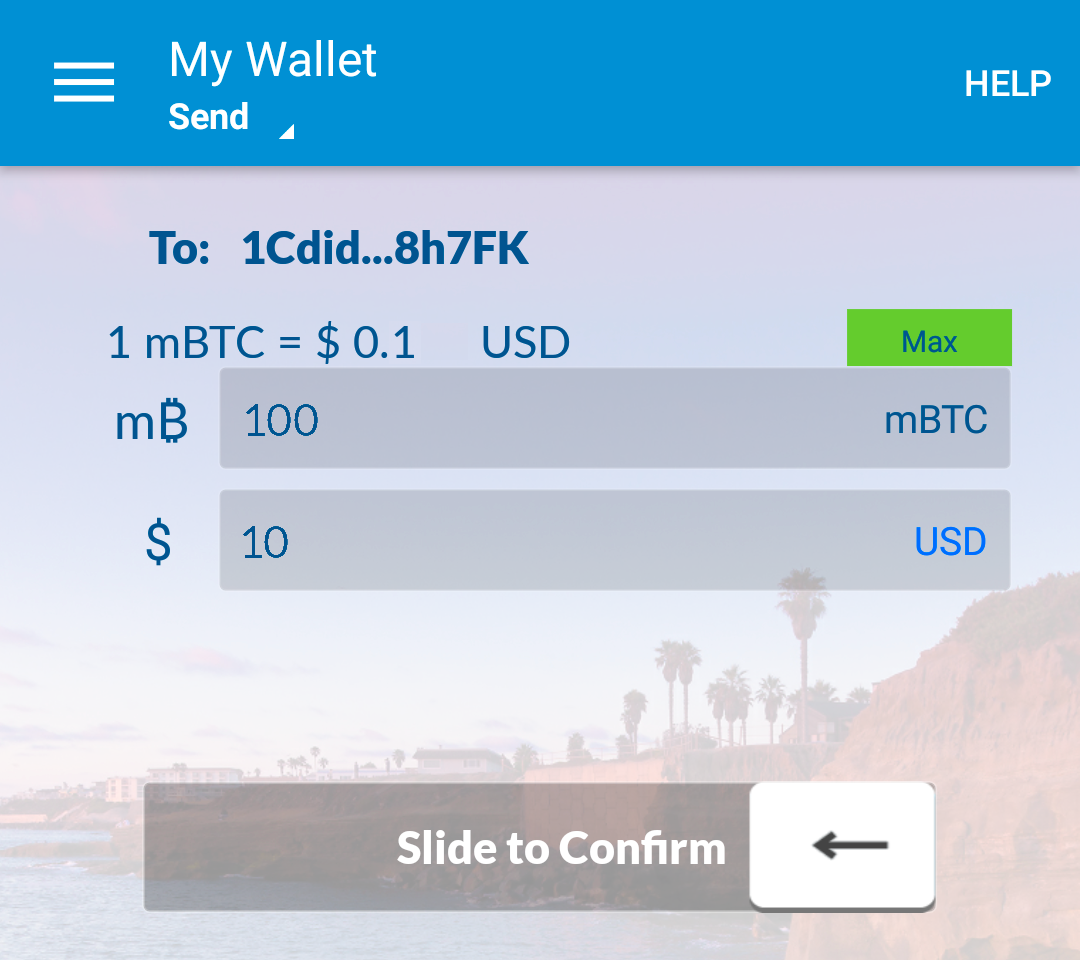
Joe then carefully checks to make sure he has entered the correct amount, because he is about to transmit money and mistakes are irreversible. After double-checking the address and amount, he presses Send to transmit the transaction. Joe’s mobile bitcoin wallet constructs a transaction that assigns 0.10 BTC to the address provided by Alice, sourcing the funds from Joe’s wallet and signing the transaction with Joe’s private keys. This tells the bitcoin network that Joe has authorized a transfer of value to Alice’s new address. As the transaction is transmitted via the peer-to-peer protocol, it quickly propagates across the bitcoin network. In less than a second, most of the well-connected nodes in the network receive the transaction and see Alice’s address for the first time.
Meanwhile, Alice’s wallet is constantly "listening" to published transactions on the bitcoin network, looking for any that match the addresses in her wallets. A few seconds after Joe’s wallet transmits the transaction, Alice’s wallet will indicate that it is receiving 0.10 BTC.
Alice is now the proud owner of 0.10 BTC that she can spend. In the next chapter we will look at her first purchase with bitcoin, and examine the underlying transaction and propagation technologies in more detail.
How Bitcoin Works
Transactions, Blocks, Mining, and the Blockchain
The bitcoin system, unlike traditional banking and payment systems, is based on decentralized trust. Instead of a central trusted authority, in bitcoin, trust is achieved as an emergent property from the interactions of different participants in the bitcoin system. In this chapter, we will examine bitcoin from a high level by tracking a single transaction through the bitcoin system and watch as it becomes "trusted" and accepted by the bitcoin mechanism of distributed consensus and is finally recorded on the blockchain, the distributed ledger of all transactions. Subsequent chapters will delve into the technology behind transactions, the network, and mining.
Bitcoin Overview
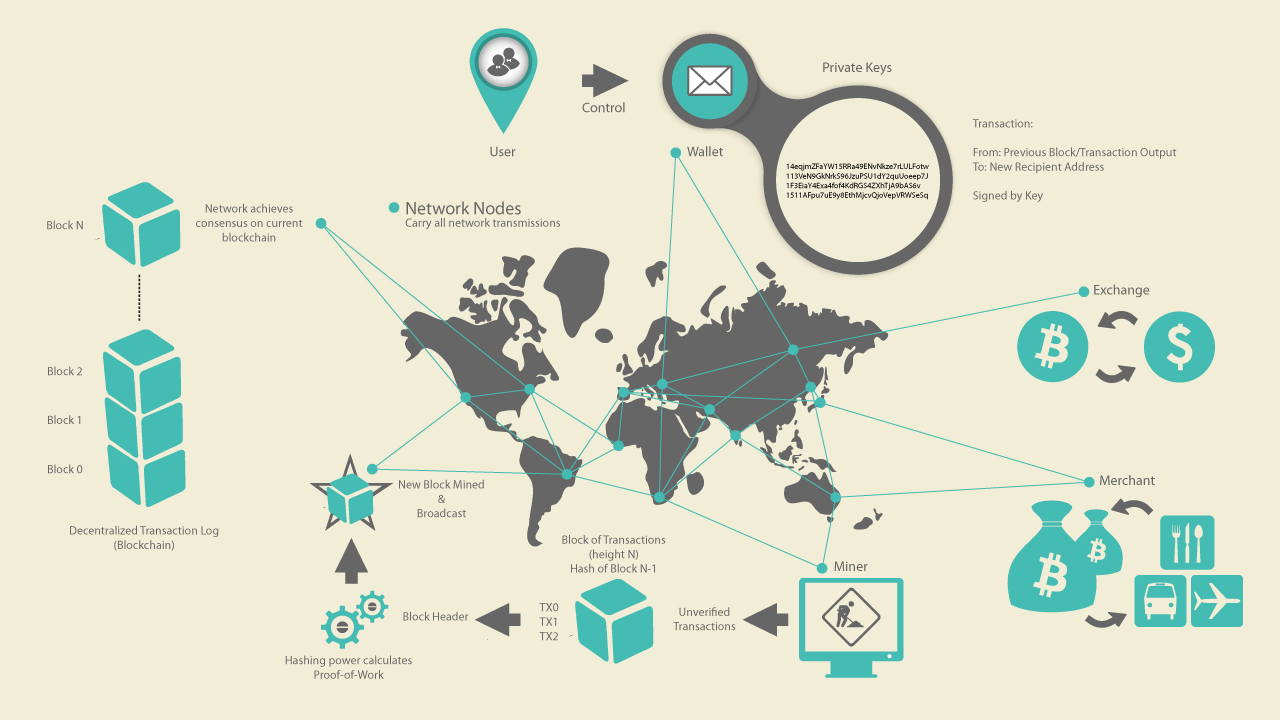
In the overview diagram shown in [bitcoin-overview], we see that the bitcoin system consists of users with wallets containing keys, transactions that are propagated across the network, and miners who produce (through competitive computation) the consensus blockchain, which is the authoritative ledger of all transactions.
Each example in this chapter is based on an actual transaction made on the bitcoin network, simulating the interactions between the users (Joe, Alice, Bob, and Gopesh) by sending funds from one wallet to another. While tracking a transaction through the bitcoin network to the blockchain, we will use a blockchain explorer site to visualize each step. A blockchain explorer is a web application that operates as a bitcoin search engine, in that it allows you to search for addresses, transactions, and blocks and see the relationships and flows between them.
Popular blockchain explorers include:
Each of these has a search function that can take a bitcoin address, transaction hash, block number, or block hash and retrieve corresponding information from the bitcoin network. With each transaction or block example, we will provide a URL so you can look it up yourself and study it in detail.
Buying a Cup of Coffee
Alice, introduced in the previous chapter, is a new user who has just acquired her first bitcoin. In [getting_first_bitcoin], Alice met with her friend Joe to exchange some cash for bitcoin. The transaction created by Joe funded Alice’s wallet with 0.10 BTC. Now Alice will make her first retail transaction, buying a cup of coffee at Bob’s coffee shop in Palo Alto, California.
Bob’s Cafe recently started accepting bitcoin payments by adding a bitcoin option to its point-of-sale system. The prices at Bob’s Cafe are listed in the local currency (US dollars), but at the register, customers have the option of paying in either dollars or bitcoin. Alice places her order for a cup of coffee and Bob enters it into the register, as he does for all transactions. The point-of-sale system automatically converts the total price from US dollars to bitcoin at the prevailing market rate and displays the price in both currencies:
Total:
$1.50 USD
0.015 BTCBob says, "That’s one-dollar-fifty, or fifteen millibits."
Bob’s point-of-sale system will also automatically create a special QR code containing a payment request (see [payment-request-QR]).
Unlike a QR code that simply contains a destination bitcoin address, a payment request is a QR-encoded URL that contains a destination address, a payment amount, and a generic description such as "Bob’s Cafe." This allows a bitcoin wallet application to prefill the information used to send the payment while showing a human-readable description to the user. You can scan the QR code with a bitcoin wallet application to see what Alice would see.

|
Tip
|
Try to scan this with your wallet to see the address and amount but DO NOT SEND MONEY. |
bitcoin:1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA?
amount=0.015&
label=Bob%27s%20Cafe&
message=Purchase%20at%20Bob%27s%20Cafe
Components of the URL
A bitcoin address: "1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA"
The payment amount: "0.015"
A label for the recipient address: "Bob's Cafe"
A description for the payment: "Purchase at Bob's Cafe"Alice uses her smartphone to scan the barcode on display. Her smartphone shows a payment of 0.0150 BTC to Bob’s Cafe and she selects Send to authorize the payment. Within a few seconds (about the same amount of time as a credit card authorization), Bob sees the transaction on the register, completing the transaction.
In the following sections we will examine this transaction in more detail. We’ll see how Alice’s wallet constructed it, how it was propagated across the network, how it was verified, and finally, how Bob can spend that amount in subsequent transactions.
|
Note
|
The bitcoin network can transact in fractional values, e.g., from millibitcoin (1/1000th of a bitcoin) down to 1/100,000,000th of a bitcoin, which is known as a satoshi. Throughout this book we’ll use the term “bitcoin” to refer to any quantity of bitcoin currency, from the smallest unit (1 satoshi) to the total number (21,000,000) of all bitcoin that will ever be mined. |
You can examine Alice’s transaction to Bob’s Cafe on the blockchain using a block explorer site ([view_alice_transaction]):
https://blockexplorer.com/tx/0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2Bitcoin Transactions
In simple terms, a transaction tells the network that the owner of some bitcoin value has authorized the transfer of that value to another owner. The new owner can now spend the bitcoin by creating another transaction that authorizes transfer to another owner, and so on, in a chain of ownership.
Transaction Inputs and Outputs
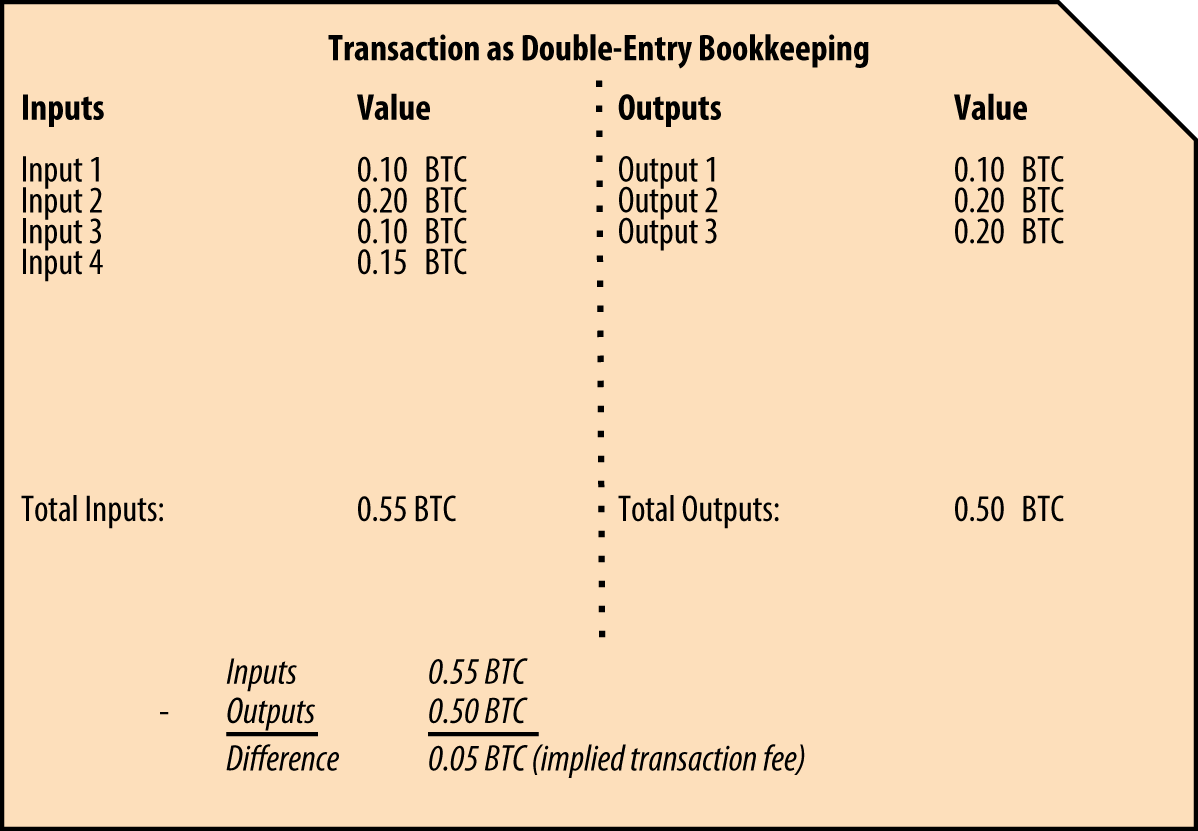
Transactions are like lines in a double-entry bookkeeping ledger. Each transaction contains one or more "inputs," which are like debits against a bitcoin account. On the other side of the transaction, there are one or more "outputs," which are like credits added to a bitcoin account. The inputs and outputs (debits and credits) do not necessarily add up to the same amount. Instead, outputs add up to slightly less than inputs and the difference represents an implied transaction fee, which is a small payment collected by the miner who includes the transaction in the ledger. A bitcoin transaction is shown as a bookkeeping ledger entry in [transaction-double-entry].
The transaction also contains proof of ownership for each amount of bitcoin (inputs) whose value is being spent, in the form of a digital signature from the owner, which can be independently validated by anyone. In bitcoin terms, "spending" is signing a transaction that transfers value from a previous transaction over to a new owner identified by a bitcoin address.
Transaction Chains
Alice’s payment to Bob’s Cafe uses a previous transaction’s output as its input. In the previous chapter, Alice received bitcoin from her friend Joe in return for cash. That transaction created a bitcoin value locked by Alice’s key. Her new transaction to Bob’s Cafe references the previous transaction as an input and creates new outputs to pay for the cup of coffee and receive change. The transactions form a chain, where the inputs from the latest transaction correspond to outputs from previous transactions. Alice’s key provides the signature that unlocks those previous transaction outputs, thereby proving to the bitcoin network that she owns the funds. She attaches the payment for coffee to Bob’s address, thereby "encumbering" that output with the requirement that Bob produces a signature in order to spend that amount. This represents a transfer of value between Alice and Bob. This chain of transactions, from Joe to Alice to Bob, is illustrated in [blockchain-mnemonic].
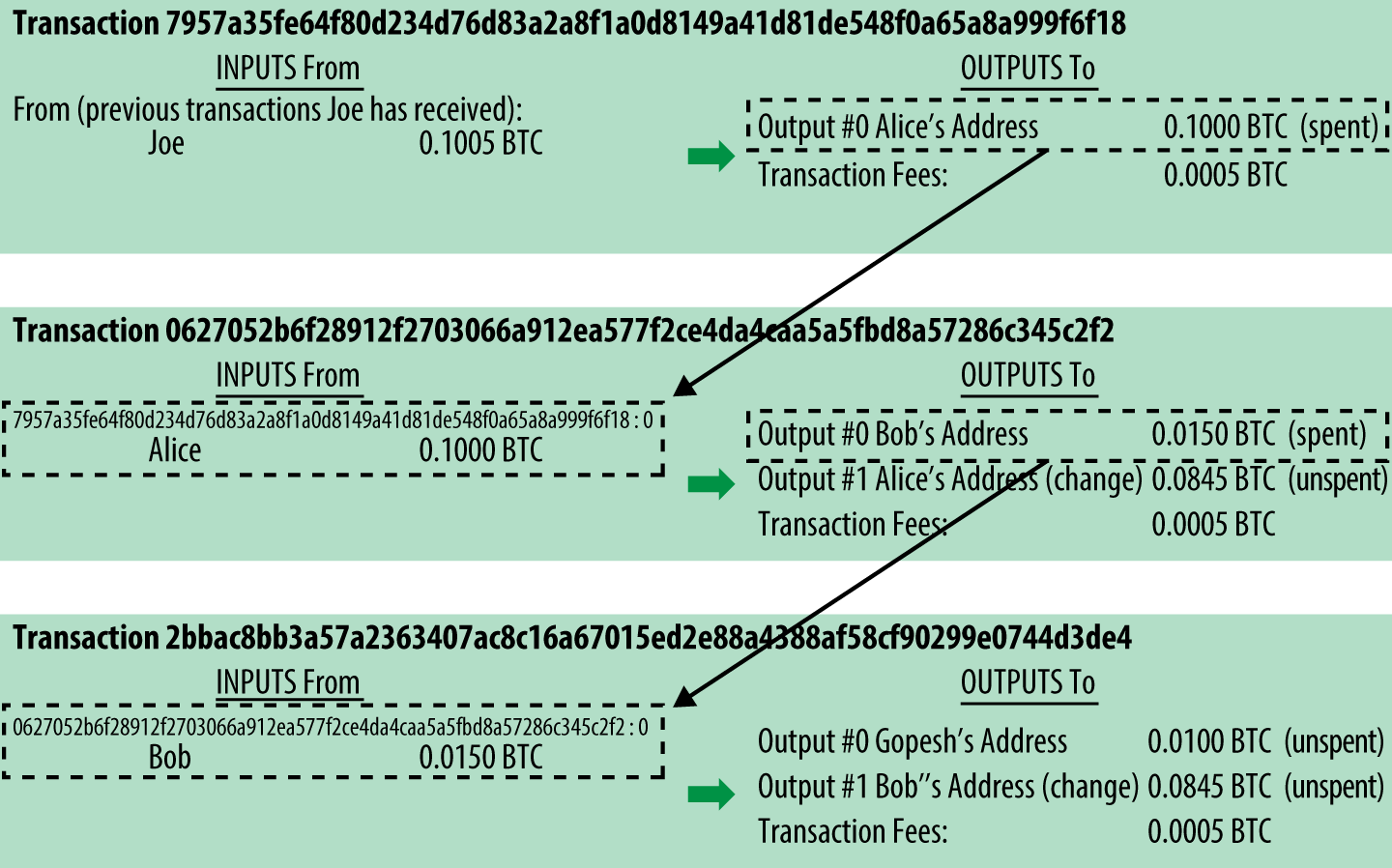
Making Change
Many bitcoin transactions will include outputs that reference both an address of the new owner and an address of the current owner, called the change address. This is because transaction inputs, like currency notes, cannot be divided. If you purchase a $5 US dollar item in a store but use a $20 US dollar bill to pay for the item, you expect to receive $15 US dollars in change. The same concept applies with bitcoin transaction inputs. If you purchased an item that costs 5 bitcoin but only had a 20 bitcoin input to use, you would send one output of 5 bitcoin to the store owner and one output of 15 bitcoin back to yourself as change (less any applicable transaction fee). Importantly, the change address does not have to be the same address as that of the input and for privacy reasons is often a new address from the owner’s wallet.
Different wallets may use different strategies when aggregating inputs to make a payment requested by the user. They might aggregate many small inputs, or use one that is equal to or larger than the desired payment. Unless the wallet can aggregate inputs in such a way to exactly match the desired payment plus transaction fees, the wallet will need to generate some change. This is very similar to how people handle cash. If you always use the largest bill in your pocket, you will end up with a pocket full of loose change. If you only use the loose change, you’ll always have only big bills. People subconsciously find a balance between these two extremes, and bitcoin wallet developers strive to program this balance.
In summary, transactions move value from transaction inputs to transaction outputs. An input is a reference to a previous transaction’s output, showing where the value is coming from. A transaction output directs a specific value to a new owner’s bitcoin address and can include a change output back to the original owner. Outputs from one transaction can be used as inputs in a new transaction, thus creating a chain of ownership as the value is moved from owner to owner (see [blockchain-mnemonic]).
Common Transaction Forms
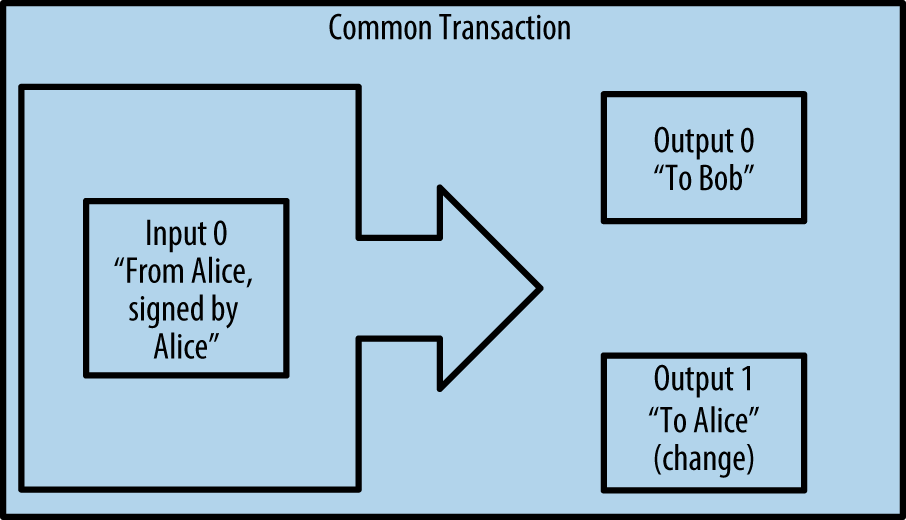
The most common form of transaction is a simple payment from one address to another, which often includes some "change" returned to the original owner. This type of transaction has one input and two outputs and is shown in [transaction-common].
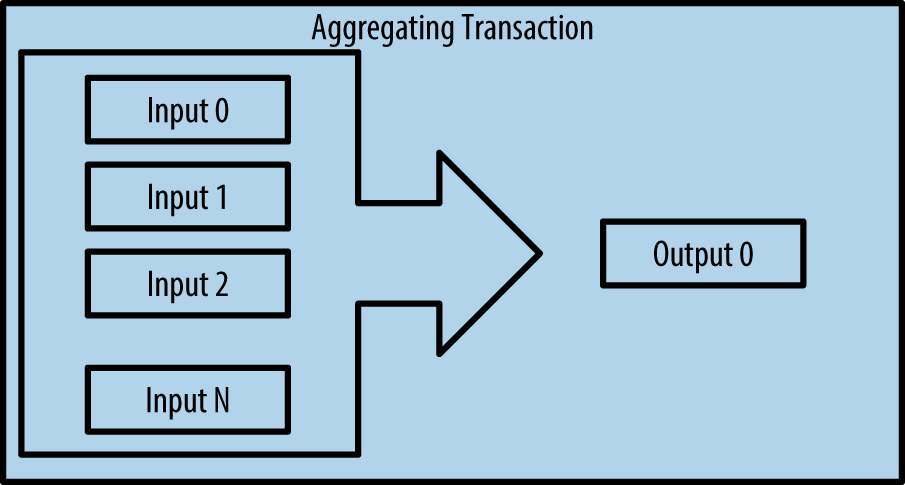
Another common form of transaction is one that aggregates several inputs into a single output (see [transaction-aggregating]). This represents the real-world equivalent of exchanging a pile of coins and currency notes for a single larger note. Transactions like these are sometimes generated by wallet applications to clean up lots of smaller amounts that were received as change for payments.
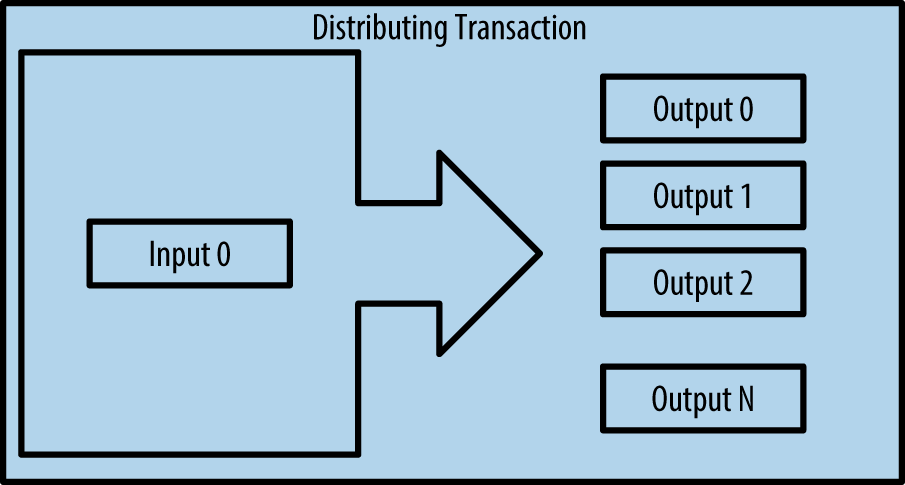
Finally, another transaction form that is seen often on the bitcoin ledger is a transaction that distributes one input to multiple outputs representing multiple recipients (see [transaction-distributing]). This type of transaction is sometimes used by commercial entities to distribute funds, such as when processing payroll payments to multiple employees.
Constructing a Transaction
Alice’s wallet application contains all the logic for selecting appropriate inputs and outputs to build a transaction to Alice’s specification. Alice only needs to specify a destination and an amount, and the rest happens in the wallet application without her seeing the details. Importantly, a wallet application can construct transactions even if it is completely offline. Like writing a check at home and later sending it to the bank in an envelope, the transaction does not need to be constructed and signed while connected to the bitcoin network.
Getting the Right Inputs
Alice’s wallet application will first have to find inputs that can pay for the amount she wants to send to Bob. Most wallets keep track of all the available outputs belonging to addresses in the wallet. Therefore, Alice’s wallet would contain a copy of the transaction output from Joe’s transaction, which was created in exchange for cash (see [getting_first_bitcoin]). A bitcoin wallet application that runs as a full-node client actually contains a copy of every unspent output from every transaction in the blockchain. This allows a wallet to construct transaction inputs as well as quickly verify incoming transactions as having correct inputs. However, because a full-node client takes up a lot of disk space, most user wallets run "lightweight" clients that track only the user’s own unspent outputs.
If the wallet application does not maintain a copy of unspent transaction outputs, it can query the bitcoin network to retrieve this information using a variety of APIs available by different providers or by asking a full-node using an application programming interface (API) call. [example_2-2] shows a API request, constructed as an HTTP GET command to a specific URL. This URL will return all the unspent transaction outputs for an address, giving any application the information it needs to construct transaction inputs for spending. We use the simple command-line HTTP client cURL to retrieve the response.
$ curl https://blockchain.info/unspent?active=1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK
{ "unspent_outputs":[ { "tx_hash":"186f9f998a5...2836dd734d2804fe65fa35779", "tx_index":104810202, "tx_output_n": 0, "script":"76a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac", "value": 10000000, "value_hex": "00989680", "confirmations":0 } ] }
The response in [example_2-2] shows one unspent output (one that has not been redeemed yet) under the ownership of Alice’s address 1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK. The response includes the reference to the transaction in which this unspent output is contained (the payment from Joe) and its value in satoshis, at 10 million, equivalent to 0.10 bitcoin. With this information, Alice’s wallet application can construct a transaction to transfer that value to new owner addresses.
|
Tip
|
View the transaction from Joe to Alice. |
As you can see, Alice’s wallet contains enough bitcoin in a single unspent output to pay for the cup of coffee. Had this not been the case, Alice’s wallet application might have to "rummage" through a pile of smaller unspent outputs, like picking coins from a purse until it could find enough to pay for the coffee. In both cases, there might be a need to get some change back, which we will see in the next section, as the wallet application creates the transaction outputs (payments).
Creating the Outputs
A transaction output is created in the form of a script that creates an encumbrance on the value and can only be redeemed by the introduction of a solution to the script. In simpler terms, Alice’s transaction output will contain a script that says something like, "This output is payable to whoever can present a signature from the key corresponding to Bob’s public address." Because only Bob has the wallet with the keys corresponding to that address, only Bob’s wallet can present such a signature to redeem this output. Alice will therefore "encumber" the output value with a demand for a signature from Bob.
This transaction will also include a second output, because Alice’s funds are in the form of a 0.10 BTC output, too much money for the 0.015 BTC cup of coffee. Alice will need 0.085 BTC in change. Alice’s change payment is created by Alice’s wallet as an output in the very same transaction as the payment to Bob. Essentially, Alice’s wallet breaks her funds into two payments: one to Bob and one back to herself. She can then use (spend) the change output in a subsequent transaction.
Finally, for the transaction to be processed by the network in a timely fashion, Alice’s wallet application will add a small fee. This is not explicit in the transaction; it is implied by the difference between inputs and outputs. If instead of taking 0.085 in change, Alice creates only 0.0845 as the second output, there will be 0.0005 BTC (half a millibitcoin) left over. The input’s 0.10 BTC is not fully spent with the two outputs, because they will add up to less than 0.10. The resulting difference is the transaction fee that is collected by the miner as a fee for validating and including the transaction in a block to be recorded on the blockchain.
The resulting transaction can be seen using a blockchain explorer web application, as shown in [transaction-alice].
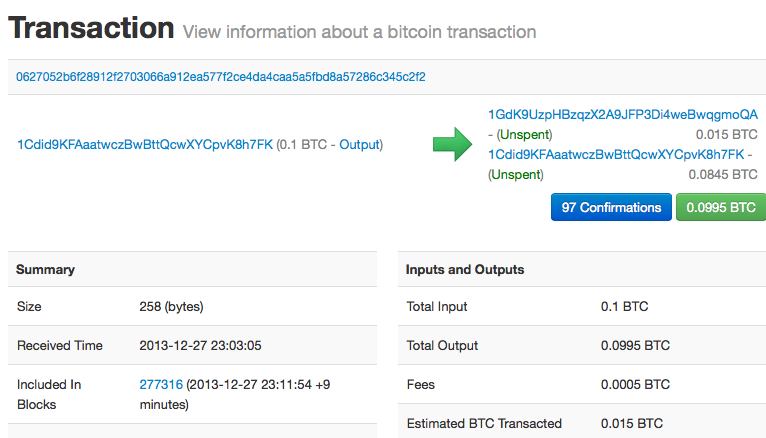
|
Tip
|
View the transaction from Alice to Bob’s Cafe. |
Adding the Transaction to the Ledger
The transaction created by Alice’s wallet application is 258 bytes long and contains everything necessary to confirm ownership of the funds and assign new owners. Now, the transaction must be transmitted to the bitcoin network where it will become part of the blockchain. In the next section we will see how a transaction becomes part of a new block and how the block is "mined." Finally, we will see how the new block, once added to the blockchain, is increasingly trusted by the network as more blocks are added.
Transmitting the transaction
Because the transaction contains all the information necessary to process, it does not matter how or where it is transmitted to the bitcoin network. The bitcoin network is a peer-to-peer network, with each bitcoin client participating by connecting to several other bitcoin clients. The purpose of the bitcoin network is to propagate transactions and blocks to all participants.
How it propagates
Any system, such as a server, desktop application, or wallet, that participates in the bitcoin network by "speaking" the bitcoin protocol is called a bitcoin node. Alice’s wallet application can send the new transaction to any bitcoin node it is connected to over any type of connection: wired, WiFi, mobile, etc. Her bitcoin wallet does not have to be connected to Bob’s bitcoin wallet directly and she does not have to use the internet connection offered by the cafe, though both those options are possible, too. Any bitcoin node that receives a valid transaction it has not seen before will immediately forward it to all other nodes to which it is connected, a propagation technique known as flooding. Thus, the transaction rapidly propagates out across the peer-to-peer network, reaching a large percentage of the nodes within a few seconds.
Bob’s view
If Bob’s bitcoin wallet application is directly connected to Alice’s wallet application, Bob’s wallet application might be the first node to receive the transaction. However, even if Alice’s wallet sends the transaction through other nodes, it will reach Bob’s wallet within a few seconds. Bob’s wallet will immediately identify Alice’s transaction as an incoming payment because it contains outputs redeemable by Bob’s keys. Bob’s wallet application can also independently verify that the transaction is well formed, uses previously unspent inputs, and contains sufficient transaction fees to be included in the next block. At this point Bob can assume, with little risk, that the transaction will shortly be included in a block and confirmed.
|
Tip
|
A common misconception about bitcoin transactions is that they must be "confirmed" by waiting 10 minutes for a new block, or up to 60 minutes for a full six confirmations. Although confirmations ensure the transaction has been accepted by the whole network, such a delay is unnecessary for small-value items such as a cup of coffee. A merchant may accept a valid small-value transaction with no confirmations, with no more risk than a credit card payment made without an ID or a signature, as merchants routinely accept today. |
Bitcoin Mining
Alice’s transaction is now propagated on the bitcoin network. It does not become part of the blockchain until it is verified and included in a block by a process called mining. See [mining] for a detailed explanation.
The bitcoin system of trust is based on computation. Transactions are bundled into blocks, which require an enormous amount of computation to prove, but only a small amount of computation to verify as proven. The mining process serves two purposes in bitcoin:
-
Mining nodes validate all transactions by reference to bitcoin’s consensus rules. Therefore, mining provides security for bitcoin transactions by rejecting invalid or malformed transactions.
-
Mining creates new bitcoin in each block, almost like a central bank printing new money. The amount of bitcoin created per block is limited and diminishes with time, following a fixed issuance schedule.
Mining achieves a fine balance between cost and reward. Mining uses electricity to solve a mathematical problem. A successful miner will collect a reward in the form of new bitcoin and transaction fees. However, the reward will only be collected if the miner has correctly validated all the transactions, to the satisfaction of the rules of consensus. This delicate balance provides security for bitcoin without a central authority.
A good way to describe mining is like a giant competitive game of sudoku that resets every time someone finds a solution and whose difficulty automatically adjusts so that it takes approximately 10 minutes to find a solution. Imagine a giant sudoku puzzle, several thousand rows and columns in size. If I show you a completed puzzle you can verify it quite quickly. However, if the puzzle has a few squares filled and the rest are empty, it takes a lot of work to solve! The difficulty of the sudoku can be adjusted by changing its size (more or fewer rows and columns), but it can still be verified quite easily even if it is very large. The "puzzle" used in bitcoin is based on a cryptographic hash and exhibits similar characteristics: it is asymmetrically hard to solve but easy to verify, and its difficulty can be adjusted.
In [user-stories], we introduced Jing, an entrepreneur in Shanghai. Jing runs a mining farm, which is a business that runs thousands of specialized mining computers, competing for the reward. Every 10 minutes or so, Jing’s mining computers compete against thousands of similar systems in a global race to find a solution to a block of transactions. Finding such a solution, the so-called Proof-of-Work (PoW), requires quadrillions of hashing operations per second across the entire bitcoin network. The algorithm for Proof-of-Work involves repeatedly hashing the header of the block and a random number with the SHA256 cryptographic algorithm until a solution matching a predetermined pattern emerges. The first miner to find such a solution wins the round of competition and publishes that block into the blockchain.
Jing started mining in 2010 using a very fast desktop computer to find a suitable Proof-of-Work for new blocks. As more miners started joining the bitcoin network, the difficulty of the problem increased rapidly. Soon, Jing and other miners upgraded to more specialized hardware, such as high-end dedicated graphical processing units (GPUs) cards such as those used in gaming desktops or consoles. At the time of this writing, the difficulty is so high that it is profitable only to mine with application-specific integrated circuits (ASIC), essentially hundreds of mining algorithms printed in hardware, running in parallel on a single silicon chip. Jing’s company also participates in a mining pool, which much like a lottery pool allows several participants to share their efforts and rewards. Jing’s company now runs a warehouse containing thousands of ASIC miners to mine for bitcoin 24 hours a day. The company pays its electricity costs by selling the bitcoin it is able to generate from mining, creating some income from the profits.
Mining Transactions in Blocks
New transactions are constantly flowing into the network from user wallets and other applications. As these are seen by the bitcoin network nodes, they get added to a temporary pool of unverified transactions maintained by each node. As miners construct a new block, they add unverified transactions from this pool to the new block and then attempt to prove the validity of that new block, with the mining algorithm (Proof-of-Work). The process of mining is explained in detail in [mining].
Transactions are added to the new block, prioritized by the highest-fee transactions first and a few other criteria. Each miner starts the process of mining a new block of transactions as soon as he receives the previous block from the network, knowing he has lost that previous round of competition. He immediately creates a new block, fills it with transactions and the fingerprint of the previous block, and starts calculating the Proof-of-Work for the new block. Each miner includes a special transaction in his block, one that pays his own bitcoin address the block reward (currently 12.5 newly created bitcoin) plus the sum of transaction fees from all the transactions included in the block. If he finds a solution that makes that block valid, he "wins" this reward because his successful block is added to the global blockchain and the reward transaction he included becomes spendable. Jing, who participates in a mining pool, has set up his software to create new blocks that assign the reward to a pool address. From there, a share of the reward is distributed to Jing and other miners in proportion to the amount of work they contributed in the last round.
Alice’s transaction was picked up by the network and included in the pool of unverified transactions. Once validated by the mining software it was included in a new block, called a candidate block, generated by Jing’s mining pool. All the miners participating in that mining pool immediately start computing Proof-of-Work for the candidate block. Approximately five minutes after the transaction was first transmitted by Alice’s wallet, one of Jing’s ASIC miners found a solution for the candidate block and announced it to the network. Once other miners validated the winning block they started the race to generate the next block.
Jing’s winning block became part of the blockchain as block #277316, containing 420 transactions, including Alice’s transaction. The block containing Alice’s transaction is counted as one "confirmation" of that transaction.
|
Tip
|
You can see the block that includes Alice’s transaction. |
Approximately 19 minutes later, a new block, #277317, is mined by another miner. Because this new block is built on top of block #277316 that contained Alice’s transaction, it added even more computation to the blockchain, thereby strengthening the trust in those transactions. Each block mined on top of the one containing the transaction counts as an additional confirmation for Alice’s transaction. As the blocks pile on top of each other, it becomes exponentially harder to reverse the transaction, thereby making it more and more trusted by the network.
In the diagram in [block-alice1], we can see block #277316, which contains Alice’s transaction. Below it are 277,316 blocks (including block #0), linked to each other in a chain of blocks (blockchain) all the way back to block #0, known as the genesis block. Over time, as the "height" in blocks increases, so does the computation difficulty for each block and the chain as a whole. The blocks mined after the one that contains Alice’s transaction act as further assurance, as they pile on more computation in a longer and longer chain. By convention, any block with more than six confirmations is considered irrevocable, because it would require an immense amount of computation to invalidate and recalculate six blocks. We will examine the process of mining and the way it builds trust in more detail in [mining].
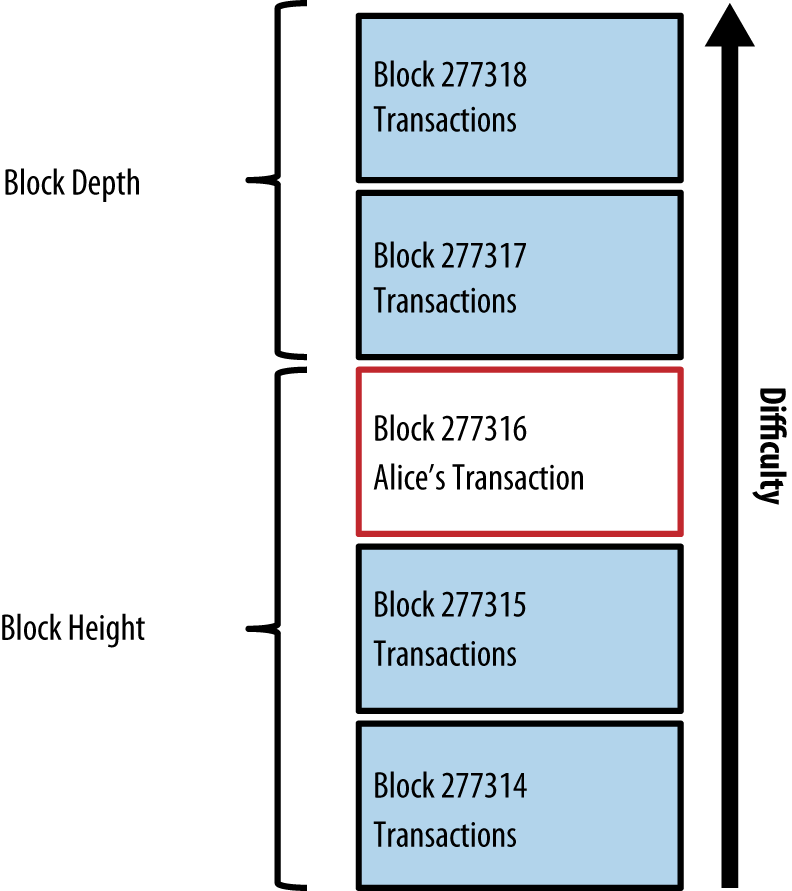
Spending the Transaction
Now that Alice’s transaction has been embedded in the blockchain as part of a block, it is part of the distributed ledger of bitcoin and visible to all bitcoin applications. Each bitcoin client can independently verify the transaction as valid and spendable. Full-node clients can track the source of the funds from the moment the bitcoin were first generated in a block, incrementally from transaction to transaction, until they reach Bob’s address. Lightweight clients can do what is called a simplified payment verification (see [spv_nodes]) by confirming that the transaction is in the blockchain and has several blocks mined after it, thus providing assurance that the miners accepted it as valid.
Bob can now spend the output from this and other transactions. For example, Bob can pay a contractor or supplier by transferring value from Alice’s coffee cup payment to these new owners. Most likely, Bob’s bitcoin software will aggregate many small payments into a larger payment, perhaps concentrating all the day’s bitcoin revenue into a single transaction. This would aggregate the various payments into a single output (and a single address). For a diagram of an aggregating transaction, see [transaction-aggregating].
As Bob spends the payments received from Alice and other customers, he extends the chain of transactions. Let’s assume that Bob pays his web designer Gopesh in Bangalore for a new website page. Now the chain of transactions will look like [block-alice2].
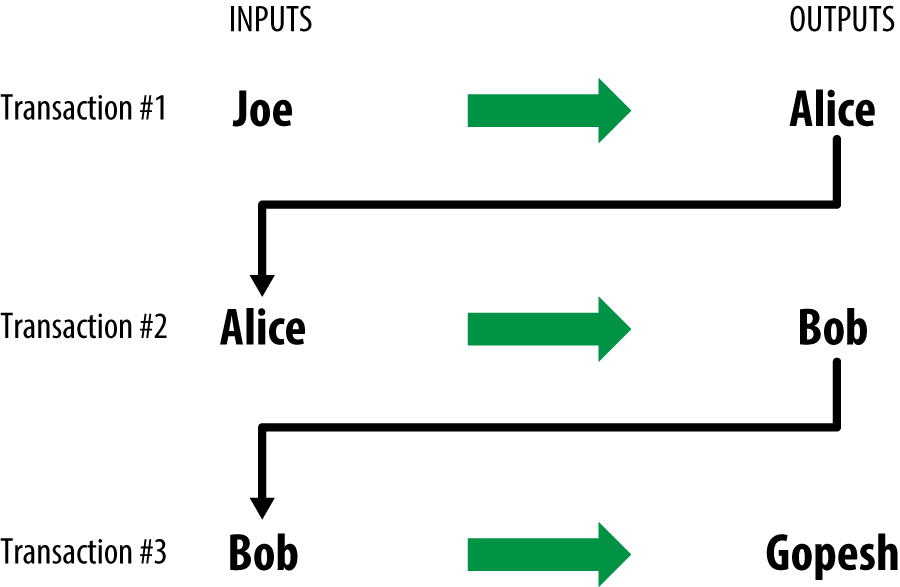
In this chapter, we saw how transactions build a chain that moves value from owner to owner. We also tracked Alice’s transaction, from the moment it was created in her wallet, through the bitcoin network and to the miners who recorded it on the blockchain. In the rest of this book we will examine the specific technologies behind wallets, addresses, signatures, transactions, the network, and finally mining.
Bitcoin Core: The Reference Implementation
Bitcoin is an open source project and the source code is available under an open (MIT) license, free to download and use for any purpose. Open source means more than simply free to use. It also means that bitcoin is developed by an open community of volunteers. At first, that community consisted of only Satoshi Nakamoto. By 2016, bitcoin’s source code had more than 400 contributors with about a dozen developers working on the code almost full-time and several dozen more on a part-time basis. Anyone can contribute to the code—including you!
When bitcoin was created by Satoshi Nakamoto, the software was actually completed before the whitepaper reproduced in [satoshi_whitepaper] was written. Satoshi wanted to make sure it worked before writing about it. That first implementation, then simply known as "Bitcoin" or "Satoshi client," has been heavily modified and improved. It has evolved into what is known as Bitcoin Core, to differentiate it from other compatible implementations. Bitcoin Core is the reference implementation of the bitcoin system, meaning that it is the authoritative reference on how each part of the technology should be implemented. Bitcoin Core implements all aspects of bitcoin, including wallets, a transaction and block validation engine, and a full network node in the peer-to-peer bitcoin network.
|
Warning
|
Even though Bitcoin Core includes a reference implementation of a wallet, this is not intended to be used as a production wallet for users or for applications. Application developers are advised to build wallets using modern standards such as BIP-39 and BIP-32 (see [mnemonic_code_words] and [hd_wallets]). BIP stands for Bitcoin Improvement Proposal. |
[bitcoin_core_architecture] shows the architecture of Bitcoin Core.
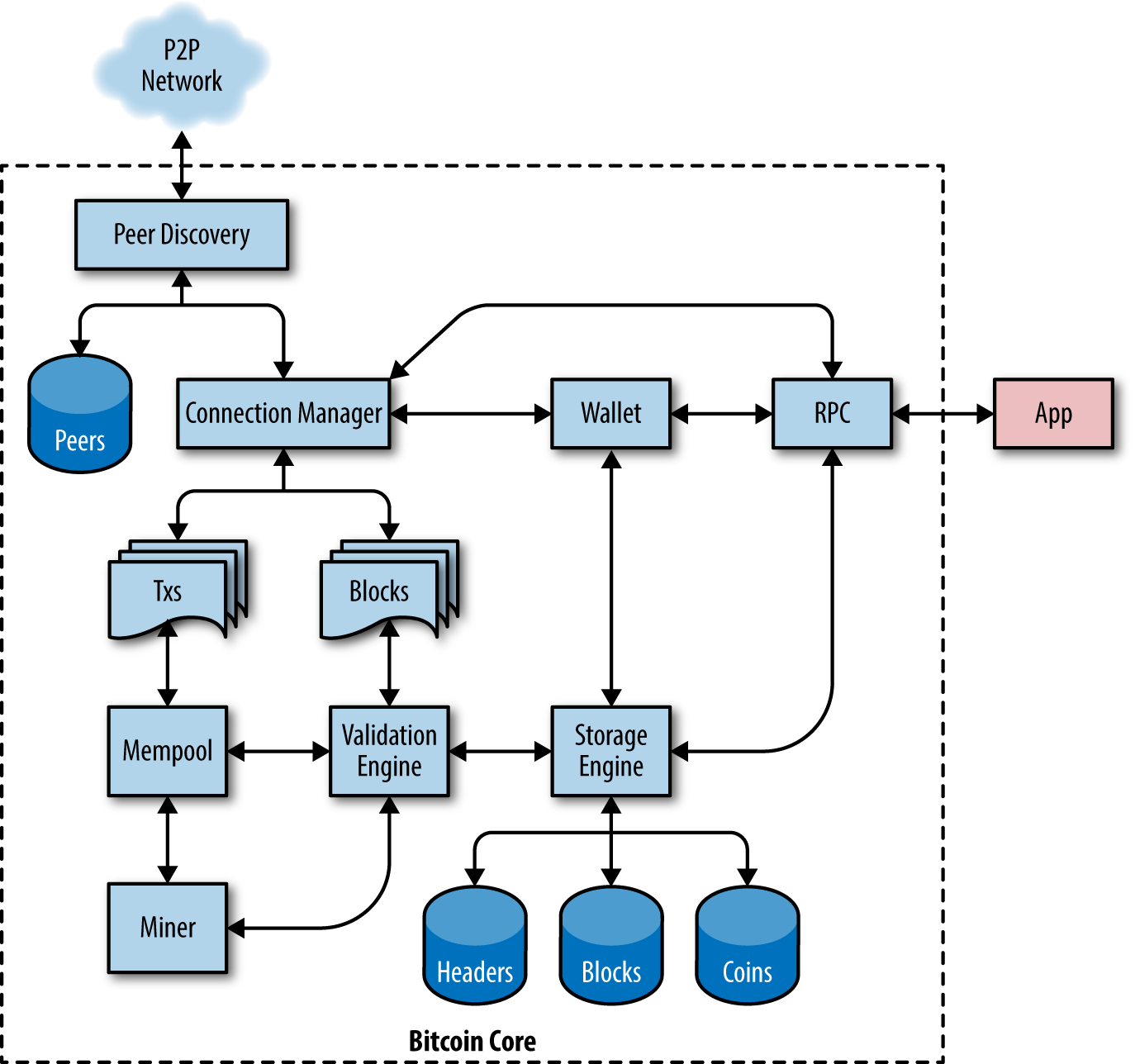
Bitcoin Development Environment
If you’re a developer, you will want to set up a development environment with all the tools, libraries, and support software for writing bitcoin applications. In this highly technical chapter, we’ll walk through that process step-by-step. If the material becomes too dense (and you’re not actually setting up a development environment) feel free to skip to the next chapter, which is less technical.
Compiling Bitcoin Core from the Source Code
Bitcoin Core’s source code can be downloaded as a ZIP archive or by cloning the authoritative source repository from GitHub. On the GitHub bitcoin page, select Download ZIP from the sidebar. Alternatively, use the git command line to create a local copy of the source code on your system.
|
Tip
|
In many of the examples in this chapter we will be using the operating system’s command-line interface (also known as a "shell"), accessed via a "terminal" application. The shell will display a prompt; you type a command; and the shell responds with some text and a new prompt for your next command. The prompt may look different on your system, but in the following examples it is denoted by a |
In this example, we are using the git command to create a local copy ("clone") of the source code:
$ git clone https://github.com/bitcoin/bitcoin.git
Cloning into 'bitcoin'...
remote: Counting objects: 66193, done.
remote: Total 66193 (delta 0), reused 0 (delta 0), pack-reused 66193
Receiving objects: 100% (66193/66193), 63.39 MiB | 574.00 KiB/s, done.
Resolving deltas: 100% (48395/48395), done.
Checking connectivity... done.
$|
Tip
|
Git is the most widely used distributed version control system, an essential part of any software developer’s toolkit. You may need to install the |
When the git cloning operation has completed, you will have a complete local copy of the source code repository in the directory bitcoin. Change to this directory by typing cd bitcoin at the prompt:
$ cd bitcoinSelecting a Bitcoin Core Release
By default, the local copy will be synchronized with the most recent code, which might be an unstable or beta version of bitcoin. Before compiling the code, select a specific version by checking out a release tag. This will synchronize the local copy with a specific snapshot of the code repository identified by a keyword tag. Tags are used by the developers to mark specific releases of the code by version number. First, to find the available tags, we use the git tag command:
$ git tag
v0.1.5
v0.1.6test1
v0.10.0
...
v0.11.2
v0.11.2rc1
v0.12.0rc1
v0.12.0rc2
...The list of tags shows all the released versions of bitcoin. By convention, release candidates, which are intended for testing, have the suffix "rc." Stable releases that can be run on production systems have no suffix. From the preceding list, select the highest version release, which at the time of writing was v0.11.2. To synchronize the local code with this version, use the git checkout command:
$ git checkout v0.11.2
HEAD is now at 7e27892... Merge pull request #6975You can confirm you have the desired version "checked out" by issuing the command git status:
$ git status
HEAD detached at v0.11.2
nothing to commit, working directory cleanConfiguring the Bitcoin Core Build
The source code includes documentation, which can be found in a number of files. Review the main documentation located in README.md in the bitcoin directory by typing more README.md at the prompt and using the spacebar to progress to the next page. In this chapter, we will build the command-line bitcoin client, also known as bitcoind on Linux. Review the instructions for compiling the bitcoind command-line client on your platform by typing more doc/build-unix.md. Alternative instructions for macOS and Windows can be found in the doc directory, as build-osx.md or build-windows.md, respectively.
Carefully review the build prerequisites, which are in the first part of the build documentation. These are libraries that must be present on your system before you can begin to compile bitcoin. If these prerequisites are missing, the build process will fail with an error. If this happens because you missed a prerequisite, you can install it and then resume the build process from where you left off. Assuming the prerequisites are installed, you start the build process by generating a set of build scripts using the autogen.sh script.
|
Note
|
The Bitcoin Core build process was changed to use the autogen/configure/make system starting with version 0.9. Older versions use a simple Makefile and work slightly differently from the following example. Follow the instructions for the version you want to compile. The autogen/configure/make introduced in 0.9 is likely to be the build system used for all future versions of the code and is the system demonstrated in the following examples. |
$ ./autogen.sh
...
glibtoolize: copying file 'build-aux/m4/libtool.m4'
glibtoolize: copying file 'build-aux/m4/ltoptions.m4'
glibtoolize: copying file 'build-aux/m4/ltsugar.m4'
glibtoolize: copying file 'build-aux/m4/ltversion.m4'
...
configure.ac:10: installing 'build-aux/compile'
configure.ac:5: installing 'build-aux/config.guess'
configure.ac:5: installing 'build-aux/config.sub'
configure.ac:9: installing 'build-aux/install-sh'
configure.ac:9: installing 'build-aux/missing'
Makefile.am: installing 'build-aux/depcomp'
...The autogen.sh script creates a set of automatic configuration scripts that will interrogate your system to discover the correct settings and ensure you have all the necessary libraries to compile the code. The most important of these is the configure script that offers a number of different options to customize the build process. Type ./configure --help to see the various options:
$ ./configure --help
`configure' configures Bitcoin Core 0.11.2 to adapt to many kinds of systems.
Usage: ./configure [OPTION]... [VAR=VALUE]...
...
Optional Features:
--disable-option-checking ignore unrecognized --enable/--with options
--disable-FEATURE do not include FEATURE (same as --enable-FEATURE=no)
--enable-FEATURE[=ARG] include FEATURE [ARG=yes]
--enable-wallet enable wallet (default is yes)
--with-gui[=no|qt4|qt5|auto]
...The configure script allows you to enable or disable certain features of bitcoind through the use of the --enable-FEATURE and --disable-FEATURE flags, where FEATURE is replaced by the feature name, as listed in the help output. In this chapter, we will build the bitcoind client with all the default features. We won’t be using the configuration flags, but you should review them to understand what optional features are part of the client. If you are in an academic setting, computer lab restrictions may require you to install applications in your home directory (e.g., using --prefix=$HOME).
Here are some useful options that override the default behavior of the configure script:
--prefix=$HOMEThis overrides the default installation location (which is /usr/local/) for the resulting executable. Use
$HOMEto put everything in your home directory, or a different path.--disable-walletThis is used to disable the reference wallet implementation.
--with-incompatible-bdbIf you are building a wallet, allow the use of an incompatible version of the Berkeley DB library.
--with-gui=noDon't build the graphical user interface, which requires the Qt library. This builds server and command-line bitcoin only.
Next, run the configure script to automatically discover all the necessary libraries and create a customized build script for your system:
$ ./configure
checking build system type... x86_64-unknown-linux-gnu
checking host system type... x86_64-unknown-linux-gnu
checking for a BSD-compatible install... /usr/bin/install -c
checking whether build environment is sane... yes
checking for a thread-safe mkdir -p... /bin/mkdir -p
checking for gawk... gawk
checking whether make sets $(MAKE)... yes
...
[many pages of configuration tests follow]
...
$If all went well, the configure command will end by creating the customized build scripts that will allow us to compile bitcoind. If there are any missing libraries or errors, the configure command will terminate with an error instead of creating the build scripts. If an error occurs, it is most likely because of a missing or incompatible library. Review the build documentation again and make sure you install the missing prerequisites. Then run configure again and see if that fixes the error.
Building the Bitcoin Core Executables
Next, you will compile the source code, a process that can take up to an hour to complete, depending on the speed of your CPU and available memory. During the compilation process you should see output every few seconds or every few minutes, or an error if something goes wrong. If an error occurs, or the compilation process is interrupted, it can be resumed any time by typing make again. Type make to start compiling the executable application:
$ make
Making all in src
CXX crypto/libbitcoinconsensus_la-hmac_sha512.lo
CXX crypto/libbitcoinconsensus_la-ripemd160.lo
CXX crypto/libbitcoinconsensus_la-sha1.lo
CXX crypto/libbitcoinconsensus_la-sha256.lo
CXX crypto/libbitcoinconsensus_la-sha512.lo
CXX libbitcoinconsensus_la-hash.lo
CXX primitives/libbitcoinconsensus_la-transaction.lo
CXX libbitcoinconsensus_la-pubkey.lo
CXX script/libbitcoinconsensus_la-bitcoinconsensus.lo
CXX script/libbitcoinconsensus_la-interpreter.lo
[... many more compilation messages follow ...]
$If all goes well, Bitcoin Core is now compiled. The final step is to install the various executables on your system using the sudo make install command. You may be prompted for your user password, because this step requires administrative privileges:
$ sudo make install
Password:
Making install in src
../build-aux/install-sh -c -d '/usr/local/lib'
libtool: install: /usr/bin/install -c bitcoind /usr/local/bin/bitcoind
libtool: install: /usr/bin/install -c bitcoin-cli /usr/local/bin/bitcoin-cli
libtool: install: /usr/bin/install -c bitcoin-tx /usr/local/bin/bitcoin-tx
...
$The default installation of bitcoind puts it in /usr/local/bin. You can confirm that Bitcoin Core is correctly installed by asking the system for the path of the executables, as follows:
$ which bitcoind
/usr/local/bin/bitcoind
$ which bitcoin-cli
/usr/local/bin/bitcoin-cliRunning a Bitcoin Core Node
Bitcoin’s peer-to-peer network is composed of network "nodes," run mostly by volunteers and some of the businesses that build bitcoin applications. Those running bitcoin nodes have a direct and authoritative view of the bitcoin blockchain, with a local copy of all the transactions, independently validated by their own system. By running a node, you don’t have to rely on any third party to validate a transaction. Moreover, by running a bitcoin node you contribute to the bitcoin network by making it more robust.
Running a node, however, requires a permanently connected system with enough resources to process all bitcoin transactions. Depending on whether you choose to index all transactions and keep a full copy of the blockchain, you may also need a lot of disk space and RAM. As of late 2016, a full-index node needs 2 GB of RAM and 125 GB of disk space so that it has room to grow. Bitcoin nodes also transmit and receive bitcoin transactions and blocks, consuming internet bandwidth. If your internet connection is limited, has a low data cap, or is metered (charged by the gigabit), you should probably not run a bitcoin node on it, or run it in a way that constrains its bandwidth (see [constrained_resources]).
|
Tip
|
Bitcoin Core keeps a full copy of the blockchain by default, with every transaction that has ever occurred on the bitcoin network since its inception in 2009. This dataset is dozens of gigabytes in size and is downloaded incrementally over several days or weeks, depending on the speed of your CPU and internet connection. Bitcoin Core will not be able to process transactions or update account balances until the full blockchain dataset is downloaded. Make sure you have enough disk space, bandwidth, and time to complete the initial synchronization. You can configure Bitcoin Core to reduce the size of the blockchain by discarding old blocks (see [constrained_resources]), but it will still download the entire dataset before discarding data. |
Despite these resource requirements, thousands of volunteers run bitcoin nodes. Some are running on systems as simple as a Raspberry Pi (a $35 USD computer the size of a pack of cards). Many volunteers also run bitcoin nodes on rented servers, usually some variant of Linux. A Virtual Private Server (VPS) or Cloud Computing Server instance can be used to run a bitcoin node. Such servers can be rented for $25 to $50 USD per month from a variety of providers.
Why would you want to run a node? Here are some of the most common reasons:
-
If you are developing bitcoin software and need to rely on a bitcoin node for programmable (API) access to the network and blockchain.
-
If you are building applications that must validate transactions according to bitcoin’s consensus rules. Typically, bitcoin software companies run several nodes.
-
If you want to support bitcoin. Running a node makes the network more robust and able to serve more wallets, more users, and more transactions.
-
If you do not want to rely on any third party to process or validate your transactions.
If you’re reading this book and interested in developing bitcoin software, you should be running your own node.
Running Bitcoin Core for the First Time
When you first run bitcoind, it will remind you to create a configuration file with a strong password for the JSON-RPC interface. This password controls access to the application programming interface (API) offered by Bitcoin Core.
Run bitcoind by typing bitcoind into the terminal:
$ bitcoind
Error: To use the "-server" option, you must set a rpcpassword in the configuration file:
/home/ubuntu/.bitcoin/bitcoin.conf
It is recommended you use the following random password:
rpcuser=bitcoinrpc
rpcpassword=2XA4DuKNCbtZXsBQRRNDEwEY2nM6M4H9Tx5dFjoAVVbK
(you do not need to remember this password)
The username and password MUST NOT be the same.
If the file does not exist, create it with owner-readable-only file permissions.
It is also recommended to set alertnotify so you are notified of problems;
for example: alertnotify=echo %s | mail -s "Bitcoin Alert" admin@foo.comAs you can see, the first time you run bitcoind it tells you that you need to build a configuration file, with at least an rpcuser and rpcpassword entry. Additionally, it is recommended that you set up the alerting mechanism. In the next section we will examine the various configuration options and set up a configuration file.
Configuring the Bitcoin Core Node
Edit the configuration file in your preferred editor and set the parameters, replacing the password with a strong password as recommended by bitcoind. Do not use the password shown in the book. Create a file inside the .bitcoin directory (under your user’s home directory) so that it is named .bitcoin/bitcoin.conf and provide a username and password:
rpcuser=bitcoinrpc rpcpassword=CHANGE_THIS
In addition to the rpcuser and rpcpassword options, Bitcoin Core offers more than 100 configuration options that modify the behavior of the network node, the storage of the blockchain, and many other aspects of its operation. To see a listing of these options, run bitcoind --help:
bitcoind --help
Bitcoin Core Daemon version v0.11.2
Usage:
bitcoind [options] Start Bitcoin Core Daemon
Options:
-?
This help message
-alerts
Receive and display P2P network alerts (default: 1)
-alertnotify=<cmd>
Execute command when a relevant alert is received or we see a really
long fork (%s in cmd is replaced by message)
...
[many more options]
...
-rpcsslciphers=<ciphers>
Acceptable ciphers (default:
TLSv1.2+HIGH:TLSv1+HIGH:!SSLv2:!aNULL:!eNULL:!3DES:@STRENGTH)Here are some of the most important options that you can set in the configuration file, or as command-line parameters to bitcoind:
- alertnotify
-
Run a specified command or script to send emergency alerts to the owner of this node, usually by email.
- conf
-
An alternative location for the configuration file. This only makes sense as a command-line parameter to
bitcoind, as it can’t be inside the configuration file it refers to. - datadir
-
Select the directory and filesystem in which to put all the blockchain data. By default this is the .bitcoin subdirectory of your home directory. Make sure this filesystem has several gigabytes of free space.
- prune
-
Reduce the disk space requirements to this many megabytes, by deleting old blocks. Use this on a resource-constrained node that can’t fit the full blockchain.
- txindex
-
Maintain an index of all transactions. This means a complete copy of the blockchain that allows you to programmatically retrieve any transaction by ID.
- maxconnections
-
Set the maximum number of nodes from which to accept connections. Reducing this from the default will reduce your bandwidth consumption. Use if you have a data cap or pay by the gigabyte.
- maxmempool
-
Limit the transaction memory pool to this many megabytes. Use it to reduce memory use of the node.
- maxreceivebuffer/maxsendbuffer
-
Limit per-connection memory buffer to this many multiples of 1000 bytes. Use on memory-constrained nodes.
- minrelaytxfee
-
Set the minimum fee transaction you will relay. Below this value, the transaction is treated as zero fee. Use this on memory-constrained nodes to reduce the size of the in-memory transaction pool.
[full_index_node] shows how you might combine the preceding options, with a fully indexed node, running as an API backend for a bitcoin application.
alertnotify=myemailscript.sh "Alert: %s"
datadir=/lotsofspace/bitcoin
txindex=1
rpcuser=bitcoinrpc
rpcpassword=CHANGE_THIS[constrained_resources] shows a resource-constrained node running on a smaller server.
alertnotify=myemailscript.sh "Alert: %s"
maxconnections=15
prune=5000
minrelaytxfee=0.0001
maxmempool=200
maxreceivebuffer=2500
maxsendbuffer=500
rpcuser=bitcoinrpc
rpcpassword=CHANGE_THISOnce you’ve edited the configuration file and set the options that best represent your needs, you can test bitcoind with this configuration. Run Bitcoin Core with the option printtoconsole to run in the foreground with output to the console:
$ bitcoind -printtoconsole
Bitcoin version v0.11.20.0
Using OpenSSL version OpenSSL 1.0.2e 3 Dec 2015
Startup time: 2015-01-02 19:56:17
Using data directory /tmp/bitcoin
Using config file /tmp/bitcoin/bitcoin.conf
Using at most 125 connections (275 file descriptors available)
Using 2 threads for script verification
scheduler thread start
HTTP: creating work queue of depth 16
No rpcpassword set - using random cookie authentication
Generated RPC authentication cookie /tmp/bitcoin/.cookie
HTTP: starting 4 worker threads
Bound to [::]:8333
Bound to 0.0.0.0:8333
Cache configuration:
* Using 2.0MiB for block index database
* Using 32.5MiB for chain state database
* Using 65.5MiB for in-memory UTXO set
init message: Loading block index...
Opening LevelDB in /tmp/bitcoin/blocks/index
Opened LevelDB successfully
[... more startup messages ...]You can hit Ctrl-C to interrupt the process once you are satisfied that it is loading the correct settings and running as you expect.
To run Bitcoin Core in the background as a process, start it with the daemon option, as bitcoind -daemon.
To monitor the progress and runtime status of your bitcoin node, use the command bitcoin-cli getinfo:
$ bitcoin-cli getinfo{ "version" : 110200, "protocolversion" : 70002, "blocks" : 396328, "timeoffset" : 0, "connections" : 15, "proxy" : "", "difficulty" : 120033340651.23696899, "testnet" : false, "relayfee" : 0.00010000, "errors" : "" }
This shows a node running Bitcoin Core version 0.11.2, with a blockchain height of 396328 blocks and 15 active network connections.
Once you are happy with the configuration options you have selected, you should add bitcoin to the startup scripts in your operating system, so that it runs continuously and restarts when the operating system restarts. You will find a number of example startup scripts for various operating systems in bitcoin’s source directory under contrib/init and a README.md file showing which system uses which script.
Bitcoin Core Application Programming Interface (API)
The Bitcoin Core client implements a JSON-RPC interface that can also be accessed using the command-line helper bitcoin-cli. The command line allows us to experiment interactively with the capabilities that are also available programmatically via the API. To start, invoke the help command to see a list of the available bitcoin RPC commands:
$ bitcoin-cli help
addmultisigaddress nrequired ["key",...] ( "account" )
addnode "node" "add|remove|onetry"
backupwallet "destination"
createmultisig nrequired ["key",...]
createrawtransaction [{"txid":"id","vout":n},...] {"address":amount,...}
decoderawtransaction "hexstring"
...
...
verifymessage "bitcoinaddress" "signature" "message"
walletlock
walletpassphrase "passphrase" timeout
walletpassphrasechange "oldpassphrase" "newpassphrase"Each of these commands may take a number of parameters. To get additional help, a detailed description, and information on the parameters, add the command name after help. For example, to see help on the getblockhash RPC command:
$ bitcoin-cli help getblockhash
getblockhash index
Returns hash of block in best-block-chain at index provided.
Arguments:
1. index (numeric, required) The block index
Result:
"hash" (string) The block hash
Examples:
> bitcoin-cli getblockhash 1000
> curl --user myusername --data-binary '{"jsonrpc": "1.0", "id":"curltest", "method": "getblockhash", "params": [1000] }' -H 'content-type: text/plain;' http://127.0.0.1:8332/At the end of the help information you will see two examples of the RPC command, using the bitcoin-cli helper or the HTTP client curl. These examples demonstrate how you might call the command. Copy the first example and see the result:
$ bitcoin-cli getblockhash 1000
00000000c937983704a73af28acdec37b049d214adbda81d7e2a3dd146f6ed09The result is a block hash, which is described in more detail in the following chapters. But for now, this command should return the same result on your system, demonstrating that your Bitcoin Core node is running, is accepting commands, and has information about block 1000 to return to you.
In the next sections we will demonstrate some very useful RPC commands and their expected output.
Getting Information on the Bitcoin Core Client Status
Command: getinfo
Bitcoin’s getinfo RPC command displays basic information about the status of the bitcoin network node, the wallet, and the blockchain database. Use bitcoin-cli to run it:
$ bitcoin-cli getinfo{ "version" : 110200, "protocolversion" : 70002, "blocks" : 396367, "timeoffset" : 0, "connections" : 15, "proxy" : "", "difficulty" : 120033340651.23696899, "testnet" : false, "relayfee" : 0.00010000, "errors" : "" }
The data is returned in JavaScript Object Notation (JSON), a format that can easily be "consumed" by all programming languages but is also quite human-readable. Among this data we see the version numbers for the bitcoin software client (110200) and bitcoin protocol (70002). We see the current block height, showing us how many blocks are known to this client (396367). We also see various statistics about the bitcoin network and the settings related to this client.
|
Tip
|
It will take some time, perhaps more than a day, for the |
Exploring and Decoding Transactions
Commands: getrawtransaction, decoderawtransaction
In [cup_of_coffee], Alice bought a cup of coffee from Bob’s Cafe. Her transaction was recorded on the blockchain with transaction ID (txid) 0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2. Let’s use the API to retrieve and examine that transaction by passing the transaction ID as a parameter:
$ bitcoin-cli getrawtransaction 0627052b6f28912f2703066a912ea577f2ce4da4caa5a↵ 5fbd8a57286c345c2f2 0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd734d2804fe65fa35779000↵ 000008b483045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4↵ ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813014↵ 10484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc54123363767↵ 89d172787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adfffffffff0260e3160000000↵ 0001976a914ab68025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef8000000000001976a9↵ 147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac00000000
|
Tip
|
A transaction ID is not authoritative until a transaction has been confirmed. Absence of a transaction hash in the blockchain does not mean the transaction was not processed. This is known as "transaction malleability," because transaction hashes can be modified prior to confirmation in a block. After confirmation, the txid is immutable and authoritative. |
The command getrawtransaction returns a serialized transaction in hexadecimal notation. To decode that, we use the decoderawtransaction command, passing the hex data as a parameter. You can copy the hex returned by getrawtransaction and paste it as a parameter to decoderawtransaction:
$ bitcoin-cli decoderawtransaction 0100000001186f9f998a5aa6f048e51dd8419a14d8↵ a0f1a8a2836dd734d2804fe65fa35779000000008b483045022100884d142d86652a3f47ba474↵ 6ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298↵ cad530a863ea8f53982c09db8f6e381301410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fd↵ e0735e7ade8416ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc17b4a10fa↵ 336a8d752adfffffffff0260e31600000000001976a914ab68025513c3dbd2f7b92a94e0581f5↵ d50f654e788acd0ef8000000000001976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8↵ 88ac00000000
{
"txid": "0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"size": 258,
"version": 1,
"locktime": 0,
"vin": [
{
"txid": "7957a35fe64f80d234d76d83a2...8149a41d81de548f0a65a8a999f6f18",
"vout": 0,
"scriptSig": {
"asm":"3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1decc...",
"hex":"483045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1de..."
},
"sequence": 4294967295
}
],
"vout": [
{
"value": 0.01500000,
"n": 0,
"scriptPubKey": {
"asm": "OP_DUP OP_HASH160 ab68...5f654e7 OP_EQUALVERIFY OP_CHECKSIG",
"hex": "76a914ab68025513c3dbd2f7b92a94e0581f5d50f654e788ac",
"reqSigs": 1,
"type": "pubkeyhash",
"addresses": [
"1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA"
]
}
},
{
"value": 0.08450000,
"n": 1,
"scriptPubKey": {
"asm": "OP_DUP OP_HASH160 7f9b1a...025a8 OP_EQUALVERIFY OP_CHECKSIG",
"hex": "76a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac",
"reqSigs": 1,
"type": "pubkeyhash",
"addresses": [
"1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK"
]
}
}
]
}
The transaction decode shows all the components of this transaction, including the transaction inputs and outputs. In this case we see that the transaction that credited our new address with 50 millibits used one input and generated two outputs. The input to this transaction was the output from a previously confirmed transaction (shown as the vin txid starting with 7957a35fe). The two outputs correspond to the 50 millibit credit and an output with change back to the sender.
We can further explore the blockchain by examining the previous transaction referenced by its txid in this transaction using the same commands (e.g., getrawtransaction). Jumping from transaction to transaction we can follow a chain of transactions back as the coins are transmitted from owner address to owner address.
Exploring Blocks
Commands: getblock, getblockhash
Exploring blocks is similar to exploring transactions. However, blocks can be referenced either by the block height or by the block hash. First, let’s find a block by its height. In [cup_of_coffee], we saw that Alice’s transaction was included in block 277316.
We use the getblockhash command, which takes the block height as the parameter and returns the block hash for that block:
$ bitcoin-cli getblockhash 277316 0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4
Now that we know which block Alice’s transaction was included in, we can query that block. We use the getblock command with the block hash as the parameter:
$ bitcoin-cli getblock 0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b3↵ 1b2cc7bdc4
{
"hash": "0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4",
"confirmations": 37371,
"size": 218629,
"height": 277316,
"version": 2,
"merkleroot": "c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2e",
"tx": [
"d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f",
"b268b45c59b39d759614757718b9918caf0ba9d97c56f3b91956ff877c503fbe",
"04905ff987ddd4cfe603b03cfb7ca50ee81d89d1f8f5f265c38f763eea4a21fd",
"32467aab5d04f51940075055c2f20bbd1195727c961431bf0aff8443f9710f81",
"561c5216944e21fa29dd12aaa1a45e3397f9c0d888359cb05e1f79fe73da37bd",
[... hundreds of transactions ...]
"78b300b2a1d2d9449b58db7bc71c3884d6e0579617e0da4991b9734cef7ab23a",
"6c87130ec283ab4c2c493b190c20de4b28ff3caf72d16ffa1ce3e96f2069aca9",
"6f423dbc3636ef193fd8898dfdf7621dcade1bbe509e963ffbff91f696d81a62",
"802ba8b2adabc5796a9471f25b02ae6aeee2439c679a5c33c4bbcee97e081196",
"eaaf6a048588d9ad4d1c092539bd571dd8af30635c152a3b0e8b611e67d1a1af",
"e67abc6bd5e2cac169821afc51b207127f42b92a841e976f9b752157879ba8bd",
"d38985a6a1bfd35037cb7776b2dc86797abbb7a06630f5d03df2785d50d5a2ac",
"45ea0a3f6016d2bb90ab92c34a7aac9767671a8a84b9bcce6c019e60197c134b",
"c098445d748ced5f178ef2ff96f2758cbec9eb32cb0fc65db313bcac1d3bc98f"
],
"time": 1388185914,
"mediantime": 1388183675,
"nonce": 924591752,
"bits": "1903a30c",
"difficulty": 1180923195.258026,
"chainwork": "000000000000000000000000000000000000000000000934695e92aaf53afa1a",
"previousblockhash": "0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569",
"nextblockhash": "000000000000000010236c269dd6ed714dd5db39d36b33959079d78dfd431ba7"
}
The block contains 419 transactions and the 64th transaction listed (0627052b…) is Alice’s coffee payment. The height entry tells us this is the 277316th block in the blockchain.
Using Bitcoin Core’s Programmatic Interface
The bitcoin-cli helper is very useful for exploring the Bitcoin Core API and testing functions. But the whole point of an application programming interface is to access functions programmatically. In this section we will demonstrate accessing Bitcoin Core from another program.
Bitcoin Core’s API is a JSON-RPC interface. JSON stands for JavaScript Object Notation and it is a very convenient way to present data that both humans and programs can easily read. RPC stands for Remote Procedure Call, which means that we are calling procedures (functions) that are remote (on the Bitcoin Core node) via a network protocol. In this case, the network protocol is HTTP, or HTTPS (for encrypted connections).
When we used the bitcoin-cli command to get help on a command, it showed us an example of using curl, the versatile command-line HTTP client to construct one of these JSON-RPC calls:
$ curl --user myusername --data-binary '{"jsonrpc": "1.0", "id":"curltest", "method": "getinfo", "params": [] }' -H 'content-type: text/plain;' http://127.0.0.1:8332/This command shows that curl submits an HTTP request to the local host (127.0.0.1), connecting to the default bitcoin port (8332), and submitting a jsonrpc request for the getinfo method using text/plain encoding.
If you’re implementing a JSON-RPC call in your own program, you can use a generic HTTP library to construct the call, similar to what is shown in the preceding curl example.
However, there are libraries in most every programming language that "wrap" the Bitcoin Core API in a way that makes this a lot simpler. We will use the python-bitcoinlib library to simplify API access. Remember, this requires you to have a running Bitcoin Core instance, which will be used to make JSON-RPC calls.
The Python script in [rpc_example] makes a simple getinfo call and prints the block parameter from the data returned by Bitcoin Core.
from bitcoin.rpc import RawProxy # Create a connection to local Bitcoin Core node p = RawProxy() # Run the getinfo command, store the resulting data in info info = p.getinfo() # Retrieve the 'blocks' element from the info print(info['blocks'])
Running it gives us the following result:
$ python rpc_example.py
394075It tells us that our local Bitcoin Core node has 394075 blocks in its blockchain. Not a spectacular result, but it demonstrates the basic use of the library as a simplified interface to Bitcoin Core’s JSON-RPC API.
Next, let’s use the getrawtransaction and decodetransaction calls to retrieve the details of Alice’s coffee payment. In [rpc_transaction], we retrieve Alice’s transaction and list the transaction’s outputs. For each output, we show the recipient address and value. As a reminder, Alice’s transaction had one output paying Bob’s Cafe and one output for change back to Alice.
from bitcoin.rpc import RawProxy p = RawProxy() # Alice's transaction ID txid = "0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2" # First, retrieve the raw transaction in hex raw_tx = p.getrawtransaction(txid) # Decode the transaction hex into a JSON object decoded_tx = p.decoderawtransaction(raw_tx) # Retrieve each of the outputs from the transaction for output in decoded_tx['vout']: print(output['scriptPubKey']['addresses'], output['value'])
Running this code, we get:
$ python rpc_transaction.py
([u'1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA'], Decimal('0.01500000'))
([u'1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK'], Decimal('0.08450000'))Both of the preceding examples are rather simple. You don’t really need a program to run them; you could just as easily use the bitcoin-cli helper. The next example, however, requires several hundred RPC calls and more clearly demonstrates the use of a programmatic interface.
In [rpc_block], we first retrieve block 277316, then retrieve each of the 419 transactions within by reference to each transaction ID. Next, we iterate through each of the transaction’s outputs and add up the value.
from bitcoin.rpc import RawProxy p = RawProxy() # The block height where Alice's transaction was recorded blockheight = 277316 # Get the block hash of block with height 277316 blockhash = p.getblockhash(blockheight) # Retrieve the block by its hash block = p.getblock(blockhash) # Element tx contains the list of all transaction IDs in the block transactions = block['tx'] block_value = 0 # Iterate through each transaction ID in the block for txid in transactions: tx_value = 0 # Retrieve the raw transaction by ID raw_tx = p.getrawtransaction(txid) # Decode the transaction decoded_tx = p.decoderawtransaction(raw_tx) # Iterate through each output in the transaction for output in decoded_tx['vout']: # Add up the value of each output tx_value = tx_value + output['value'] # Add the value of this transaction to the total block_value = block_value + tx_value print("Total value in block: ", block_value)
Running this code, we get:
$ python rpc_block.py
('Total value in block: ', Decimal('10322.07722534'))Our example code calculates that the total value transacted in this block is 10,322.07722534 BTC (including 25 BTC reward and 0.0909 BTC in fees). Compare that to the amount reported by a block explorer site by searching for the block hash or height. Some block explorers report the total value excluding the reward and excluding the fees. See if you can spot the difference.
Alternative Clients, Libraries, and Toolkits
There are many alternative clients, libraries, toolkits, and even full-node implementations in the bitcoin ecosystem. These are implemented in a variety of programming languages, offering programmers native interfaces in their preferred language.
The following sections list some of the best libraries, clients, and toolkits, organized by programming languages.
C/C++
- Bitcoin Core
-
The reference implementation of bitcoin
- libbitcoin
-
Cross-platform C++ development toolkit, node, and consensus library
- bitcoin explorer
-
Libbitcoin’s command-line tool
- picocoin
-
A C language lightweight client library for bitcoin by Jeff Garzik
JavaScript
Java
- bitcoinj
-
A Java full-node client library
- Bits of Proof (BOP)
-
A Java enterprise-class implementation of bitcoin
Python
- python-bitcoinlib
-
A Python bitcoin library, consensus library, and node by Peter Todd
- pycoin
-
A Python bitcoin library by Richard Kiss
- pybitcointools
-
A Python bitcoin library by Vitalik Buterin
Ruby
- bitcoin-client
-
A Ruby library wrapper for the JSON-RPC API
Go
- btcd
-
A Go language full-node bitcoin client
Rust
- rust-bitcoin
-
Rust bitcoin library for serialization, parsing, and API calls
C#
- NBitcoin
-
Comprehensive bitcoin library for the .NET framework
Objective-C
- CoreBitcoin
-
Bitcoin toolkit for ObjC and Swift
Many more libraries exist in a variety of other programming languages and more are created all the time.
Keys, Addresses
You may have heard that bitcoin is based on cryptography, which is a branch of mathematics used extensively in computer security. Cryptography means "secret writing" in Greek, but the science of cryptography encompasses more than just secret writing, which is referred to as encryption. Cryptography can also be used to prove knowledge of a secret without revealing that secret (digital signature), or prove the authenticity of data (digital fingerprint). These types of cryptographic proofs are the mathematical tools critical to bitcoin and used extensively in bitcoin applications. Ironically, encryption is not an important part of bitcoin, as its communications and transaction data are not encrypted and do not need to be encrypted to protect the funds. In this chapter we will introduce some of the cryptography used in bitcoin to control ownership of funds, in the form of keys, addresses, and wallets.
Introduction
Ownership of bitcoin is established through digital keys, bitcoin addresses, and digital signatures. The digital keys are not actually stored in the network, but are instead created and stored by users in a file, or simple database, called a wallet. The digital keys in a user’s wallet are completely independent of the bitcoin protocol and can be generated and managed by the user’s wallet software without reference to the blockchain or access to the internet. Keys enable many of the interesting properties of bitcoin, including decentralized trust and control, ownership attestation, and the cryptographic-proof security model.
Most bitcoin transactions requires a valid digital signature to be included in the blockchain, which can only be generated with a secret key; therefore, anyone with a copy of that key has control of the bitcoin. The digital signature used to spend funds is also referred to as a witness, a term used in cryptography. The witness data in a bitcoin transaction testifies to the true ownership of the funds being spent.
Keys come in pairs consisting of a private (secret) key and a public key. Think of the public key as similar to a bank account number and the private key as similar to the secret PIN, or signature on a check, that provides control over the account. These digital keys are very rarely seen by the users of bitcoin. For the most part, they are stored inside the wallet file and managed by the bitcoin wallet software.
In the payment portion of a bitcoin transaction, the recipient’s public key is represented by its digital fingerprint, called a bitcoin address, which is used in the same way as the beneficiary name on a check (i.e., "Pay to the order of"). In most cases, a bitcoin address is generated from and corresponds to a public key. However, not all bitcoin addresses represent public keys; they can also represent other beneficiaries such as scripts, as we will see later in this chapter. This way, bitcoin addresses abstract the recipient of funds, making transaction destinations flexible, similar to paper checks: a single payment instrument that can be used to pay into people’s accounts, pay into company accounts, pay for bills, or pay to cash. The bitcoin address is the only representation of the keys that users will routinely see, because this is the part they need to share with the world.
First, we will introduce cryptography and explain the mathematics used in bitcoin. Next, we will look at how keys are generated, stored, and managed. We will review the various encoding formats used to represent private and public keys, addresses, and script addresses. Finally, we will look at advanced use of keys and addresses: vanity, multisignature, and script addresses and paper wallets.
Public Key Cryptography and Cryptocurrency
Public key cryptography was invented in the 1970s and is a mathematical foundation for computer and information security.
Since the invention of public key cryptography, several suitable mathematical functions, such as prime number exponentiation and elliptic curve multiplication, have been discovered. These mathematical functions are practically irreversible, meaning that they are easy to calculate in one direction and infeasible to calculate in the opposite direction. Based on these mathematical functions, cryptography enables the creation of digital secrets and unforgeable digital signatures. Bitcoin uses elliptic curve multiplication as the basis for its cryptography.
In bitcoin, we use public key cryptography to create a key pair that controls access to bitcoin. The key pair consists of a private key and—derived from it—a unique public key. The public key is used to receive funds, and the private key is used to sign transactions to spend the funds.
There is a mathematical relationship between the public and the private key that allows the private key to be used to generate signatures on messages. This signature can be validated against the public key without revealing the private key.
When spending bitcoin, the current bitcoin owner presents her public key and a signature (different each time, but created from the same private key) in a transaction to spend those bitcoin. Through the presentation of the public key and signature, everyone in the bitcoin network can verify and accept the transaction as valid, confirming that the person transferring the bitcoin owned them at the time of the transfer.
|
Tip
|
In most wallet implementations, the private and public keys are stored together as a key pair for convenience. However, the public key can be calculated from the private key, so storing only the private key is also possible. |
Private and Public Keys
A bitcoin wallet contains a collection of key pairs, each consisting of a private key and a public key. The private key (k) is a number, usually picked at random. From the private key, we use elliptic curve multiplication, a one-way cryptographic function, to generate a public key (K). From the public key (K), we use a one-way cryptographic hash function to generate a bitcoin address (A). In this section, we will start with generating the private key, look at the elliptic curve math that is used to turn that into a public key, and finally, generate a bitcoin address from the public key. The relationship between private key, public key, and bitcoin address is shown in [k_to_K_to_A].
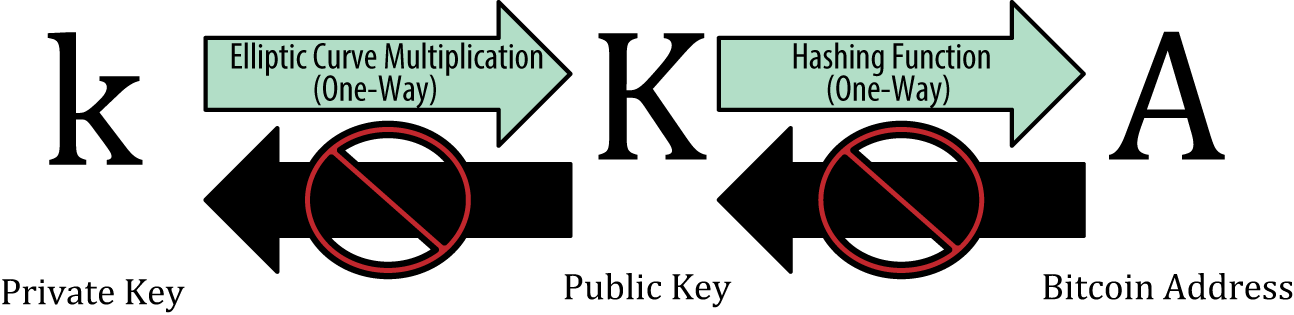
Private Keys
A private key is simply a number, picked at random. Ownership and control over the private key is the root of user control over all funds associated with the corresponding bitcoin address. The private key is used to create signatures that are required to spend bitcoin by proving ownership of funds used in a transaction. The private key must remain secret at all times, because revealing it to third parties is equivalent to giving them control over the bitcoin secured by that key. The private key must also be backed up and protected from accidental loss, because if it’s lost it cannot be recovered and the funds secured by it are forever lost, too.
|
Tip
|
The bitcoin private key is just a number. You can pick your private keys randomly using just a coin, pencil, and paper: toss a coin 256 times and you have the binary digits of a random private key you can use in a bitcoin wallet. The public key can then be generated from the private key. |
Generating a private key from a random number
The first and most important step in generating keys is to find a secure source of entropy, or randomness. Creating a bitcoin key is essentially the same as "Pick a number between 1 and 2256." The exact method you use to pick that number does not matter as long as it is not predictable or repeatable. Bitcoin software uses the underlying operating system’s random number generators to produce 256 bits of entropy (randomness). Usually, the OS random number generator is initialized by a human source of randomness, which is why you may be asked to wiggle your mouse around for a few seconds.
More precisely, the private key can be any number between 1 and n - 1, where n is a constant (n = 1.158 * 1077, slightly less than 2256) defined as the order of the elliptic curve used in bitcoin (see [elliptic_curve]). To create such a key, we randomly pick a 256-bit number and check that it is less than n - 1. In programming terms, this is usually achieved by feeding a larger string of random bits, collected from a cryptographically secure source of randomness, into the SHA256 hash algorithm, which will conveniently produce a 256-bit number. If the result is less than n - 1, we have a suitable private key. Otherwise, we simply try again with another random number.
|
Warning
|
Do not write your own code to create a random number or use a "simple" random number generator offered by your programming language. Use a cryptographically secure pseudorandom number generator (CSPRNG) with a seed from a source of sufficient entropy. Study the documentation of the random number generator library you choose to make sure it is cryptographically secure. Correct implementation of the CSPRNG is critical to the security of the keys. |
The following is a randomly generated private key (k) shown in hexadecimal format (256 bits shown as 64 hexadecimal digits, each 4 bits):
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD|
Tip
|
The size of bitcoin’s private key space, (2256) is an unfathomably large number. It is approximately 1077 in decimal. For comparison, the visible universe is estimated to contain 1080 atoms. |
To generate a new key with the Bitcoin Core client (see [ch03_bitcoin_client]), use the getnewaddress command. For security reasons it displays the public key only, not the private key. To ask bitcoind to expose the private key, use the dumpprivkey command. The dumpprivkey command shows the private key in a Base58 checksum-encoded format called the Wallet Import Format (WIF), which we will examine in more detail in [priv_formats]. Here’s an example of generating and displaying a private key using these two commands:
$ bitcoin-cli getnewaddress
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
$ bitcoin-cli dumpprivkey 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJThe dumpprivkey command opens the wallet and extracts the private key that was generated by the getnewaddress command. It is not possible for bitcoind to know the private key from the public key unless they are both stored in the wallet.
|
Tip
|
The |
You can also use the Bitcoin Explorer command-line tool (see [appdx_bx]) to generate and display private keys with the commands seed, ec-new, and ec-to-wif:
$ bx seed | bx ec-new | bx ec-to-wif
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1JcnPublic Keys
The public key is calculated from the private key using elliptic curve multiplication, which is irreversible: K = k * G, where k is the private key, G is a constant point called the generator point, and K is the resulting public key. The reverse operation, known as "finding the discrete logarithm"—calculating k if you know K—is as difficult as trying all possible values of k, i.e., a brute-force search. Before we demonstrate how to generate a public key from a private key, let’s look at elliptic curve cryptography in a bit more detail.
|
Tip
|
Elliptic curve multiplication is a type of function that cryptographers call a "trap door" function: it is easy to do in one direction (multiplication) and impossible to do in the reverse direction (division). The owner of the private key can easily create the public key and then share it with the world knowing that no one can reverse the function and calculate the private key from the public key. This mathematical trick becomes the basis for unforgeable and secure digital signatures that prove ownership of bitcoin funds. |
Elliptic Curve Cryptography Explained
Elliptic curve cryptography is a type of asymmetric or public key cryptography based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve.
[ecc-curve] is an example of an elliptic curve, similar to that used by bitcoin.
Bitcoin uses a specific elliptic curve and set of mathematical constants, as defined in a standard called secp256k1, established by the National Institute of Standards and Technology (NIST). The secp256k1 curve is defined by the following function, which produces an elliptic curve:
or
The mod p (modulo prime number p) indicates that this curve is over a finite field of prime order p, also written as \( \mathbb{F}_p \), where p = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1, a very large prime number.
Because this curve is defined over a finite field of prime order instead of over the real numbers, it looks like a pattern of dots scattered in two dimensions, which makes it difficult to visualize. However, the math is identical to that of an elliptic curve over real numbers. As an example, [ecc-over-F17-math] shows the same elliptic curve over a much smaller finite field of prime order 17, showing a pattern of dots on a grid. The secp256k1 bitcoin elliptic curve can be thought of as a much more complex pattern of dots on a unfathomably large grid.
So, for example, the following is a point P with coordinates (x,y) that is a point on the secp256k1 curve:
P = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424)[example_4_1] shows how you can check this yourself using Python:
In elliptic curve math, there is a point called the "point at infinity," which roughly corresponds to the role of zero in addition. On computers, it’s sometimes represented by x = y = 0 (which doesn’t satisfy the elliptic curve equation, but it’s an easy separate case that can be checked).
There is also a + operator, called "addition," which has some properties similar to the traditional addition of real numbers that gradeschool children learn. Given two points P1 and P2 on the elliptic curve, there is a third point P3 = P1 + P2, also on the elliptic curve.
Geometrically, this third point P3 is calculated by drawing a line between P1 and P2. This line will intersect the elliptic curve in exactly one additional place. Call this point P3' = (x, y). Then reflect in the x-axis to get P3 = (x, –y).
There are a couple of special cases that explain the need for the "point at infinity."
If P1 and P2 are the same point, the line "between" P1 and P2 should extend to be the tangent on the curve at this point P1. This tangent will intersect the curve in exactly one new point. You can use techniques from calculus to determine the slope of the tangent line. These techniques curiously work, even though we are restricting our interest to points on the curve with two integer coordinates!
In some cases (i.e., if P1 and P2 have the same x values but different y values), the tangent line will be exactly vertical, in which case P3 = "point at infinity."
If P1 is the "point at infinity," then P1 + P2 = P2. Similarly, if P2 is the point at infinity, then P1 + P2 = P1. This shows how the point at infinity plays the role of zero.
It turns out that + is associative, which means that (A + B) + C = A + (B + C). That means we can write A + B + C without parentheses and without ambiguity.
Now that we have defined addition, we can define multiplication in the standard way that extends addition. For a point P on the elliptic curve, if k is a whole number, then kP = P + P + P + … + P (k times). Note that k is sometimes confusingly called an "exponent" in this case.
Generating a Public Key
Starting with a private key in the form of a randomly generated number k, we multiply it by a predetermined point on the curve called the generator point G to produce another point somewhere else on the curve, which is the corresponding public key K. The generator point is specified as part of the secp256k1 standard and is always the same for all keys in bitcoin:
where k is the private key, G is the generator point, and K is the resulting public key, a point on the curve. Because the generator point is always the same for all bitcoin users, a private key k multiplied with G will always result in the same public key K. The relationship between k and K is fixed, but can only be calculated in one direction, from k to K. That’s why a bitcoin address (derived from K) can be shared with anyone and does not reveal the user’s private key (k).
|
Tip
|
A private key can be converted into a public key, but a public key cannot be converted back into a private key because the math only works one way. |
Implementing the elliptic curve multiplication, we take the private key k generated previously and multiply it with the generator point G to find the public key K:
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * GPublic key K is defined as a point K = (x,y):
K = (x, y)
where,
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDBTo visualize multiplication of a point with an integer, we will use the simpler elliptic curve over real numbers—remember, the math is the same. Our goal is to find the multiple kG of the generator point G, which is the same as adding G to itself, k times in a row. In elliptic curves, adding a point to itself is the equivalent of drawing a tangent line on the point and finding where it intersects the curve again, then reflecting that point on the x-axis.
[ecc_illustrated] shows the process for deriving G, 2G, 4G, as a geometric operation on the curve.
|
Tip
|
Most bitcoin implementations use the OpenSSL cryptographic library to do the elliptic curve math. For example, to derive the public key, the function |
Bitcoin Addresses
A bitcoin address is a string of digits and characters that can be shared with anyone who wants to send you money. Addresses produced from public keys consist of a string of numbers and letters, beginning with the digit "1." Here’s an example of a bitcoin address:
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZyThe bitcoin address is what appears most commonly in a transaction as the "recipient" of the funds. If we compare a bitcoin transaction to a paper check, the bitcoin address is the beneficiary, which is what we write on the line after "Pay to the order of." On a paper check, that beneficiary can sometimes be the name of a bank account holder, but can also include corporations, institutions, or even cash. Because paper checks do not need to specify an account, but rather use an abstract name as the recipient of funds, they are very flexible payment instruments. Bitcoin transactions use a similar abstraction, the bitcoin address, to make them very flexible. A bitcoin address can represent the owner of a private/public key pair, or it can represent something else, such as a payment script, as we will see in [p2sh]. For now, let’s examine the simple case, a bitcoin address that represents, and is derived from, a public key.
The bitcoin address is derived from the public key through the use of one-way cryptographic hashing. A "hashing algorithm" or simply "hash algorithm" is a one-way function that produces a fingerprint or "hash" of an arbitrary-sized input. Cryptographic hash functions are used extensively in bitcoin: in bitcoin addresses, in script addresses, and in the mining Proof-of-Work algorithm. The algorithms used to make a bitcoin address from a public key are the Secure Hash Algorithm (SHA) and the RACE Integrity Primitives Evaluation Message Digest (RIPEMD), specifically SHA256 and RIPEMD160.
Starting with the public key K, we compute the SHA256 hash and then compute the RIPEMD160 hash of the result, producing a 160-bit (20-byte) number:
where K is the public key and A is the resulting bitcoin address.
|
Tip
|
A bitcoin address is not the same as a public key. Bitcoin addresses are derived from a public key using a one-way function. |
Bitcoin addresses are almost always encoded as "Base58Check" (see [base58]), which uses 58 characters (a Base58 number system) and a checksum to help human readability, avoid ambiguity, and protect against errors in address transcription and entry. Base58Check is also used in many other ways in bitcoin, whenever there is a need for a user to read and correctly transcribe a number, such as a bitcoin address, a private key, an encrypted key, or a script hash. In the next section we will examine the mechanics of Base58Check encoding and decoding and the resulting representations. [pubkey_to_address] illustrates the conversion of a public key into a bitcoin address.
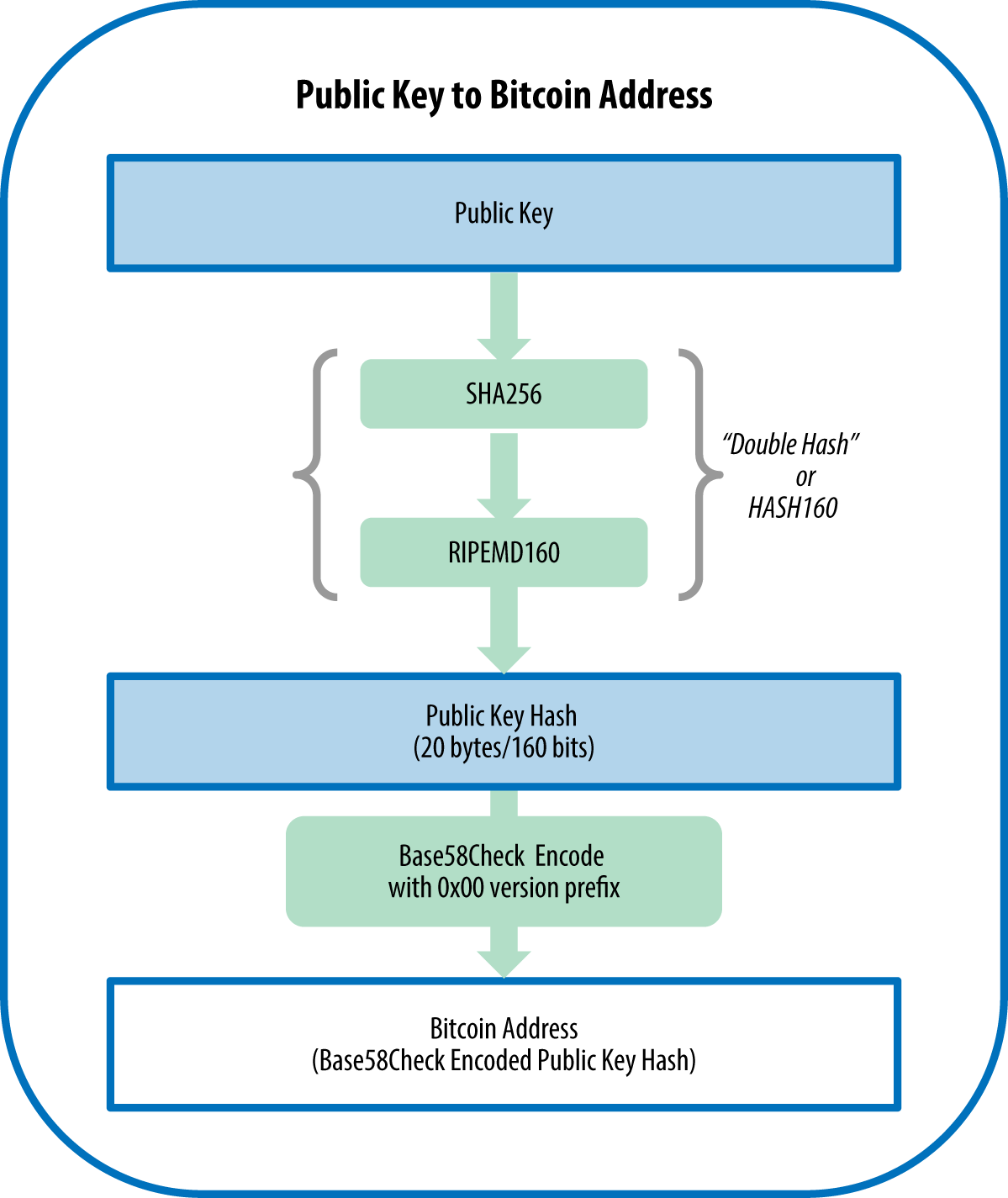
Base58 and Base58Check Encoding
In order to represent long numbers in a compact way, using fewer symbols, many computer systems use mixed-alphanumeric representations with a base (or radix) higher than 10. For example, whereas the traditional decimal system uses the 10 numerals 0 through 9, the hexadecimal system uses 16, with the letters A through F as the six additional symbols. A number represented in hexadecimal format is shorter than the equivalent decimal representation. Even more compact, Base64 representation uses 26 lowercase letters, 26 capital letters, 10 numerals, and 2 more characters such as “+” and "/" to transmit binary data over text-based media such as email. Base64 is most commonly used to add binary attachments to email. Base58 is a text-based binary-encoding format developed for use in bitcoin and used in many other cryptocurrencies. It offers a balance between compact representation, readability, and error detection and prevention. Base58 is a subset of Base64, using upper- and lowercase letters and numbers, but omitting some characters that are frequently mistaken for one another and can appear identical when displayed in certain fonts. Specifically, Base58 is Base64 without the 0 (number zero), O (capital o), l (lower L), I (capital i), and the symbols “+” and "/". Or, more simply, it is a set of lowercase and capital letters and numbers without the four (0, O, l, I) just mentioned. [base58alphabet] shows the full Base58 alphabet.
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyzTo add extra security against typos or transcription errors, Base58Check is a Base58 encoding format, frequently used in bitcoin, which has a built-in error-checking code. The checksum is an additional four bytes added to the end of the data that is being encoded. The checksum is derived from the hash of the encoded data and can therefore be used to detect and prevent transcription and typing errors. When presented with Base58Check code, the decoding software will calculate the checksum of the data and compare it to the checksum included in the code. If the two do not match, an error has been introduced and the Base58Check data is invalid. This prevents a mistyped bitcoin address from being accepted by the wallet software as a valid destination, an error that would otherwise result in loss of funds.
To convert data (a number) into a Base58Check format, we first add a prefix to the data, called the "version byte," which serves to easily identify the type of data that is encoded. For example, in the case of a bitcoin address the prefix is zero (0x00 in hex), whereas the prefix used when encoding a private key is 128 (0x80 in hex). A list of common version prefixes is shown in [base58check_versions].
Next, we compute the "double-SHA" checksum, meaning we apply the SHA256 hash-algorithm twice on the previous result (prefix and data):
checksum = SHA256(SHA256(prefix+data))From the resulting 32-byte hash (hash-of-a-hash), we take only the first four bytes. These four bytes serve as the error-checking code, or checksum. The checksum is concatenated (appended) to the end.
The result is composed of three items: a prefix, the data, and a checksum. This result is encoded using the Base58 alphabet described previously. [base58check_encoding] illustrates the Base58Check encoding process.
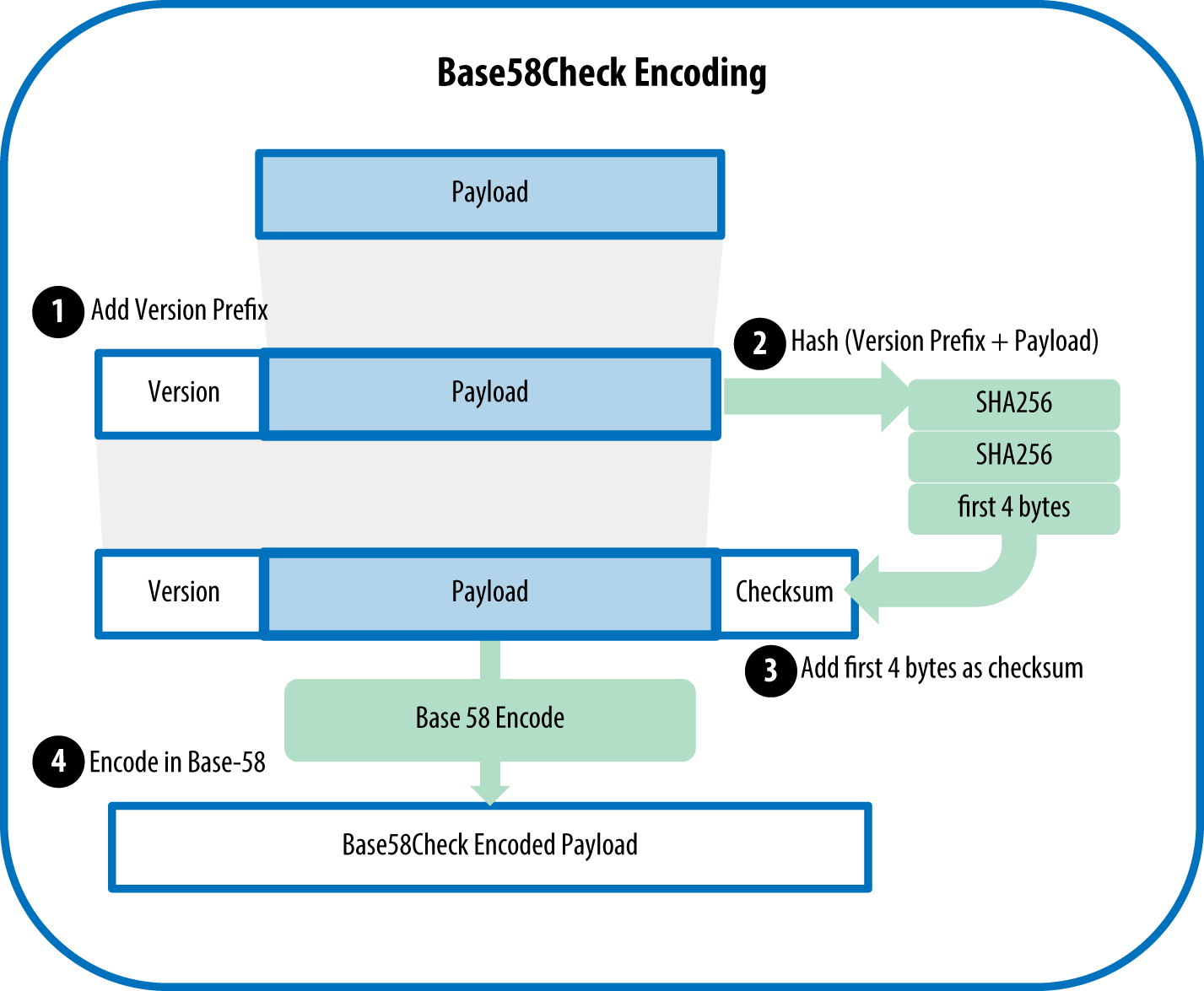
In bitcoin, most of the data presented to the user is Base58Check-encoded to make it compact, easy to read, and easy to detect errors. The version prefix in Base58Check encoding is used to create easily distinguishable formats, which when encoded in Base58 contain specific characters at the beginning of the Base58Check-encoded payload. These characters make it easy for humans to identify the type of data that is encoded and how to use it. This is what differentiates, for example, a Base58Check-encoded bitcoin address that starts with a 1 from a Base58Check-encoded private key WIF that starts with a 5. Some example version prefixes and the resulting Base58 characters are shown in [base58check_versions].
| Type | Version prefix (hex) | Base58 result prefix |
|---|---|---|
Bitcoin Address |
0x00 |
1 |
Pay-to-Script-Hash Address |
0x05 |
3 |
Bitcoin Testnet Address |
0x6F |
m or n |
Private Key WIF |
0x80 |
5, K, or L |
BIP-38 Encrypted Private Key |
0x0142 |
6P |
BIP-32 Extended Public Key |
0x0488B21E |
xpub |
Let’s look at the complete process of creating a bitcoin address, from a private key, to a public key (a point on the elliptic curve), to a double-hashed address, and finally, the Base58Check encoding. The C++ code in [addr_example] shows the complete step-by-step process, from private key to Base58Check-encoded bitcoin address. The code example uses the libbitcoin library introduced in [alt_libraries] for some helper functions.
#include <bitcoin/bitcoin.hpp> int main() { // Private secret key. bc::ec_secret secret; bool success = bc::decode_base16(secret, "038109007313a5807b2eccc082c8c3fbb988a973cacf1a7df9ce725c31b14776"); assert(success); // Get public key. bc::ec_point public_key = bc::secret_to_public_key(secret); std::cout << "Public key: " << bc::encode_hex(public_key) << std::endl; // Create Bitcoin address. // Normally you can use: // bc::payment_address payaddr; // bc::set_public_key(payaddr, public_key); // const std::string address = payaddr.encoded(); // Compute hash of public key for P2PKH address. const bc::short_hash hash = bc::bitcoin_short_hash(public_key); bc::data_chunk unencoded_address; // Reserve 25 bytes // [ version:1 ] // [ hash:20 ] // [ checksum:4 ] unencoded_address.reserve(25); // Version byte, 0 is normal BTC address (P2PKH). unencoded_address.push_back(0); // Hash data bc::extend_data(unencoded_address, hash); // Checksum is computed by hashing data, and adding 4 bytes from hash. bc::append_checksum(unencoded_address); // Finally we must encode the result in Bitcoin's base58 encoding. assert(unencoded_address.size() == 25); const std::string address = bc::encode_base58(unencoded_address); std::cout << "Address: " << address << std::endl; return 0; }
The code uses a predefined private key to produce the same bitcoin address every time it is run, as shown in [addr_example_run].
# Compile the addr.cpp code $ g++ -o addr addr.cpp $(pkg-config --cflags --libs libbitcoin) # Run the addr executable $ ./addr Public key: 0202a406624211f2abbdc68da3df929f938c3399dd79fac1b51b0e4ad1d26a47aa Address: 1PRTTaJesdNovgne6Ehcdu1fpEdX7913CK
Key Formats
Both private and public keys can be represented in a number of different formats. These representations all encode the same number, even though they look different. These formats are primarily used to make it easy for people to read and transcribe keys without introducing errors.
Private key formats
The private key can be represented in a number of different formats, all of which correspond to the same 256-bit number. [table_4-2] shows three common formats used to represent private keys. Different formats are used in different circumstances. Hexadecimal and raw binary formats are used internally in software and rarely shown to users. The WIF is used for import/export of keys between wallets and often used in QR code (barcode) representations of private keys.
| Type | Prefix | Description |
|---|---|---|
Raw |
None |
32 bytes |
Hex |
None |
64 hexadecimal digits |
WIF |
5 |
Base58Check encoding: Base58 with version prefix of 128- and 32-bit checksum |
WIF-compressed |
K or L |
As above, with added suffix 0x01 before encoding |
[table_4-3] shows the private key generated in these three formats.
| Format | Private key |
|---|---|
Hex |
1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd |
WIF |
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
WIF-compressed |
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
All of these representations are different ways of showing the same number, the same private key. They look different, but any one format can easily be converted to any other format. Note that the "raw binary" is not shown in [table_4-3] as any encoding for display here would, by definition, not be raw binary data.
We use the wif-to-ec command from Bitcoin Explorer (see [appdx_bx]) to show that both WIF keys represent the same private key:
$ bx wif-to-ec 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
$ bx wif-to-ec KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aeddDecode from Base58Check
The Bitcoin Explorer commands (see [appdx_bx]) make it easy to write shell scripts and command-line "pipes" that manipulate bitcoin keys, addresses, and transactions. You can use Bitcoin Explorer to decode the Base58Check format on the command line.
We use the base58check-decode command to decode the uncompressed key:
$ bx base58check-decode 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
wrapper
{
checksum 4286807748
payload 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
version 128
}The result contains the key as payload, the WIF version prefix 128, and a checksum.
Notice that the "payload" of the compressed key is appended with the suffix 01, signalling that the derived public key is to be compressed:
$ bx base58check-decode KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
wrapper
{
checksum 2339607926
payload 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd01
version 128
}Encode from hex to Base58Check
To encode into Base58Check (the opposite of the previous command), we use the base58check-encode command from Bitcoin Explorer (see [appdx_bx]) and provide the hex private key, followed by the WIF version prefix 128:
bx base58check-encode 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd --version 128
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1JcnEncode from hex (compressed key) to Base58Check
To encode into Base58Check as a "compressed" private key (see [comp_priv]), we append the suffix 01 to the hex key and then encode as in the preceding section:
$ bx base58check-encode 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd01 --version 128
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJThe resulting WIF-compressed format starts with a "K." This denotes that the private key within has a suffix of "01" and will be used to produce compressed public keys only (see [comp_pub]).
Public key formats
Public keys are also presented in different ways, usually as either compressed or uncompressed public keys.
As we saw previously, the public key is a point on the elliptic curve consisting of a pair of coordinates (x,y). It is usually presented with the prefix 04 followed by two 256-bit numbers: one for the x coordinate of the point, the other for the y coordinate. The prefix 04 is used to distinguish uncompressed public keys from compressed public keys that begin with a 02 or a 03.
Here’s the public key generated by the private key we created earlier, shown as the coordinates x and y:
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDBHere’s the same public key shown as a 520-bit number (130 hex digits) with the prefix 04 followed by x and then y coordinates, as 04 x y:
K = 04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A↵ 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
Compressed public keys
Compressed public keys were introduced to bitcoin to reduce the size of transactions and conserve disk space on nodes that store the bitcoin blockchain database. Most transactions include the public key, which is required to validate the owner’s credentials and spend the bitcoin. Each public key requires 520 bits (prefix + x + y), which when multiplied by several hundred transactions per block, or tens of thousands of transactions per day, adds a significant amount of data to the blockchain.
As we saw in the section [pubkey], a public key is a point (x,y) on an elliptic curve. Because the curve expresses a mathematical function, a point on the curve represents a solution to the equation and, therefore, if we know the x coordinate we can calculate the y coordinate by solving the equation y2 mod p = (x3 + 7) mod p. That allows us to store only the x coordinate of the public key point, omitting the y coordinate and reducing the size of the key and the space required to store it by 256 bits. An almost 50% reduction in size in every transaction adds up to a lot of data saved over time!
Whereas uncompressed public keys have a prefix of 04, compressed public keys start with either a 02 or a 03 prefix. Let’s look at why there are two possible prefixes: because the left side of the equation is y2, the solution for y is a square root, which can have a positive or negative value. Visually, this means that the resulting y coordinate can be above or below the x-axis. As you can see from the graph of the elliptic curve in [ecc-curve], the curve is symmetric, meaning it is reflected like a mirror by the x-axis. So, while we can omit the y coordinate we have to store the sign of y (positive or negative); or in other words, we have to remember if it was above or below the x-axis because each of those options represents a different point and a different public key. When calculating the elliptic curve in binary arithmetic on the finite field of prime order p, the y coordinate is either even or odd, which corresponds to the positive/negative sign as explained earlier. Therefore, to distinguish between the two possible values of y, we store a compressed public key with the prefix 02 if the y is even, and 03 if it is odd, allowing the software to correctly deduce the y coordinate from the x coordinate and uncompress the public key to the full coordinates of the point. Public key compression is illustrated in [pubkey_compression].
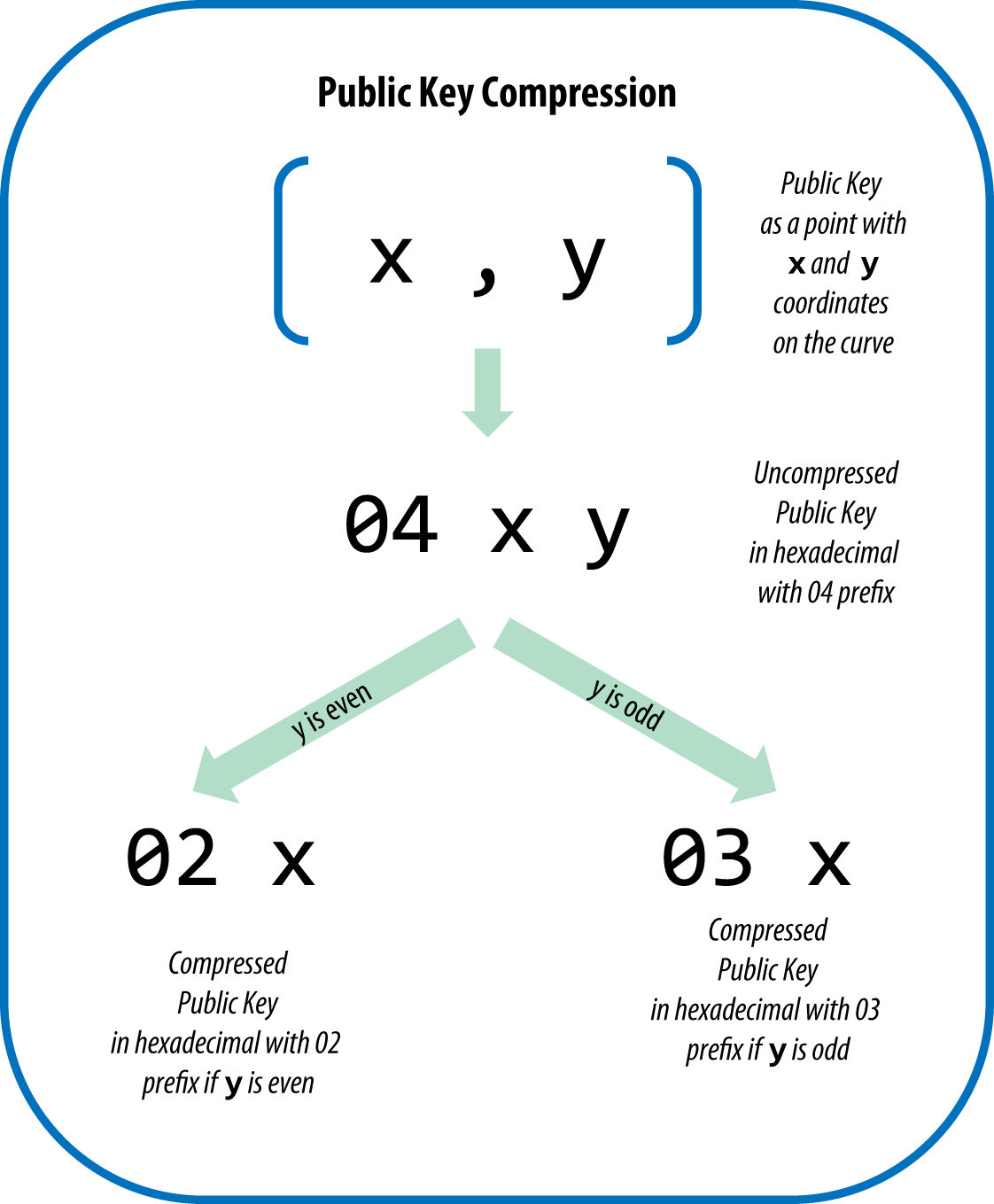
Here’s the same public key generated previously, shown as a compressed public key stored in 264 bits (66 hex digits) with the prefix 03 indicating the y coordinate is odd:
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341AThis compressed public key corresponds to the same private key, meaning it is generated from the same private key. However, it looks different from the uncompressed public key. More importantly, if we convert this compressed public key to a bitcoin address using the double-hash function (RIPEMD160(SHA256(K))) it will produce a different bitcoin address. This can be confusing, because it means that a single private key can produce a public key expressed in two different formats (compressed and uncompressed) that produce two different bitcoin addresses. However, the private key is identical for both bitcoin addresses.
Compressed public keys are gradually becoming the default across bitcoin clients, which is having a significant impact on reducing the size of transactions and therefore the blockchain. However, not all clients support compressed public keys yet. Newer clients that support compressed public keys have to account for transactions from older clients that do not support compressed public keys. This is especially important when a wallet application is importing private keys from another bitcoin wallet application, because the new wallet needs to scan the blockchain to find transactions corresponding to these imported keys. Which bitcoin addresses should the bitcoin wallet scan for? The bitcoin addresses produced by uncompressed public keys, or the bitcoin addresses produced by compressed public keys? Both are valid bitcoin addresses, and can be signed for by the private key, but they are different addresses!
To resolve this issue, when private keys are exported from a wallet, the WIF that is used to represent them is implemented differently in newer bitcoin wallets, to indicate that these private keys have been used to produce compressed public keys and therefore compressed bitcoin addresses. This allows the importing wallet to distinguish between private keys originating from older or newer wallets and search the blockchain for transactions with bitcoin addresses corresponding to the uncompressed, or the compressed, public keys, respectively. Let’s look at how this works in more detail, in the next section.
Compressed private keys
Ironically, the term "compressed private key" is a misnomer, because when a private key is exported as WIF-compressed it is actually one byte longer than an "uncompressed" private key. That is because the private key has an added one-byte suffix (shown as 01 in hex in [table_4-4]), which signifies that the private key is from a newer wallet and should only be used to produce compressed public keys. Private keys are not themselves compressed and cannot be compressed. The term "compressed private key" really means "private key from which only compressed public keys should be derived," whereas "uncompressed private key" really means "private key from which only uncompressed public keys should be derived." You should only refer to the export format as "WIF-compressed" or "WIF" and not refer to the private key itself as "compressed" to avoid further confusion
[table_4-4] shows the same key, encoded in WIF and WIF-compressed formats.
| Format | Private key |
|---|---|
Hex |
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD |
WIF |
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
Hex-compressed |
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD01 |
WIF-compressed |
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
Notice that the hex-compressed private key format has one extra byte at the end (01 in hex). While the Base58 encoding version prefix is the same (0x80) for both WIF and WIF-compressed formats, the addition of one byte on the end of the number causes the first character of the Base58 encoding to change from a 5 to either a K or L. Think of this as the Base58 equivalent of the decimal encoding difference between the number 100 and the number 99. While 100 is one digit longer than 99, it also has a prefix of 1 instead of a prefix of 9. As the length changes, it affects the prefix. In Base58, the prefix 5 changes to a K or L as the length of the number increases by one byte.
Remember, these formats are not used interchangeably. In a newer wallet that implements compressed public keys, the private keys will only ever be exported as WIF-compressed (with a K or L prefix). If the wallet is an older implementation and does not use compressed public keys, the private keys will only ever be exported as WIF (with a 5 prefix). The goal here is to signal to the wallet importing these private keys whether it must search the blockchain for compressed or uncompressed public keys and addresses.
If a bitcoin wallet is able to implement compressed public keys, it will use those in all transactions. The private keys in the wallet will be used to derive the public key points on the curve, which will be compressed. The compressed public keys will be used to produce bitcoin addresses and those will be used in transactions. When exporting private keys from a new wallet that implements compressed public keys, the WIF is modified, with the addition of a one-byte suffix 01 to the private key. The resulting Base58Check-encoded private key is called a "compressed WIF" and starts with the letter K or L, instead of starting with "5" as is the case with WIF-encoded (noncompressed) keys from older wallets.
|
Tip
|
"Compressed private keys" is a misnomer! They are not compressed; rather, WIF-compressed signifies that the keys should only be used to derive compressed public keys and their corresponding bitcoin addresses. Ironically, a "WIF-compressed" encoded private key is one byte longer because it has the added |
Implementing Keys and Addresses in Python
The most comprehensive bitcoin library in Python is pybitcointools by Vitalik Buterin. In [key-to-address_script], we use the pybitcointools library (imported as "bitcoin") to generate and display keys and addresses in various formats.
import bitcoin # Generate a random private key valid_private_key = False while not valid_private_key: private_key = bitcoin.random_key() decoded_private_key = bitcoin.decode_privkey(private_key, 'hex') valid_private_key = 0 < decoded_private_key < bitcoin.N print "Private Key (hex) is: ", private_key print "Private Key (decimal) is: ", decoded_private_key # Convert private key to WIF format wif_encoded_private_key = bitcoin.encode_privkey(decoded_private_key, 'wif') print "Private Key (WIF) is: ", wif_encoded_private_key # Add suffix "01" to indicate a compressed private key compressed_private_key = private_key + '01' print "Private Key Compressed (hex) is: ", compressed_private_key # Generate a WIF format from the compressed private key (WIF-compressed) wif_compressed_private_key = bitcoin.encode_privkey( bitcoin.decode_privkey(compressed_private_key, 'hex'), 'wif') print "Private Key (WIF-Compressed) is: ", wif_compressed_private_key # Multiply the EC generator point G with the private key to get a public key point public_key = bitcoin.fast_multiply(bitcoin.G, decoded_private_key) print "Public Key (x,y) coordinates is:", public_key # Encode as hex, prefix 04 hex_encoded_public_key = bitcoin.encode_pubkey(public_key,'hex') print "Public Key (hex) is:", hex_encoded_public_key # Compress public key, adjust prefix depending on whether y is even or odd (public_key_x, public_key_y) = public_key if (public_key_y % 2) == 0: compressed_prefix = '02' else: compressed_prefix = '03' hex_compressed_public_key = compressed_prefix + bitcoin.encode(public_key_x, 16) print "Compressed Public Key (hex) is:", hex_compressed_public_key # Generate bitcoin address from public key print "Bitcoin Address (b58check) is:", bitcoin.pubkey_to_address(public_key) # Generate compressed bitcoin address from compressed public key print "Compressed Bitcoin Address (b58check) is:", \ bitcoin.pubkey_to_address(hex_compressed_public_key)
[key-to-address_script_run] shows the output from running this code.
$ python key-to-address-ecc-example.py Private Key (hex) is: 3aba4162c7251c891207b747840551a71939b0de081f85c4e44cf7c13e41daa6 Private Key (decimal) is: 26563230048437957592232553826663696440606756685920117476832299673293013768870 Private Key (WIF) is: 5JG9hT3beGTJuUAmCQEmNaxAuMacCTfXuw1R3FCXig23RQHMr4K Private Key Compressed (hex) is: 3aba4162c7251c891207b747840551a71939b0de081f85c4e44cf7c13e41daa601 Private Key (WIF-Compressed) is: KyBsPXxTuVD82av65KZkrGrWi5qLMah5SdNq6uftawDbgKa2wv6S Public Key (x,y) coordinates is: (41637322786646325214887832269588396900663353932545912953362782457239403430124L, 16388935128781238405526710466724741593761085120864331449066658622400339362166L) Public Key (hex) is: 045c0de3b9c8ab18dd04e3511243ec2952002dbfadc864b9628910169d9b9b00ec↵ 243bcefdd4347074d44bd7356d6a53c495737dd96295e2a9374bf5f02ebfc176 Compressed Public Key (hex) is: 025c0de3b9c8ab18dd04e3511243ec2952002dbfadc864b9628910169d9b9b00ec Bitcoin Address (b58check) is: 1thMirt546nngXqyPEz532S8fLwbozud8 Compressed Bitcoin Address (b58check) is: 14cxpo3MBCYYWCgF74SWTdcmxipnGUsPw3
[ec_math] is another example, using the Python ECDSA library for the elliptic curve math and without using any specialized bitcoin libraries.
import ecdsa import os from ecdsa.util import string_to_number, number_to_string # secp256k1, http://www.oid-info.com/get/1.3.132.0.10 _p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2FL _r = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141L _b = 0x0000000000000000000000000000000000000000000000000000000000000007L _a = 0x0000000000000000000000000000000000000000000000000000000000000000L _Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798L _Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8L curve_secp256k1 = ecdsa.ellipticcurve.CurveFp(_p, _a, _b) generator_secp256k1 = ecdsa.ellipticcurve.Point(curve_secp256k1, _Gx, _Gy, _r) oid_secp256k1 = (1, 3, 132, 0, 10) SECP256k1 = ecdsa.curves.Curve("SECP256k1", curve_secp256k1, generator_secp256k1, oid_secp256k1) ec_order = _r curve = curve_secp256k1 generator = generator_secp256k1 def random_secret(): convert_to_int = lambda array: int("".join(array).encode("hex"), 16) # Collect 256 bits of random data from the OS's cryptographically secure random generator byte_array = os.urandom(32) return convert_to_int(byte_array) def get_point_pubkey(point): if point.y() & 1: key = '03' + '%064x' % point.x() else: key = '02' + '%064x' % point.x() return key.decode('hex') def get_point_pubkey_uncompressed(point): key = '04' + \ '%064x' % point.x() + \ '%064x' % point.y() return key.decode('hex') # Generate a new private key. secret = random_secret() print "Secret: ", secret # Get the public key point. point = secret * generator print "EC point:", point print "BTC public key:", get_point_pubkey(point).encode("hex") # Given the point (x, y) we can create the object using: point1 = ecdsa.ellipticcurve.Point(curve, point.x(), point.y(), ec_order) assert point1 == point
[ec_math_run] shows the output produced by running this script.
|
Note
|
[ec_math] uses |
$ # Install Python PIP package manager
$ sudo apt-get install python-pip
$ # Install the Python ECDSA library
$ sudo pip install ecdsa
$ # Run the script
$ python ec-math.py
Secret: 38090835015954358862481132628887443905906204995912378278060168703580660294000
EC point: (70048853531867179489857750497606966272382583471322935454624595540007269312627, 105262206478686743191060800263479589329920209527285803935736021686045542353380)
BTC public key: 029ade3effb0a67d5c8609850d797366af428f4a0d5194cb221d807770a1522873Advanced Keys and Addresses
In the following sections we will look at advanced forms of keys and addresses, such as encrypted private keys, script and multisignature addresses, vanity addresses, and paper wallets.
Encrypted Private Keys (BIP-38)
Private keys must remain secret. The need for confidentiality of the private keys is a truism that is quite difficult to achieve in practice, because it conflicts with the equally important security objective of availability. Keeping the private key private is much harder when you need to store backups of the private key to avoid losing it. A private key stored in a wallet that is encrypted by a password might be secure, but that wallet needs to be backed up. At times, users need to move keys from one wallet to another—to upgrade or replace the wallet software, for example. Private key backups might also be stored on paper (see [paper_wallets]) or on external storage media, such as a USB flash drive. But what if the backup itself is stolen or lost? These conflicting security goals led to the introduction of a portable and convenient standard for encrypting private keys in a way that can be understood by many different wallets and bitcoin clients, standardized by BIP-38 (see [appdxbitcoinimpproposals]).
BIP-38 proposes a common standard for encrypting private keys with a passphrase and encoding them with Base58Check so that they can be stored securely on backup media, transported securely between wallets, or kept in any other conditions where the key might be exposed. The standard for encryption uses the Advanced Encryption Standard (AES), a standard established by the NIST and used broadly in data encryption implementations for commercial and military applications.
A BIP-38 encryption scheme takes as input a bitcoin private key, usually encoded in the WIF, as a Base58Check string with the prefix of "5." Additionally, the BIP-38 encryption scheme takes a passphrase—a long password—usually composed of several words or a complex string of alphanumeric characters. The result of the BIP-38 encryption scheme is a Base58Check-encoded encrypted private key that begins with the prefix 6P. If you see a key that starts with 6P, it is encrypted and requires a passphrase in order to convert (decrypt) it back into a WIF-formatted private key (prefix 5) that can be used in any wallet. Many wallet applications now recognize BIP-38-encrypted private keys and will prompt the user for a passphrase to decrypt and import the key. Third-party applications, such as the incredibly useful browser-based Bit Address (Wallet Details tab), can be used to decrypt BIP-38 keys.
The most common use case for BIP-38 encrypted keys is for paper wallets that can be used to back up private keys on a piece of paper. As long as the user selects a strong passphrase, a paper wallet with BIP-38 encrypted private keys is incredibly secure and a great way to create offline bitcoin storage (also known as "cold storage").
Test the encrypted keys in [table_4-10] using bitaddress.org to see how you can get the decrypted key by entering the passphrase.
Private Key (WIF) |
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
Passphrase |
MyTestPassphrase |
Encrypted Key (BIP-38) |
6PRTHL6mWa48xSopbU1cKrVjpKbBZxcLRRCdctLJ3z5yxE87MobKoXdTsJ |
Pay-to-Script Hash (P2SH) and Multisig Addresses
As we know, traditional bitcoin addresses begin with the number “1” and are derived from the public key, which is derived from the private key. Although anyone can send bitcoin to a “1” address, that bitcoin can only be spent by presenting the corresponding private key signature and public key hash.
Bitcoin addresses that begin with the number “3” are pay-to-script hash (P2SH) addresses, sometimes erroneously called multisignature or multisig addresses. They designate the beneficiary of a bitcoin transaction as the hash of a script, instead of the owner of a public key. The feature was introduced in January 2012 with BIP-16 (see [appdxbitcoinimpproposals]), and is being widely adopted because it provides the opportunity to add functionality to the address itself. Unlike transactions that "send" funds to traditional “1” bitcoin addresses, also known as a pay-to-public-key-hash (P2PKH), funds sent to “3” addresses require something more than the presentation of one public key hash and one private key signature as proof of ownership. The requirements are designated at the time the address is created, within the script, and all inputs to this address will be encumbered with the same requirements.
A P2SH address is created from a transaction script, which defines who can spend a transaction output (for more details, see [p2sh]). Encoding a P2SH address involves using the same double-hash function as used during creation of a bitcoin address, only applied on the script instead of the public key:
script hash = RIPEMD160(SHA256(script))The resulting "script hash" is encoded with Base58Check with a version prefix of 5, which results in an encoded address starting with a 3. An example of a P2SH address is 3F6i6kwkevjR7AsAd4te2YB2zZyASEm1HM, which can be derived using the Bitcoin Explorer commands script-encode, sha256, ripemd160, and base58check-encode (see [appdx_bx]) as follows:
$ echo dup hash160 [ 89abcdefabbaabbaabbaabbaabbaabbaabbaabba ] equalverify checksig > script
$ bx script-encode < script | bx sha256 | bx ripemd160 | bx base58check-encode --version 5
3F6i6kwkevjR7AsAd4te2YB2zZyASEm1HM|
Tip
|
P2SH is not necessarily the same as a multisignature standard transaction. A P2SH address most often represents a multi-signature script, but it might also represent a script encoding other types of transactions. |
Multisignature addresses and P2SH
Currently, the most common implementation of the P2SH function is the multi-signature address script. As the name implies, the underlying script requires more than one signature to prove ownership and therefore spend funds. The bitcoin multi-signature feature is designed to require M signatures (also known as the “threshold”) from a total of N keys, known as an M-of-N multisig, where M is equal to or less than N. For example, Bob the coffee shop owner from [ch01_intro_what_is_bitcoin] could use a multisignature address requiring 1-of-2 signatures from a key belonging to him and a key belonging to his spouse, ensuring either of them could sign to spend a transaction output locked to this address. This would be similar to a “joint account” as implemented in traditional banking where either spouse can spend with a single signature. Or Gopesh, the web designer paid by Bob to create a website, might have a 2-of-3 multisignature address for his business that ensures that no funds can be spent unless at least two of the business partners sign a transaction.
We will explore how to create transactions that spend funds from P2SH (and multi-signature) addresses in [transactions].
Vanity Addresses
Vanity addresses are valid bitcoin addresses that contain human-readable messages. For example, 1LoveBPzzD72PUXLzCkYAtGFYmK5vYNR33 is a valid address that contains the letters forming the word "Love" as the first four Base-58 letters. Vanity addresses require generating and testing billions of candidate private keys, until a bitcoin address with the desired pattern is found. Although there are some optimizations in the vanity generation algorithm, the process essentially involves picking a private key at random, deriving the public key, deriving the bitcoin address, and checking to see if it matches the desired vanity pattern, repeating billions of times until a match is found.
Once a vanity address matching the desired pattern is found, the private key from which it was derived can be used by the owner to spend bitcoin in exactly the same way as any other address. Vanity addresses are no less or more secure than any other address. They depend on the same Elliptic Curve Cryptography (ECC) and SHA as any other address. You can no more easily find the private key of an address starting with a vanity pattern than you can any other address.
In [ch01_intro_what_is_bitcoin], we introduced Eugenia, a children’s charity director operating in the Philippines. Let’s say that Eugenia is organizing a bitcoin fundraising drive and wants to use a vanity bitcoin address to publicize the fundraising. Eugenia will create a vanity address that starts with "1Kids" to promote the children’s charity fundraiser. Let’s see how this vanity address will be created and what it means for the security of Eugenia’s charity.
Generating vanity addresses
It’s important to realize that a bitcoin address is simply a number represented by symbols in the Base58 alphabet. The search for a pattern like "1Kids" can be seen as searching for an address in the range from 1Kids11111111111111111111111111111 to 1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz. There are approximately 5829 (approximately 1.4 * 1051) addresses in that range, all starting with "1Kids." [table_4-11] shows the range of addresses that have the prefix 1Kids.
From |
|
|
|
|
|
|
|
To |
|
Let’s look at the pattern "1Kids" as a number and see how frequently we might find this pattern in a bitcoin address (see [table_4-12]). An average desktop computer PC, without any specialized hardware, can search approximately 100,000 keys per second.
| Length | Pattern | Frequency | Average search time |
|---|---|---|---|
1 |
1K |
1 in 58 keys |
< 1 milliseconds |
2 |
1Ki |
1 in 3,364 |
50 milliseconds |
3 |
1Kid |
1 in 195,000 |
< 2 seconds |
4 |
1Kids |
1 in 11 million |
1 minute |
5 |
1KidsC |
1 in 656 million |
1 hour |
6 |
1KidsCh |
1 in 38 billion |
2 days |
7 |
1KidsCha |
1 in 2.2 trillion |
3–4 months |
8 |
1KidsChar |
1 in 128 trillion |
13–18 years |
9 |
1KidsChari |
1 in 7 quadrillion |
800 years |
10 |
1KidsCharit |
1 in 400 quadrillion |
46,000 years |
11 |
1KidsCharity |
1 in 23 quintillion |
2.5 million years |
As you can see, Eugenia won’t be creating the vanity address "1KidsCharity" anytime soon, even if she had access to several thousand computers. Each additional character increases the difficulty by a factor of 58. Patterns with more than seven characters are usually found by specialized hardware, such as custom-built desktops with multiple GPUs. These are often repurposed bitcoin mining "rigs" that are no longer profitable for bitcoin mining but can be used to find vanity addresses. Vanity searches on GPU systems are many orders of magnitude faster than on a general-purpose CPU.
Another way to find a vanity address is to outsource the work to a pool of vanity miners, such as the pool at Vanity Pool. A pool is a service that allows those with GPU hardware to earn bitcoin searching for vanity addresses for others. For a small payment (0.01 bitcoin or approximately $5 at the time of this writing), Eugenia can outsource the search for a seven-character pattern vanity address and get results in a few hours instead of having to run a CPU search for months.
Generating a vanity address is a brute-force exercise: try a random key, check the resulting address to see if it matches the desired pattern, repeat until successful. [vanity_miner_code] shows an example of a "vanity miner," a program designed to find vanity addresses, written in C++. The example uses the libbitcoin library, which we introduced in [alt_libraries].
#include <bitcoin/bitcoin.hpp> // The string we are searching for const std::string search = "1kid"; // Generate a random secret key. A random 32 bytes. bc::ec_secret random_secret(std::default_random_engine& engine); // Extract the Bitcoin address from an EC secret. std::string bitcoin_address(const bc::ec_secret& secret); // Case insensitive comparison with the search string. bool match_found(const std::string& address); int main() { // random_device on Linux uses "/dev/urandom" // CAUTION: Depending on implementation this RNG may not be secure enough! // Do not use vanity keys generated by this example in production std::random_device random; std::default_random_engine engine(random()); // Loop continuously... while (true) { // Generate a random secret. bc::ec_secret secret = random_secret(engine); // Get the address. std::string address = bitcoin_address(secret); // Does it match our search string? (1kid) if (match_found(address)) { // Success! std::cout << "Found vanity address! " << address << std::endl; std::cout << "Secret: " << bc::encode_hex(secret) << std::endl; return 0; } } // Should never reach here! return 0; } bc::ec_secret random_secret(std::default_random_engine& engine) { // Create new secret... bc::ec_secret secret; // Iterate through every byte setting a random value... for (uint8_t& byte: secret) byte = engine() % std::numeric_limits<uint8_t>::max(); // Return result. return secret; } std::string bitcoin_address(const bc::ec_secret& secret) { // Convert secret to pubkey... bc::ec_point pubkey = bc::secret_to_public_key(secret); // Finally create address. bc::payment_address payaddr; bc::set_public_key(payaddr, pubkey); // Return encoded form. return payaddr.encoded(); } bool match_found(const std::string& address) { auto addr_it = address.begin(); // Loop through the search string comparing it to the lower case // character of the supplied address. for (auto it = search.begin(); it != search.end(); ++it, ++addr_it) if (*it != std::tolower(*addr_it)) return false; // Reached end of search string, so address matches. return true; }
|
Note
|
[vanity_miner_run] uses |
The example code must be compiled using a C++ compiler and linked against the libbitcoin library (which must be first installed on that system). To run the example, run the vanity-miner executable with no parameters (see [vanity_miner_run]) and it will attempt to find a vanity address starting with "1kid."
$ # Compile the code with g++ $ g++ -o vanity-miner vanity-miner.cpp $(pkg-config --cflags --libs libbitcoin) $ # Run the example $ ./vanity-miner Found vanity address! 1KiDzkG4MxmovZryZRj8tK81oQRhbZ46YT Secret: 57cc268a05f83a23ac9d930bc8565bac4e277055f4794cbd1a39e5e71c038f3f $ # Run it again for a different result $ ./vanity-miner Found vanity address! 1Kidxr3wsmMzzouwXibKfwTYs5Pau8TUFn Secret: 7f65bbbbe6d8caae74a0c6a0d2d7b5c6663d71b60337299a1a2cf34c04b2a623 # Use "time" to see how long it takes to find a result $ time ./vanity-miner Found vanity address! 1KidPWhKgGRQWD5PP5TAnGfDyfWp5yceXM Secret: 2a802e7a53d8aa237cd059377b616d2bfcfa4b0140bc85fa008f2d3d4b225349 real 0m8.868s user 0m8.828s sys 0m0.035s
The example code will take a few seconds to find a match for the three-character pattern "kid," as we can see when we use the time Unix command to measure the execution time. Change the search pattern in the source code and see how much longer it takes for four- or five-character patterns!
Vanity address security
Vanity addresses can be used to enhance and to defeat security measures; they are truly a double-edged sword. Used to improve security, a distinctive address makes it harder for adversaries to substitute their own address and fool your customers into paying them instead of you. Unfortunately, vanity addresses also make it possible for anyone to create an address that resembles any random address, or even another vanity address, thereby fooling your customers.
Eugenia could advertise a randomly generated address (e.g., 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy) to which people can send their donations. Or, she could generate a vanity address that starts with 1Kids, to make it more distinctive.
In both cases, one of the risks of using a single fixed address (rather than a separate dynamic address per donor) is that a thief might be able to infiltrate your website and replace it with his own address, thereby diverting donations to himself. If you have advertised your donation address in a number of different places, your users may visually inspect the address before making a payment to ensure it is the same one they saw on your website, on your email, and on your flyer. In the case of a random address like 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy, the average user will perhaps inspect the first few characters "1J7mdg" and be satisfied that the address matches. Using a vanity address generator, someone with the intent to steal by substituting a similar-looking address can quickly generate addresses that match the first few characters, as shown in [table_4-13].
Original Random Address |
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy |
Vanity (4-character match) |
1J7md1QqU4LpctBetHS2ZoyLV5d6dShhEy |
Vanity (5-character match) |
1J7mdgYqyNd4ya3UEcq31Q7sqRMXw2XZ6n |
Vanity (6-character match) |
1J7mdg5WxGENmwyJP9xuGhG5KRzu99BBCX |
So does a vanity address increase security? If Eugenia generates the vanity address 1Kids33q44erFfpeXrmDSz7zEqG2FesZEN, users are likely to look at the vanity pattern word and a few characters beyond, for example noticing the "1Kids33" part of the address. That would force an attacker to generate a vanity address matching at least six characters (two more), expending an effort that is 3,364 times (58 × 58) higher than the effort Eugenia expended for her 4-character vanity. Essentially, the effort Eugenia expends (or pays a vanity pool for) "pushes" the attacker into having to produce a longer pattern vanity. If Eugenia pays a pool to generate an 8-character vanity address, the attacker would be pushed into the realm of 10 characters, which is infeasible on a personal computer and expensive even with a custom vanity-mining rig or vanity pool. What is affordable for Eugenia becomes unaffordable for the attacker, especially if the potential reward of fraud is not high enough to cover the cost of the vanity address generation.
Paper Wallets
Paper wallets are bitcoin private keys printed on paper. Often the paper wallet also includes the corresponding bitcoin address for convenience, but this is not necessary because it can be derived from the private key. Paper wallets are a very effective way to create backups or offline bitcoin storage, also known as "cold storage." As a backup mechanism, a paper wallet can provide security against the loss of key due to a computer mishap such as a hard-drive failure, theft, or accidental deletion. As a "cold storage" mechanism, if the paper wallet keys are generated offline and never stored on a computer system, they are much more secure against hackers, keyloggers, and other online computer threats.
Paper wallets come in many shapes, sizes, and designs, but at a very basic level are just a key and an address printed on paper. [table_4-14] shows the simplest form of a paper wallet.
| Public address | Private key (WIF) |
|---|---|
1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62x |
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
Paper wallets can be generated easily using a tool such as the client-side JavaScript generator at bitaddress.org. This page contains all the code necessary to generate keys and paper wallets, even while completely disconnected from the internet. To use it, save the HTML page on your local drive or on an external USB flash drive. Disconnect from the internet and open the file in a browser. Even better, boot your computer using a pristine operating system, such as a CD-ROM bootable Linux OS. Any keys generated with this tool while offline can be printed on a local printer over a USB cable (not wirelessly), thereby creating paper wallets whose keys exist only on the paper and have never been stored on any online system. Put these paper wallets in a fireproof safe and "send" bitcoin to their bitcoin address, to implement a simple yet highly effective "cold storage" solution. [paper_wallet_simple] shows a paper wallet generated from the bitaddress.org site.

The disadvantage of a simple paper wallet system is that the printed keys are vulnerable to theft. A thief who is able to gain access to the paper can either steal it or photograph the keys and take control of the bitcoin locked with those keys. A more sophisticated paper wallet storage system uses BIP-38 encrypted private keys. The keys printed on the paper wallet are protected by a passphrase that the owner has memorized. Without the passphrase, the encrypted keys are useless. Yet, they still are superior to a passphrase-protected wallet because the keys have never been online and must be physically retrieved from a safe or other physically secured storage. [paper_wallet_encrypted] shows a paper wallet with an encrypted private key (BIP-38) created on the bitaddress.org site.

|
Warning
|
Although you can deposit funds into a paper wallet several times, you should withdraw all funds only once, spending everything. This is because in the process of unlocking and spending funds some wallets might generate a change address if you spend less than the whole amount. Additionally, if the computer you use to sign the transaction is compromised, you risk exposing the private key. By spending the entire balance of a paper wallet only once, you reduce the risk of key compromise. If you need only a small amount, send any remaining funds to a new paper wallet in the same transaction. |
Paper wallets come in many designs and sizes, with many different features. Some are intended to be given as gifts and have seasonal themes, such as Christmas and New Year’s themes. Others are designed for storage in a bank vault or safe with the private key hidden in some way, either with opaque scratch-off stickers, or folded and sealed with tamper-proof adhesive foil. Figures #paper_wallet_bpw through #paper_wallet_spw show various examples of paper wallets with security and backup features.
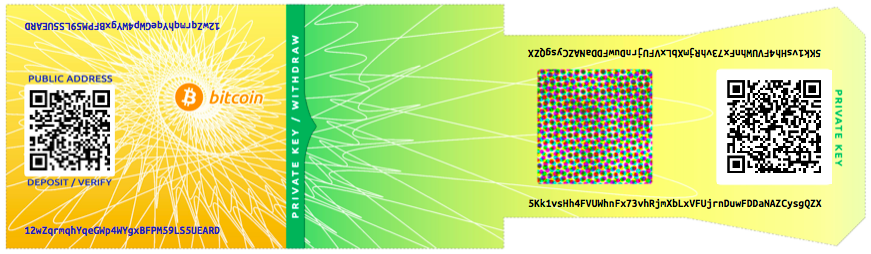

Other designs feature additional copies of the key and address, in the form of detachable stubs similar to ticket stubs, allowing you to store multiple copies to protect against fire, flood, or other natural disasters.

Wallets
The word "wallet" is used to describe a few different things in bitcoin.
At a high level, a wallet is an application that serves as the primary user interface. The wallet controls access to a user’s money, managing keys and addresses, tracking the balance, and creating and signing transactions.
More narrowly, from a programmer’s perspective, the word "wallet" refers to the data structure used to store and manage a user’s keys.
In this chapter we will look at the second meaning, where wallets are containers for private keys, usually implemented as structured files or simple databases.
Wallet Technology Overview
In this section we summarize the various technologies used to construct user-friendly, secure, and flexible bitcoin wallets.
A common misconception about bitcoin is that bitcoin wallets contain bitcoin. In fact, the wallet contains only keys. The "coins" are recorded in the blockchain on the bitcoin network. Users control the coins on the network by signing transactions with the keys in their wallets. In a sense, a bitcoin wallet is a keychain.
|
Tip
|
Bitcoin wallets contain keys, not coins. Each user has a wallet containing keys. Wallets are really keychains containing pairs of private/public keys (see [private_public_keys]). Users sign transactions with the keys, thereby proving they own the transaction outputs (their coins). The coins are stored on the blockchain in the form of transaction outputs (often noted as vout or txout). |
There are two primary types of wallets, distinguished by whether the keys they contain are related to each other or not.
The first type is a nondeterministic wallet, where each key is independently generated from a random number. The keys are not related to each other. This type of wallet is also known as a JBOK wallet from the phrase "Just a Bunch Of Keys."
The second type of wallet is a deterministic wallet, where all the keys are derived from a single master key, known as the seed. All the keys in this type of wallet are related to each other and can be generated again if one has the original seed. There are a number of different key derivation methods used in deterministic wallets. The most commonly used derivation method uses a tree-like structure and is known as a hierarchical deterministic or HD wallet.
Deterministic wallets are initialized from a seed. To make these easier to use, seeds are encoded as English words, also known as mnemonic code words.
The next few sections introduce each of these technologies at a high level.
Nondeterministic (Random) Wallets
In the first bitcoin wallet (now called Bitcoin Core), wallets were collections of randomly generated private keys. For example, the original Bitcoin Core client pregenerates 100 random private keys when first started and generates more keys as needed, using each key only once. Such wallets are being replaced with deterministic wallets because they are cumbersome to manage, back up, and import. The disadvantage of random keys is that if you generate many of them you must keep copies of all of them, meaning that the wallet must be backed up frequently. Each key must be backed up, or the funds it controls are irrevocably lost if the wallet becomes inaccessible. This conflicts directly with the principle of avoiding address reuse, by using each bitcoin address for only one transaction. Address reuse reduces privacy by associating multiple transactions and addresses with each other. A Type-0 nondeterministic wallet is a poor choice of wallet, especially if you want to avoid address reuse because it means managing many keys, which creates the need for frequent backups. Although the Bitcoin Core client includes a Type-0 wallet, using this wallet is discouraged by developers of Bitcoin Core. [Type0_wallet] shows a nondeterministic wallet, containing a loose collection of random keys.
|
Tip
|
The use of nondeterministic wallets is discouraged for anything other than simple tests. They are simply too cumbersome to back up and use. Instead, use an industry-standard–based HD wallet with a mnemonic seed for backup. |
Deterministic (Seeded) Wallets
Deterministic, or "seeded," wallets are wallets that contain private keys that are all derived from a common seed, through the use of a one-way hash function. The seed is a randomly generated number that is combined with other data, such as an index number or "chain code" (see [hd_wallets]) to derive the private keys. In a deterministic wallet, the seed is sufficient to recover all the derived keys, and therefore a single backup at creation time is sufficient. The seed is also sufficient for a wallet export or import, allowing for easy migration of all the user’s keys between different wallet implementations. [Type1_wallet] shows a logical diagram of a deterministic wallet.
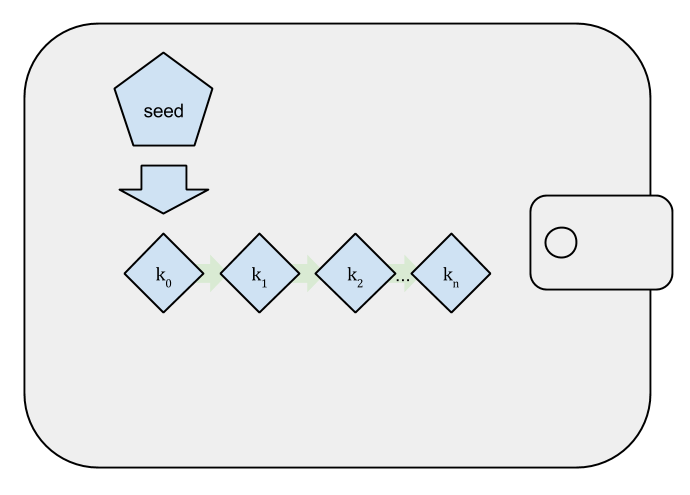
HD Wallets (BIP-32/BIP-44)
Deterministic wallets were developed to make it easy to derive many keys from a single "seed." The most advanced form of deterministic wallets is the HD wallet defined by the BIP-32 standard. HD wallets contain keys derived in a tree structure, such that a parent key can derive a sequence of children keys, each of which can derive a sequence of grandchildren keys, and so on, to an infinite depth. This tree structure is illustrated in [Type2_wallet].
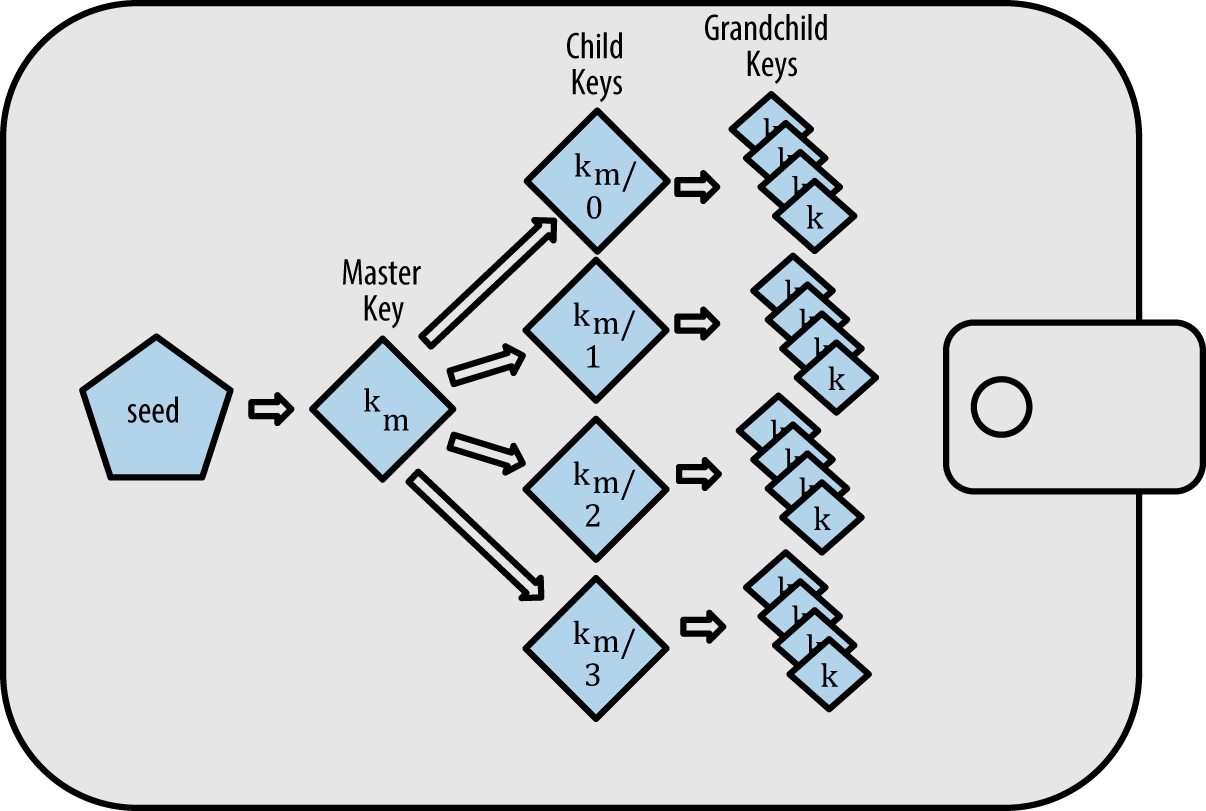
HD wallets offer two major advantages over random (nondeterministic) keys. First, the tree structure can be used to express additional organizational meaning, such as when a specific branch of subkeys is used to receive incoming payments and a different branch is used to receive change from outgoing payments. Branches of keys can also be used in corporate settings, allocating different branches to departments, subsidiaries, specific functions, or accounting categories.
The second advantage of HD wallets is that users can create a sequence of public keys without having access to the corresponding private keys. This allows HD wallets to be used on an insecure server or in a receive-only capacity, issuing a different public key for each transaction. The public keys do not need to be preloaded or derived in advance, yet the server doesn’t have the private keys that can spend the funds.
Seeds and Mnemonic Codes (BIP-39)
HD wallets are a very powerful mechanism for managing many keys and addresses. They are even more useful if they are combined with a standardized way of creating seeds from a sequence of English words that are easy to transcribe, export, and import across wallets. This is known as a mnemonic and the standard is defined by BIP-39. Today, most bitcoin wallets (as well as wallets for other cryptocurrencies) use this standard and can import and export seeds for backup and recovery using interoperable mnemonics.
Let’s look at this from a practical perspective. Which of the following seeds is easier to transcribe, record on paper, read without error, export, and import into another wallet?
0C1E24E5917779D297E14D45F14E1A1Aarmy van defense carry jealous true
garbage claim echo media make crunchWallet Best Practices
As bitcoin wallet technology has matured, certain common industry standards have emerged that make bitcoin wallets broadly interoperable, easy to use, secure, and flexible. These common standards are:
-
Mnemonic code words, based on BIP-39
-
HD wallets, based on BIP-32
-
Multipurpose HD wallet structure, based on BIP-43
-
Multicurrency and multiaccount wallets, based on BIP-44
These standards may change or may become obsolete by future developments, but for now they form a set of interlocking technologies that have become the de facto wallet standard for bitcoin.
The standards have been adopted by a broad range of software and hardware bitcoin wallets, making all these wallets interoperable. A user can export a mnemonic generated on one of these wallets and import it in another wallet, recovering all transactions, keys, and addresses.
Some example of software wallets supporting these standards include (listed alphabetically) Breadwallet, Copay, Multibit HD, and Mycelium. Examples of hardware wallets supporting these standards include (listed alphabetically) Keepkey, Ledger, and Trezor.
The following sections examine each of these technologies in detail.
|
Tip
|
If you are implementing a bitcoin wallet, it should be built as a HD wallet, with a seed encoded as mnemonic code for backup, following the BIP-32, BIP-39, BIP-43, and BIP-44 standards, as described in the following sections. |
Using a Bitcoin Wallet
In [user-stories] we introduced Gabriel, an enterprising young teenager in Rio de Janeiro, who is running a simple web store that sells bitcoin-branded t-shirts, coffee mugs, and stickers.
Gabriel uses a Trezor bitcoin hardware wallet ([a_trezor_device]) to securely manage his bitcoin. The Trezor is a simple USB device with two buttons that stores keys (in the form of an HD wallet) and signs transactions. Trezor wallets implement all the industry standards discussed in this chapter, so Gabriel is not reliant on any proprietary technology or single vendor solution.

When Gabriel used the Trezor for the first time, the device generated a mnemonic and seed from a built-in hardware random number generator. During this initialization phase, the wallet displayed a numbered sequence of words, one by one, on the screen (see [trezor_mnemonic_display]).
By writing down this mnemonic, Gabriel created a backup (see [mnemonic_paper_backup]) that can be used for recovery in the case of loss or damage to the Trezor device. This mnemonic can be used for recovery in a new Trezor or in any one of the many compatible software or hardware wallets. Note that the sequence of words is important, so mnemonic paper backups have numbered spaces for each word. Gabriel had to carefully record each word in the numbered space to preserve the correct sequence.
1. |
army |
7. |
garbage |
2. |
van |
8. |
claim |
3. |
defense |
9. |
echo |
4. |
carry |
10. |
media |
5. |
jealous |
11. |
make |
6. |
true |
12. |
crunch |
|
Note
|
A 12-word mnemonic is shown in [mnemonic_paper_backup], for simplicity. In fact, most hardware wallets generate a more secure 24-word mnemonic. The mnemonic is used in exactly the same way, regardless of length. |
For the first implementation of his web store, Gabriel uses a single bitcoin address, generated on his Trezor device. This single address is used by all customers for all orders. As we will see, this approach has some drawbacks and can be improved upon with an HD wallet.
Wallet Technology Details
Let’s now examine each of the important industry standards that are used by many bitcoin wallets in detail.
Mnemonic Code Words (BIP-39)
Mnemonic code words are word sequences that represent (encode) a random number used as a seed to derive a deterministic wallet. The sequence of words is sufficient to re-create the seed and from there re-create the wallet and all the derived keys. A wallet application that implements deterministic wallets with mnemonic words will show the user a sequence of 12 to 24 words when first creating a wallet. That sequence of words is the wallet backup and can be used to recover and re-create all the keys in the same or any compatible wallet application. Mnemonic words make it easier for users to back up wallets because they are easy to read and correctly transcribe, as compared to a random sequence of numbers.
|
Tip
|
Mnemonic words are often confused with "brainwallets." They are not the same. The primary difference is that a brainwallet consists of words chosen by the user, whereas mnemonic words are created randomly by the wallet and presented to the user. This important difference makes mnemonic words much more secure, because humans are very poor sources of randomness. |
Mnemonic codes are defined in BIP-39 (see [appdxbitcoinimpproposals]). Note that BIP-39 is one implementation of a mnemonic code standard. There is a different standard, with a different set of words, used by the Electrum wallet and predating BIP-39. BIP-39 was proposed by the company behind the Trezor hardware wallet and is incompatible with Electrum’s implementation. However, BIP-39 has now achieved broad industry support across dozens of interoperable implementations and should be considered the de facto industry standard.
BIP-39 defines the creation of a mnemonic code and seed, which we describe here in nine steps. For clarity, the process is split into two parts: steps 1 through 6 are shown in [generating_mnemonic_words] and steps 7 through 9 are shown in [mnemonic_to_seed].
Generating mnemonic words
Mnemonic words are generated automatically by the wallet using the standardized process defined in BIP-39. The wallet starts from a source of entropy, adds a checksum, and then maps the entropy to a word list:
-
Create a random sequence (entropy) of 128 to 256 bits.
-
Create a checksum of the random sequence by taking the first (entropy-length/32) bits of its SHA256 hash.
-
Add the checksum to the end of the random sequence.
-
Divide the sequence into sections of 11 bits.
-
Map each 11-bit value to a word from the predefined dictionary of 2048 words.
-
The mnemonic code is the sequence of words.
[generating_entropy_and_encoding] shows how entropy is used to generate mnemonic words.
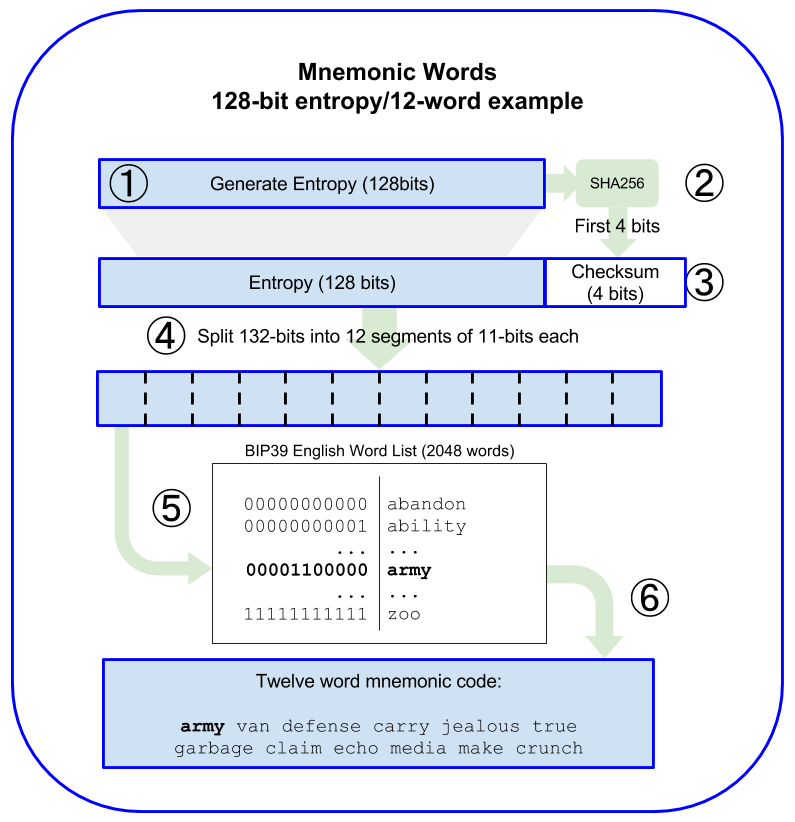
[table_4-5] shows the relationship between the size of the entropy data and the length of mnemonic codes in words.
| Entropy (bits) | Checksum (bits) | Entropy + checksum (bits) | Mnemonic length (words) |
|---|---|---|---|
128 |
4 |
132 |
12 |
160 |
5 |
165 |
15 |
192 |
6 |
198 |
18 |
224 |
7 |
231 |
21 |
256 |
8 |
264 |
24 |
From mnemonic to seed
The mnemonic words represent entropy with a length of 128 to 256 bits. The entropy is then used to derive a longer (512-bit) seed through the use of the key-stretching function PBKDF2. The seed produced is then used to build a deterministic wallet and derive its keys.
The key-stretching function takes two parameters: the mnemonic and a salt. The purpose of a salt in a key-stretching function is to make it difficult to build a lookup table enabling a brute-force attack. In the BIP-39 standard, the salt has another purpose—it allows the introduction of a passphrase that serves as an additional security factor protecting the seed, as we will describe in more detail in [mnemonic_passphrase].
The process described in steps 7 through 9 continues from the process described previously in [generating_mnemonic_words]:
- The first parameter to the PBKDF2 key-stretching function is the mnemonic produced from step 6.
- The second parameter to the PBKDF2 key-stretching function is a salt. The salt is composed of the string constant "
mnemonic" concatenated with an optional user-supplied passphrase string. - PBKDF2 stretches the mnemonic and salt parameters using 2048 rounds of hashing with the HMAC-SHA512 algorithm, producing a 512-bit value as its final output. That 512-bit value is the seed.
[fig_5_7] shows how a mnemonic is used to generate a seed.
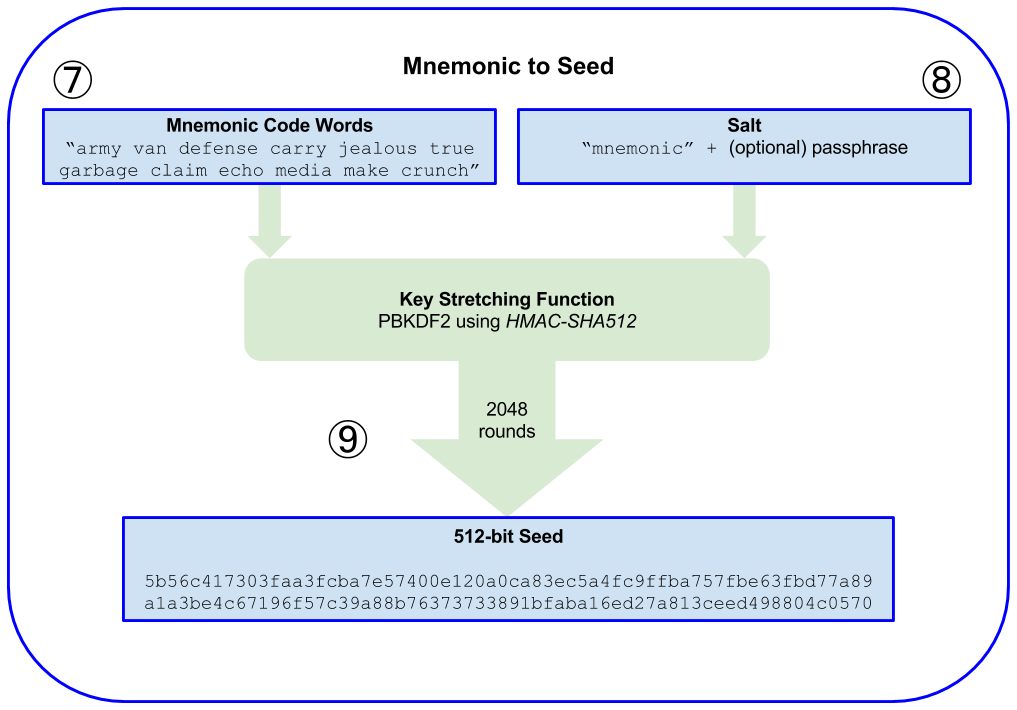
|
Tip
|
The key-stretching function, with its 2048 rounds of hashing, is a very effective protection against brute-force attacks against the mnemonic or the passphrase. It makes it extremely costly (in computation) to try more than a few thousand passphrase and mnemonic combinations, while the number of possible derived seeds is vast (2512). |
Tables #mnemonic_128_no_pass, #mnemonic_128_w_pass, and #mnemonic_256_no_pass show some examples of mnemonic codes and the seeds they produce (without any passphrase).
Entropy input (128 bits) |
|
Mnemonic (12 words) |
|
Passphrase |
(none) |
Seed (512 bits) |
|
Entropy input (128 bits) |
|
Mnemonic (12 words) |
|
Passphrase |
SuperDuperSecret |
Seed (512 bits) |
|
Entropy input (256 bits) |
|
Mnemonic (24 words) |
|
Passphrase |
(none) |
Seed (512 bits) |
|
Optional passphrase in BIP-39
The BIP-39 standard allows the use of an optional passphrase in the derivation of the seed. If no passphrase is used, the mnemonic is stretched with a salt consisting of the constant string "mnemonic", producing a specific 512-bit seed from any given mnemonic. If a passphrase is used, the stretching function produces a different seed from that same mnemonic. In fact, given a single mnemonic, every possible passphrase leads to a different seed. Essentially, there is no "wrong" passphrase. All passphrases are valid and they all lead to different seeds, forming a vast set of possible uninitialized wallets. The set of possible wallets is so large (2512) that there is no practical possibility of brute-forcing or accidentally guessing one that is in use.
|
Tip
|
There are no "wrong" passphrases in BIP-39. Every passphrase leads to some wallet, which unless previously used will be empty. |
The optional passphrase creates two important features:
-
A second factor (something memorized) that makes a mnemonic useless on its own, protecting mnemonic backups from compromise by a thief.
-
A form of plausible deniability or "duress wallet," where a chosen passphrase leads to a wallet with a small amount of funds used to distract an attacker from the "real" wallet that contains the majority of funds.
However, it is important to note that the use of a passphrase also introduces the risk of loss:
-
If the wallet owner is incapacitated or dead and no one else knows the passphrase, the seed is useless and all the funds stored in the wallet are lost forever.
-
Conversely, if the owner backs up the passphrase in the same place as the seed, it defeats the purpose of a second factor.
While passphrases are very useful, they should only be used in combination with a carefully planned process for backup and recovery, considering the possibility of surviving the owner and allowing his or her family to recover the cryptocurrency estate.
Working with mnemonic codes
BIP-39 is implemented as a library in many different programming languages:
- python-mnemonic
-
The reference implementation of the standard by the SatoshiLabs team that proposed BIP-39, in Python
- bitcoinjs/bip39
-
An implementation of BIP-39, as part of the popular bitcoinJS framework, in JavaScript
- libbitcoin/mnemonic
-
An implementation of BIP-39, as part of the popular Libbitcoin framework, in C++
There is also a BIP-39 generator implemented in a standalone webpage, which is extremely useful for testing and experimentation. [a_bip39_generator_as_a_standalone_web_page] shows a standalone web page that generates mnemonics, seeds, and extended private keys.
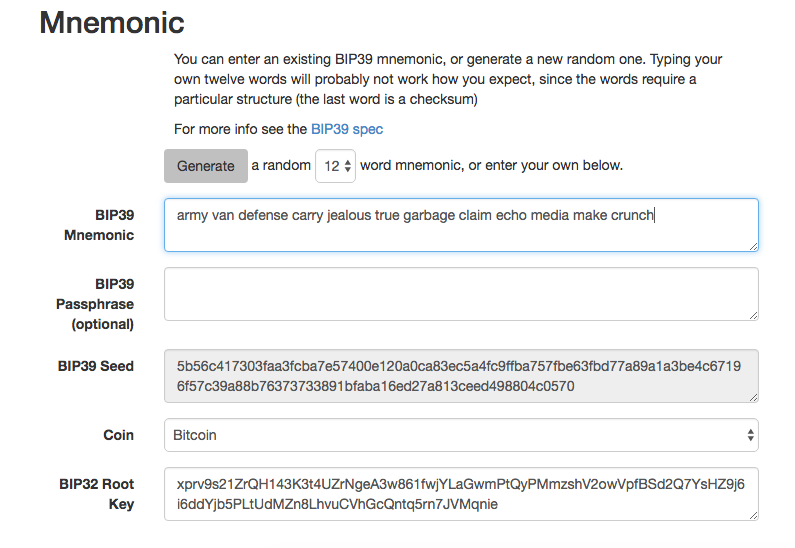
The page can be used offline in a browser, or accessed online.
Creating an HD Wallet from the Seed
HD wallets are created from a single root seed, which is a 128-, 256-, or 512-bit random number. Most commonly, this seed is generated from a mnemonic as detailed in the previous section.
Every key in the HD wallet is deterministically derived from this root seed, which makes it possible to re-create the entire HD wallet from that seed in any compatible HD wallet. This makes it easy to back up, restore, export, and import HD wallets containing thousands or even millions of keys by simply transferring only the mnemonic that the root seed is derived from.
The process of creating the master keys and master chain code for an HD wallet is shown in [HDWalletFromSeed].
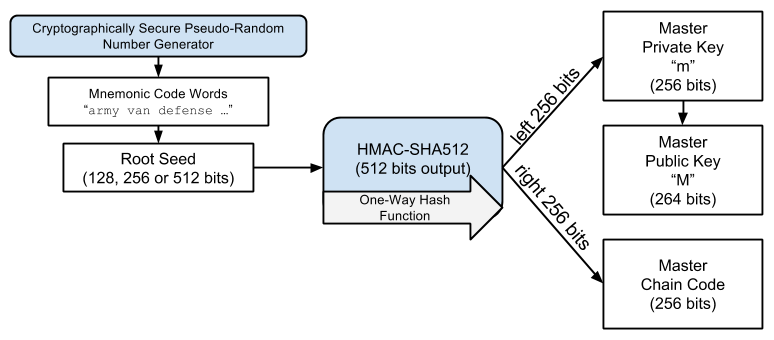
The root seed is input into the HMAC-SHA512 algorithm and the resulting hash is used to create a master private key (m) and a master chain code (c).
The master private key (m) then generates a corresponding master public key (M) using the normal elliptic curve multiplication process m * G that we saw in [pubkey].
The chain code (c) is used to introduce entropy in the function that creates child keys from parent keys, as we will see in the next section.
Private child key derivation
HD wallets use a child key derivation (CKD) function to derive child keys from parent keys.
The child key derivation functions are based on a one-way hash function that combines:
-
A parent private or public key (ECDSA uncompressed key)
-
A seed called a chain code (256 bits)
-
An index number (32 bits)
The chain code is used to introduce deterministic random data to the process, so that knowing the index and a child key is not sufficient to derive other child keys. Knowing a child key does not make it possible to find its siblings, unless you also have the chain code. The initial chain code seed (at the root of the tree) is made from the seed, while subsequent child chain codes are derived from each parent chain code.
These three items (parent key, chain code, and index) are combined and hashed to generate children keys, as follows.
The parent public key, chain code, and the index number are combined and hashed with the HMAC-SHA512 algorithm to produce a 512-bit hash. This 512-bit hash is split into two 256-bit halves. The right-half 256 bits of the hash output become the chain code for the child. The left-half 256 bits of the hash and the index number are added to the parent private key to produce the child private key. In [CKDpriv], we see this illustrated with the index set to 0 to produce the "zero" (first by index) child of the parent.
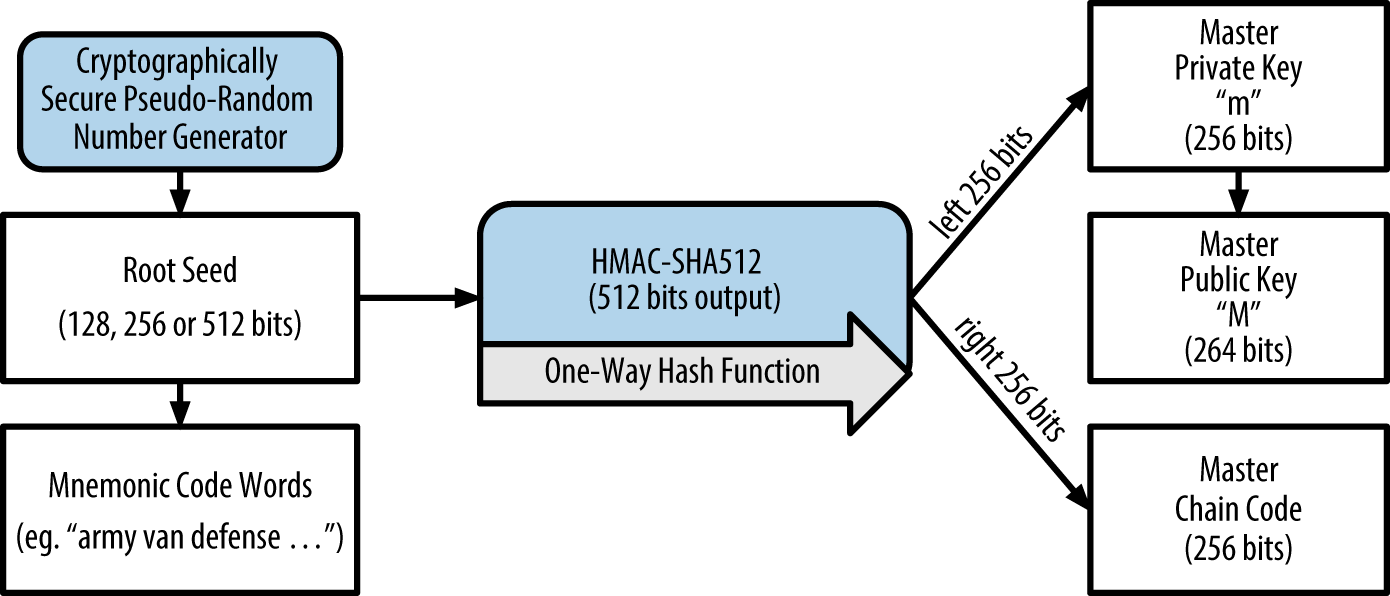
Changing the index allows us to extend the parent and create the other children in the sequence, e.g., Child 0, Child 1, Child 2, etc. Each parent key can have 2,147,483,647 (231) children (231 is half of the entire 232 range available because the other half is reserved for a special type of derivation we will talk about later in this chapter).
Repeating the process one level down the tree, each child can in turn become a parent and create its own children, in an infinite number of generations.
Using derived child keys
Child private keys are indistinguishable from nondeterministic (random) keys. Because the derivation function is a one-way function, the child key cannot be used to find the parent key. The child key also cannot be used to find any siblings. If you have the nth child, you cannot find its siblings, such as the n–1 child or the n+1 child, or any other children that are part of the sequence. Only the parent key and chain code can derive all the children. Without the child chain code, the child key cannot be used to derive any grandchildren either. You need both the child private key and the child chain code to start a new branch and derive grandchildren.
So what can the child private key be used for on its own? It can be used to make a public key and a bitcoin address. Then, it can be used to sign transactions to spend anything paid to that address.
|
Tip
|
A child private key, the corresponding public key, and the bitcoin address are all indistinguishable from keys and addresses created randomly. The fact that they are part of a sequence is not visible outside of the HD wallet function that created them. Once created, they operate exactly as "normal" keys. |
Extended keys
As we saw earlier, the key derivation function can be used to create children at any level of the tree, based on the three inputs: a key, a chain code, and the index of the desired child. The two essential ingredients are the key and chain code, and combined these are called an extended key. The term "extended key" could also be thought of as "extensible key" because such a key can be used to derive children.
Extended keys are stored and represented simply as the concatenation of the 256-bit key and 256-bit chain code into a 512-bit sequence. There are two types of extended keys. An extended private key is the combination of a private key and chain code and can be used to derive child private keys (and from them, child public keys). An extended public key is a public key and chain code, which can be used to create child public keys (public only), as described in [public_key_derivation].
Think of an extended key as the root of a branch in the tree structure of the HD wallet. With the root of the branch, you can derive the rest of the branch. The extended private key can create a complete branch, whereas the extended public key can only create a branch of public keys.
|
Tip
|
An extended key consists of a private or public key and chain code. An extended key can create children, generating its own branch in the tree structure. Sharing an extended key gives access to the entire branch. |
Extended keys are encoded using Base58Check, to easily export and import between different BIP-32–compatible wallets. The Base58Check coding for extended keys uses a special version number that results in the prefix "xprv" and "xpub" when encoded in Base58 characters to make them easily recognizable. Because the extended key is 512 or 513 bits, it is also much longer than other Base58Check-encoded strings we have seen previously.
Here’s an example of an extended private key, encoded in Base58Check:
xprv9tyUQV64JT5qs3RSTJkXCWKMyUgoQp7F3hA1xzG6ZGu6u6Q9VMNjGr67Lctvy5P8oyaYAL9CAWrUE9i6GoNMKUga5biW6Hx4tws2six3b9cHere’s the corresponding extended public key, encoded in Base58Check:
xpub67xpozcx8pe95XVuZLHXZeG6XWXHpGq6Qv5cmNfi7cS5mtjJ2tgypeQbBs2UAR6KECeeMVKZBPLrtJunSDMstweyLXhRgPxdp14sk9tJPW9Public child key derivation
As mentioned previously, a very useful characteristic of HD wallets is the ability to derive public child keys from public parent keys, without having the private keys. This gives us two ways to derive a child public key: either from the child private key, or directly from the parent public key.
An extended public key can be used, therefore, to derive all of the public keys (and only the public keys) in that branch of the HD wallet structure.
This shortcut can be used to create very secure public key–only deployments where a server or application has a copy of an extended public key and no private keys whatsoever. That kind of deployment can produce an infinite number of public keys and bitcoin addresses, but cannot spend any of the money sent to those addresses. Meanwhile, on another, more secure server, the extended private key can derive all the corresponding private keys to sign transactions and spend the money.
One common application of this solution is to install an extended public key on a web server that serves an ecommerce application. The web server can use the public key derivation function to create a new bitcoin address for every transaction (e.g., for a customer shopping cart). The web server will not have any private keys that would be vulnerable to theft. Without HD wallets, the only way to do this is to generate thousands of bitcoin addresses on a separate secure server and then preload them on the ecommerce server. That approach is cumbersome and requires constant maintenance to ensure that the ecommerce server doesn’t "run out" of keys.
Another common application of this solution is for cold-storage or hardware wallets. In that scenario, the extended private key can be stored on a paper wallet or hardware device (such as a Trezor hardware wallet), while the extended public key can be kept online. The user can create "receive" addresses at will, while the private keys are safely stored offline. To spend the funds, the user can use the extended private key on an offline signing bitcoin client or sign transactions on the hardware wallet device (e.g., Trezor). [CKDpub] illustrates the mechanism for extending a parent public key to derive child public keys.
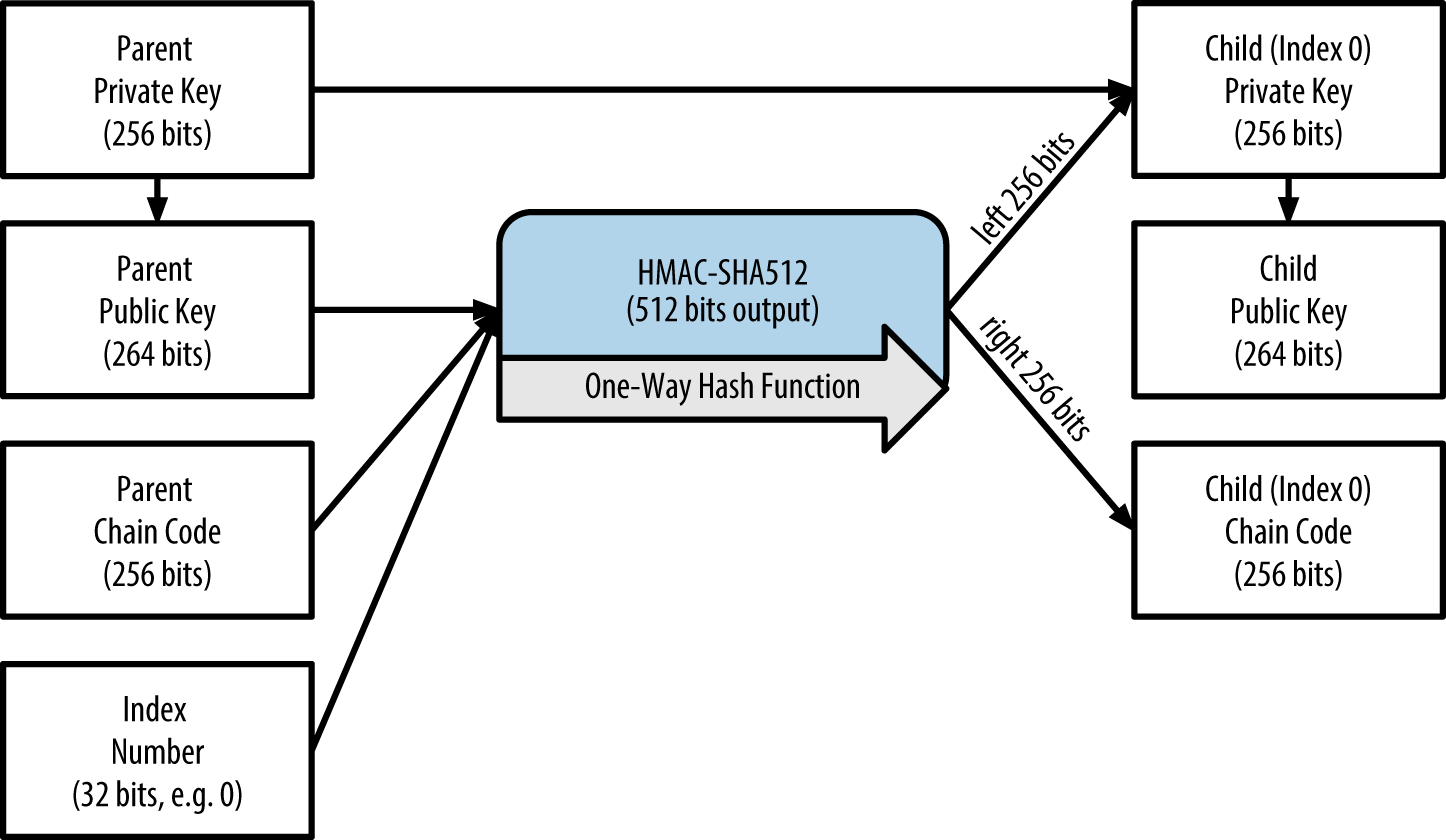
Using an Extended Public Key on a Web Store
Let’s see how HD wallets are used by continuing our story with Gabriel’s web store.
Gabriel first set up his web store as a hobby, based on a simple hosted Wordpress page. His store was quite basic with only a few pages and an order form with a single bitcoin address.
Gabriel used the first bitcoin address generated by his Trezor device as the main bitcoin address for his store. This way, all incoming payments would be paid to an address controlled by his Trezor hardware wallet.
Customers would submit an order using the form and send payment to Gabriel’s published bitcoin address, triggering an email with the order details for Gabriel to process. With just a few orders each week, this system worked well enough.
However, the little web store became quite successful and attracted many orders from the local community. Soon, Gabriel was overwhelmed. With all the orders paying the same address, it became difficult to correctly match orders and transactions, especially when multiple orders for the same amount came in close together.
Gabriel’s HD wallet offers a much better solution through the ability to derive public child keys without knowing the private keys. Gabriel can load an extended public key (xpub) on his website, which can be used to derive a unique address for every customer order. Gabriel can spend the funds from his Trezor, but the xpub loaded on the website can only generate addresses and receive funds. This feature of HD wallets is a great security feature. Gabriel’s website does not contain any private keys and therefore does not need high levels of security.
To export the xpub, Gabriel uses the web-based software in conjunction with the Trezor hardware wallet. The Trezor device must be plugged in for the public keys to be exported. Note that hardware wallets will never export private keys—those always remain on the device. [export_xpub] shows the web interface Gabriel uses to export the xpub.
Gabriel copies the xpub to his web store’s bitcoin shop software. He uses Mycelium Gear, which is an open source web-store plugin for a variety of web hosting and content platforms. Mycelium Gear uses the xpub to generate a unique address for every purchase.
Hardened child key derivation
The ability to derive a branch of public keys from an xpub is very useful, but it comes with a potential risk. Access to an xpub does not give access to child private keys. However, because the xpub contains the chain code, if a child private key is known, or somehow leaked, it can be used with the chain code to derive all the other child private keys. A single leaked child private key, together with a parent chain code, reveals all the private keys of all the children. Worse, the child private key together with a parent chain code can be used to deduce the parent private key.
To counter this risk, HD wallets use an alternative derivation function called hardened derivation, which "breaks" the relationship between parent public key and child chain code. The hardened derivation function uses the parent private key to derive the child chain code, instead of the parent public key. This creates a "firewall" in the parent/child sequence, with a chain code that cannot be used to compromise a parent or sibling private key. The hardened derivation function looks almost identical to the normal child private key derivation, except that the parent private key is used as input to the hash function, instead of the parent public key, as shown in the diagram in [CKDprime].
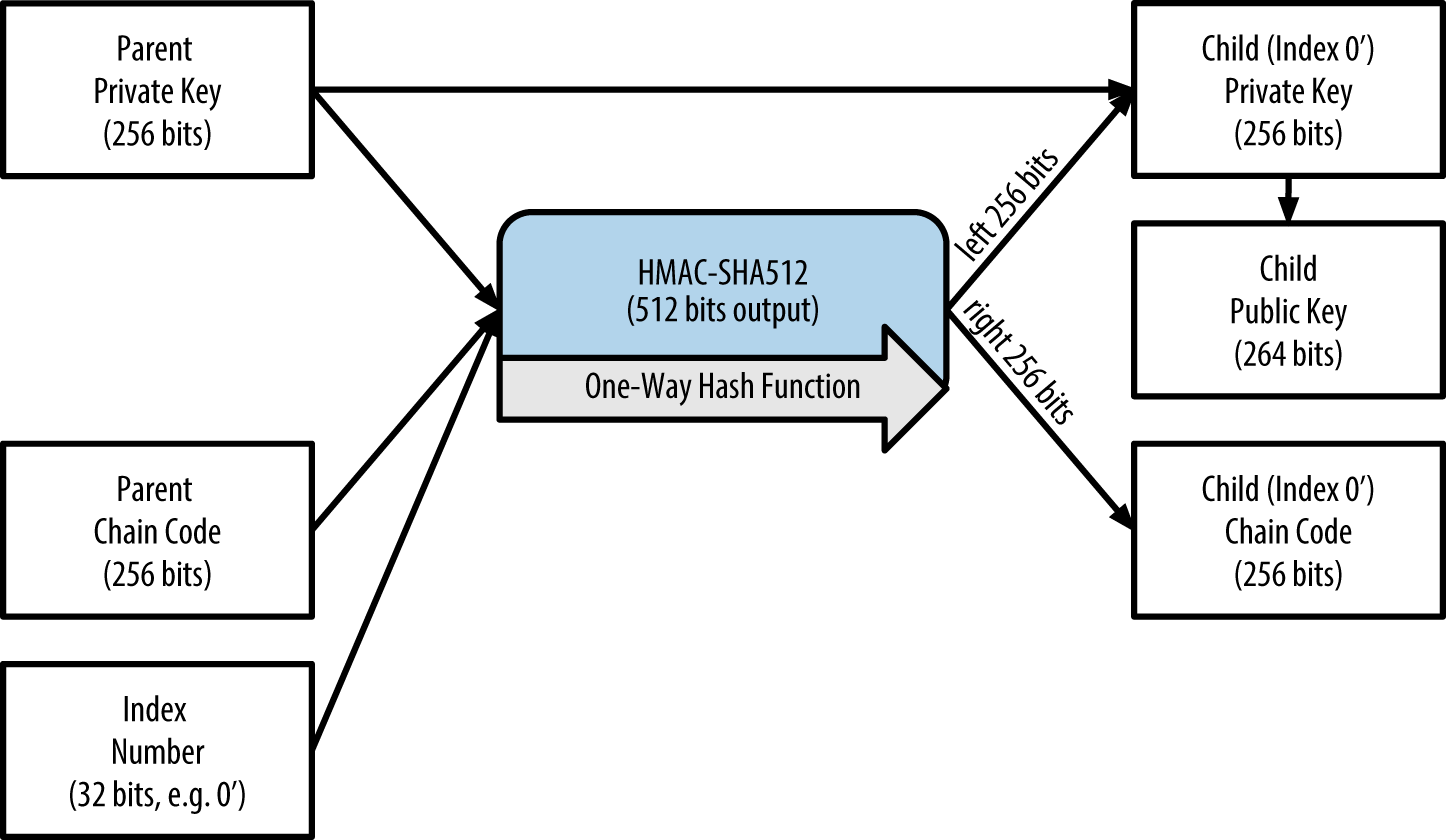
When the hardened private derivation function is used, the resulting child private key and chain code are completely different from what would result from the normal derivation function. The resulting "branch" of keys can be used to produce extended public keys that are not vulnerable, because the chain code they contain cannot be exploited to reveal any private keys. Hardened derivation is therefore used to create a "gap" in the tree above the level where extended public keys are used.
In simple terms, if you want to use the convenience of an xpub to derive branches of public keys, without exposing yourself to the risk of a leaked chain code, you should derive it from a hardened parent, rather than a normal parent. As a best practice, the level-1 children of the master keys are always derived through the hardened derivation, to prevent compromise of the master keys.
Index numbers for normal and hardened derivation
The index number used in the derivation function is a 32-bit integer. To easily distinguish between keys derived through the normal derivation function versus keys derived through hardened derivation, this index number is split into two ranges. Index numbers between 0 and 231–1 (0x0 to 0x7FFFFFFF) are used only for normal derivation. Index numbers between 231 and 232–1 (0x80000000 to 0xFFFFFFFF) are used only for hardened derivation. Therefore, if the index number is less than 231, the child is normal, whereas if the index number is equal or above 231, the child is hardened.
To make the index number easier to read and display, the index number for hardened children is displayed starting from zero, but with a prime symbol. The first normal child key is therefore displayed as 0, whereas the first hardened child (index 0x80000000) is displayed as 0'. In sequence then, the second hardened key would have index 0x80000001 and would be displayed as 1', and so on. When you see an HD wallet index i', that means 231+i.
HD wallet key identifier (path)
Keys in an HD wallet are identified using a "path" naming convention, with each level of the tree separated by a slash (/) character (see [table_4-8]). Private keys derived from the master private key start with "m." Public keys derived from the master public key start with "M." Therefore, the first child private key of the master private key is m/0. The first child public key is M/0. The second grandchild of the first child is m/0/1, and so on.
The "ancestry" of a key is read from right to left, until you reach the master key from which it was derived. For example, identifier m/x/y/z describes the key that is the z-th child of key m/x/y, which is the y-th child of key m/x, which is the x-th child of m.
| HD path | Key described |
|---|---|
m/0 |
The first (0) child private key from the master private key (m) |
m/0/0 |
The first grandchild private key of the first child (m/0) |
m/0'/0 |
The first normal grandchild of the first hardened child (m/0') |
m/1/0 |
The first grandchild private key of the second child (m/1) |
M/23/17/0/0 |
The first great-great-grandchild public key of the first great-grandchild of the 18th grandchild of the 24th child |
Navigating the HD wallet tree structure
The HD wallet tree structure offers tremendous flexibility. Each parent extended key can have 4 billion children: 2 billion normal children and 2 billion hardened children. Each of those children can have another 4 billion children, and so on. The tree can be as deep as you want, with an infinite number of generations. With all that flexibility, however, it becomes quite difficult to navigate this infinite tree. It is especially difficult to transfer HD wallets between implementations, because the possibilities for internal organization into branches and subbranches are endless.
Two BIPs offer a solution to this complexity by creating some proposed standards for the structure of HD wallet trees. BIP-43 proposes the use of the first hardened child index as a special identifier that signifies the "purpose" of the tree structure. Based on BIP-43, an HD wallet should use only one level-1 branch of the tree, with the index number identifying the structure and namespace of the rest of the tree by defining its purpose. For example, an HD wallet using only branch m/i'/ is intended to signify a specific purpose and that purpose is identified by index number "i."
Extending that specification, BIP-44 proposes a multiaccount structure as "purpose" number 44' under BIP-43. All HD wallets following the BIP-44 structure are identified by the fact that they only used one branch of the tree: m/44'/.
BIP-44 specifies the structure as consisting of five predefined tree levels:
m / purpose' / coin_type' / account' / change / address_indexThe first-level "purpose" is always set to 44'. The second-level "coin_type" specifies the type of cryptocurrency coin, allowing for multicurrency HD wallets where each currency has its own subtree under the second level. There are three currencies defined for now: Bitcoin is m/44'/0', Bitcoin Testnet is m/44'/1', and Litecoin is m/44'/2'.
The third level of the tree is "account," which allows users to subdivide their wallets into separate logical subaccounts, for accounting or organizational purposes. For example, an HD wallet might contain two bitcoin "accounts": m/44'/0'/0' and m/44'/0'/1'. Each account is the root of its own subtree.
On the fourth level, "change," an HD wallet has two subtrees, one for creating receiving addresses and one for creating change addresses. Note that whereas the previous levels used hardened derivation, this level uses normal derivation. This is to allow this level of the tree to export extended public keys for use in a nonsecured environment. Usable addresses are derived by the HD wallet as children of the fourth level, making the fifth level of the tree the "address_index." For example, the third receiving address for bitcoin payments in the primary account would be M/44'/0'/0'/0/2. [table_4-9] shows a few more examples.
| HD path | Key described |
|---|---|
M/44 |
The third receiving public key for the primary bitcoin account |
M/44 |
The fifteenth change-address public key for the fourth bitcoin account |
m/44 |
The second private key in the Litecoin main account, for signing transactions |
Transactions
Introduction
Transactions are the most important part of the bitcoin system. Everything else in bitcoin is designed to ensure that transactions can be created, propagated on the network, validated, and finally added to the global ledger of transactions (the blockchain). Transactions are data structures that encode the transfer of value between participants in the bitcoin system. Each transaction is a public entry in bitcoin’s blockchain, the global double-entry bookkeeping ledger.
In this chapter we will examine all the various forms of transactions, what they contain, how to create them, how they are verified, and how they become part of the permanent record of all transactions. When we use the term "wallet" in this chapter, we are referring to the software that constructs transactions, not just the database of keys.
Transactions in Detail
In [ch02_bitcoin_overview], we looked at the transaction Alice used to pay for coffee at Bob’s coffee shop using a block explorer ([alices_transactions_to_bobs_cafe]).
The block explorer application shows a transaction from Alice’s "address" to Bob’s "address." This is a much simplified view of what is contained in a transaction. In fact, as we will see in this chapter, much of the information shown is constructed by the block explorer and is not actually in the transaction.

Transactions—Behind the Scenes
Behind the scenes, an actual transaction looks very different from a transaction provided by a typical block explorer. In fact, most of the high-level constructs we see in the various bitcoin application user interfaces do not actually exist in the bitcoin system.
We can use Bitcoin Core’s command-line interface (getrawtransaction and decoderawtransaction) to retrieve Alice’s "raw" transaction, decode it, and see what it contains. The result looks like this:
{ "version": 1, "locktime": 0, "vin": [ { "txid": "7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18", "vout": 0, "scriptSig" : "3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL] 0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf", "sequence": 4294967295 } ], "vout": [ { "value": 0.01500000, "scriptPubKey": "OP_DUP OP_HASH160 ab68025513c3dbd2f7b92a94e0581f5d50f654e7 OP_EQUALVERIFY OP_CHECKSIG" }, { "value": 0.08450000, "scriptPubKey": "OP_DUP OP_HASH160 7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8 OP_EQUALVERIFY OP_CHECKSIG", } ] }
You may notice a few things about this transaction, mostly the things that are missing! Where is Alice’s address? Where is Bob’s address? Where is the 0.1 input "sent" by Alice? In bitcoin, there are no coins, no senders, no recipients, no balances, no accounts, and no addresses. All those things are constructed at a higher level for the benefit of the user, to make things easier to understand.
You may also notice a lot of strange and indecipherable fields and hexadecimal strings. Don’t worry, we will explain each field shown here in detail in this chapter.
Transaction Outputs and Inputs
The fundamental building block of a bitcoin transaction is a transaction output. Transaction outputs are indivisible chunks of bitcoin currency, recorded on the blockchain, and recognized as valid by the entire network. Bitcoin full nodes track all available and spendable outputs, known as unspent transaction outputs, or UTXO. The collection of all UTXO is known as the UTXO set and currently numbers in the millions of UTXO. The UTXO set grows as new UTXO is created and shrinks when UTXO is consumed. Every transaction represents a change (state transition) in the UTXO set.
When we say that a user’s wallet has "received" bitcoin, what we mean is that the wallet has detected a UTXO that can be spent with one of the keys controlled by that wallet. Thus, a user’s bitcoin "balance" is the sum of all UTXO that user’s wallet can spend and which may be scattered among hundreds of transactions and hundreds of blocks. The concept of a balance is created by the wallet application. The wallet calculates the user’s balance by scanning the blockchain and aggregating the value of any UTXO the wallet can spend with the keys it controls. Most wallets maintain a database or use a database service to store a quick reference set of all the UTXO they can spend with the keys they control.
A transaction output can have an arbitrary (integer) value denominated as a multiple of satoshis. Just like dollars can be divided down to two decimal places as cents, bitcoin can be divided down to eight decimal places as satoshis. Although an output can have any arbitrary value, once created it is indivisible. This is an important characteristic of outputs that needs to be emphasized: outputs are discrete and indivisible units of value, denominated in integer satoshis. An unspent output can only be consumed in its entirety by a transaction.
If an UTXO is larger than the desired value of a transaction, it must still be consumed in its entirety and change must be generated in the transaction. In other words, if you have a UTXO worth 20 bitcoin and want to pay only 1 bitcoin, your transaction must consume the entire 20-bitcoin UTXO and produce two outputs: one paying 1 bitcoin to your desired recipient and another paying 19 bitcoin in change back to your wallet. As a result of the indivisible nature of transaction outputs, most bitcoin transactions will have to generate change.
Imagine a shopper buying a $1.50 beverage, reaching into her wallet and trying to find a combination of coins and bank notes to cover the $1.50 cost. The shopper will choose exact change if available (e.g., a dollar bill and two quarters), or a combination of smaller denominations (six quarters), or if necessary, a larger unit such as a $5 note. If she hands too much money, say $5, to the shop owner, she will expect $3.50 change, which she will return to her wallet and have available for future transactions.
Similarly, a bitcoin transaction must be created from a user’s UTXO in whatever denominations that user has available. Users cannot cut an UTXO in half any more than they can cut a dollar bill in half and use it as currency. The user’s wallet application will typically select from the user’s available UTXO to compose an amount greater than or equal to the desired transaction amount.
As with real life, the bitcoin application can use several strategies to satisfy the purchase amount: combining several smaller units, finding exact change, or using a single unit larger than the transaction value and making change. All of this complex assembly of spendable UTXO is done by the user’s wallet automatically and is invisible to users. It is only relevant if you are programmatically constructing raw transactions from UTXO.
A transaction consumes previously recorded unspent transaction outputs and creates new transaction outputs that can be consumed by a future transaction. This way, chunks of bitcoin value move forward from owner to owner in a chain of transactions consuming and creating UTXO.
The exception to the output and input chain is a special type of transaction called the coinbase transaction, which is the first transaction in each block. This transaction is placed there by the "winning" miner and creates brand-new bitcoin payable to that miner as a reward for mining. This special coinbase transaction does not consume UTXO; instead, it has a special type of input called the "coinbase." This is how bitcoin’s money supply is created during the mining process, as we will see in [mining].
|
Tip
|
What comes first? Inputs or outputs, the chicken or the egg? Strictly speaking, outputs come first because coinbase transactions, which generate new bitcoin, have no inputs and create outputs from nothing. |
Transaction Outputs
Every bitcoin transaction creates outputs, which are recorded on the bitcoin ledger. Almost all of these outputs, with one exception (see [op_return]) create spendable chunks of bitcoin called UTXO, which are then recognized by the whole network and available for the owner to spend in a future transaction.
UTXO are tracked by every full-node bitcoin client in the UTXO set. New transactions consume (spend) one or more of these outputs from the UTXO set.
Transaction outputs consist of two parts:
-
An amount of bitcoin, denominated in satoshis, the smallest bitcoin unit
-
A cryptographic puzzle that determines the conditions required to spend the output
The cryptographic puzzle is also known as a locking script, a witness script, or a scriptPubKey.
The transaction scripting language, used in the locking script mentioned previously, is discussed in detail in [tx_script].
Now, let’s look at Alice’s transaction (shown previously in [transactions_behind_the_scenes]) and see if we can identify the outputs. In the JSON encoding, the outputs are in an array (list) named vout:
"vout": [ { "value": 0.01500000, "scriptPubKey": "OP_DUP OP_HASH160 ab68025513c3dbd2f7b92a94e0581f5d50f654e7 OP_EQUALVERIFY OP_CHECKSIG" }, { "value": 0.08450000, "scriptPubKey": "OP_DUP OP_HASH160 7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8 OP_EQUALVERIFY OP_CHECKSIG", } ]
As you can see, the transaction contains two outputs. Each output is defined by a value and a cryptographic puzzle. In the encoding shown by Bitcoin Core, the value is shown in bitcoin, but in the transaction itself it is recorded as an integer denominated in satoshis. The second part of each output is the cryptographic puzzle that sets the conditions for spending. Bitcoin Core shows this as scriptPubKey and shows us a human-readable representation of the script.
The topic of locking and unlocking UTXO will be discussed later, in [tx_lock_unlock]. The scripting language that is used for the script in scriptPubKey is discussed in [tx_script]. But before we delve into those topics, we need to understand the overall structure of transaction inputs and outputs.
Transaction serialization—outputs
When transactions are transmitted over the network or exchanged between applications, they are serialized. Serialization is the process of converting the internal representation of a data structure into a format that can be transmitted one byte at a time, also known as a byte stream. Serialization is most commonly used for encoding data structures for transmission over a network or for storage in a file. The serialization format of a transaction output is shown in [tx_out_structure].
| Size | Field | Description |
|---|---|---|
8 bytes (little-endian) |
Amount |
Bitcoin value in satoshis (10-8 bitcoin) |
1–9 bytes (VarInt) |
Locking-Script Size |
Locking-Script length in bytes, to follow |
Variable |
Locking-Script |
A script defining the conditions needed to spend the output |
Most bitcoin libraries and frameworks do not store transactions internally as byte-streams, as that would require complex parsing every time you needed to access a single field. For convenience and readability, bitcoin libraries store transactions internally in data structures (usually object-oriented structures).
The process of converting from the byte-stream representation of a transaction to a library’s internal representation data structure is called deserialization or transaction parsing. The process of converting back to a byte-stream for transmission over the network, for hashing, or for storage on disk is called serialization. Most bitcoin libraries have built-in functions for transaction serialization and deserialization.
See if you can manually decode Alice’s transaction from the serialized hexadecimal form, finding some of the elements we saw previously. The section containing the two outputs is highlighted in [example_6_1] to help you:
0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd73
4d2804fe65fa35779000000008b483045022100884d142d86652a3f47
ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039
ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813
01410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade84
16ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc1
7b4a10fa336a8d752adfffffffff0260e31600000000001976a914ab6
8025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef800000000000
1976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac
00000000
Here are some hints:
-
There are two outputs in the highlighted section, each serialized as shown in [tx_out_structure].
-
The value of 0.015 bitcoin is 1,500,000 satoshis. That’s
16 e3 60in hexadecimal. -
In the serialized transaction, the value
16 e3 60is encoded in little-endian (least-significant-byte-first) byte order, so it looks like60 e3 16. -
The
scriptPubKeylength is 25 bytes, which is19in hexadecimal.
Transaction Inputs
Transaction inputs identify (by reference) which UTXO will be consumed and provide proof of ownership through an unlocking script.
To build a transaction, a wallet selects from the UTXO it controls, UTXO with enough value to make the requested payment. Sometimes one UTXO is enough, other times more than one is needed. For each UTXO that will be consumed to make this payment, the wallet creates one input pointing to the UTXO and unlocks it with an unlocking script.
Let’s look at the components of an input in greater detail. The first part of an input is a pointer to an UTXO by reference to the transaction hash and sequence number where the UTXO is recorded in the blockchain. The second part is an unlocking script, which the wallet constructs in order to satisfy the spending conditions set in the UTXO. Most often, the unlocking script is a digital signature and public key proving ownership of the bitcoin. However, not all unlocking scripts contain signatures. The third part is a sequence number, which will be discussed later.
Consider our example in [transactions_behind_the_scenes]. The transaction inputs are an array (list) called vin:
"vin": [ { "txid": "7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18", "vout": 0, "scriptSig" : "3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL] 0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf", "sequence": 4294967295 } ]
As you can see, there is only one input in the list (because one UTXO contained sufficient value to make this payment). The input contains four elements:
-
A transaction ID, referencing the transaction that contains the UTXO being spent
-
An output index (
vout), identifying which UTXO from that transaction is referenced (first one is zero) -
A
scriptSig, which satisfies the conditions placed on the UTXO, unlocking it for spending -
A sequence number (to be discussed later)
In Alice’s transaction, the input points to the transaction ID:
7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18and output index 0 (i.e., the first UTXO created by that transaction). The unlocking script is constructed by Alice’s wallet by first retrieving the referenced UTXO, examining its locking script, and then using it to build the necessary unlocking script to satisfy it.
Looking just at the input you may have noticed that we don’t know anything about this UTXO, other than a reference to the transaction containing it. We don’t know its value (amount in satoshi), and we don’t know the locking script that sets the conditions for spending it. To find this information, we must retrieve the referenced UTXO by retrieving the underlying transaction. Notice that because the value of the input is not explicitly stated, we must also use the referenced UTXO in order to calculate the fees that will be paid in this transaction (see [tx_fees]).
It’s not just Alice’s wallet that needs to retrieve UTXO referenced in the inputs. Once this transaction is broadcast to the network, every validating node will also need to retrieve the UTXO referenced in the transaction inputs in order to validate the transaction.
Transactions on their own seem incomplete because they lack context. They reference UTXO in their inputs but without retrieving that UTXO we cannot know the value of the inputs or their locking conditions. When writing bitcoin software, anytime you decode a transaction with the intent of validating it or counting the fees or checking the unlocking script, your code will first have to retrieve the referenced UTXO from the blockchain in order to build the context implied but not present in the UTXO references of the inputs. For example, to calculate the amount paid in fees, you must know the sum of the values of inputs and outputs. But without retrieving the UTXO referenced in the inputs, you do not know their value. So a seemingly simple operation like counting fees in a single transaction in fact involves multiple steps and data from multiple transactions.
We can use the same sequence of commands with Bitcoin Core as we used when retrieving Alice’s transaction (getrawtransaction and decoderawtransaction). With that we can get the UTXO referenced in the preceding input and take a look:
"vout": [ { "value": 0.10000000, "scriptPubKey": "OP_DUP OP_HASH160 7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8 OP_EQUALVERIFY OP_CHECKSIG" } ]
We see that this UTXO has a value of 0.1 BTC and that it has a locking script (scriptPubKey) that contains "OP_DUP OP_HASH160…".
|
Tip
|
To fully understand Alice’s transaction we had to retrieve the previous transaction(s) referenced as inputs. A function that retrieves previous transactions and unspent transaction outputs is very common and exists in almost every bitcoin library and API. |
Transaction serialization—inputs
When transactions are serialized for transmission on the network, their inputs are encoded into a byte stream as shown in [tx_in_structure].
| Size | Field | Description |
|---|---|---|
32 bytes |
Transaction Hash |
Pointer to the transaction containing the UTXO to be spent |
4 bytes |
Output Index |
The index number of the UTXO to be spent; first one is 0 |
1–9 bytes (VarInt) |
Unlocking-Script Size |
Unlocking-Script length in bytes, to follow |
Variable |
Unlocking-Script |
A script that fulfills the conditions of the UTXO locking script |
4 bytes |
Sequence Number |
Used for locktime or disabled (0xFFFFFFFF) |
As with the outputs, let’s see if we can find the inputs from Alice’s transaction in the serialized format. First, the inputs decoded:
"vin": [ { "txid": "7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18", "vout": 0, "scriptSig" : "3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL] 0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf", "sequence": 4294967295 } ],
Now, let’s see if we can identify these fields in the serialized hex encoding in [example_6_2]:
0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd73
4d2804fe65fa35779000000008b483045022100884d142d86652a3f47
ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039
ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813
01410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade84
16ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc1
7b4a10fa336a8d752adfffffffff0260e31600000000001976a914ab6
8025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef800000000000
1976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac00000
000
Hints:
-
The transaction ID is serialized in reversed byte order, so it starts with (hex)
18and ends with79 -
The output index is a 4-byte group of zeros, easy to identify
-
The length of the
scriptSigis 139 bytes, or8bin hex -
The sequence number is set to
FFFFFFFF, again easy to identify
Transaction Fees
Most transactions include transaction fees, which compensate the bitcoin miners for securing the network. Fees also serve as a security mechanism themselves, by making it economically infeasible for attackers to flood the network with transactions. Mining and the fees and rewards collected by miners are discussed in more detail in [mining].
This section examines how transaction fees are included in a typical transaction. Most wallets calculate and include transaction fees automatically. However, if you are constructing transactions programmatically, or using a command-line interface, you must manually account for and include these fees.
Transaction fees serve as an incentive to include (mine) a transaction into the next block and also as a disincentive against abuse of the system by imposing a small cost on every transaction. Transaction fees are collected by the miner who mines the block that records the transaction on the blockchain.
Transaction fees are calculated based on the size of the transaction in kilobytes, not the value of the transaction in bitcoin. Overall, transaction fees are set based on market forces within the bitcoin network. Miners prioritize transactions based on many different criteria, including fees, and might even process transactions for free under certain circumstances. Transaction fees affect the processing priority, meaning that a transaction with sufficient fees is likely to be included in the next block mined, whereas a transaction with insufficient or no fees might be delayed, processed on a best-effort basis after a few blocks, or not processed at all. Transaction fees are not mandatory, and transactions without fees might be processed eventually; however, including transaction fees encourages priority processing.
Over time, the way transaction fees are calculated and the effect they have on transaction prioritization has evolved. At first, transaction fees were fixed and constant across the network. Gradually, the fee structure relaxed and may be influenced by market forces, based on network capacity and transaction volume. Since at least the beginning of 2016, capacity limits in bitcoin have created competition between transactions, resulting in higher fees and effectively making free transactions a thing of the past. Zero fee or very low fee transactions rarely get mined and sometimes will not even be propagated across the network.
In Bitcoin Core, fee relay policies are set by the minrelaytxfee option. The current default minrelaytxfee is 0.00001 bitcoin or a hundredth of a millibitcoin per kilobyte. Therefore, by default, transactions with a fee less than 0.0001 bitcoin are treated as free and are only relayed if there is space in the mempool; otherwise, they are dropped. Bitcoin nodes can override the default fee relay policy by adjusting the value of minrelaytxfee.
Any bitcoin service that creates transactions, including wallets, exchanges, retail applications, etc., must implement dynamic fees. Dynamic fees can be implemented through a third-party fee estimation service or with a built-in fee estimation algorithm. If you’re unsure, begin with a third-party service and as you gain experience design and implement your own algorithm if you wish to remove the third-party dependency.
Fee estimation algorithms calculate the appropriate fee, based on capacity and the fees offered by "competing" transactions. These algorithms range from simplistic (average or median fee in the last block) to sophisticated (statistical analysis). They estimate the necessary fee (in satoshis per byte) that will give a transaction a high probability of being selected and included within a certain number of blocks. Most services offer users the option of choosing high, medium, or low priority fees. High priority means users pay higher fees but the transaction is likely to be included in the next block. Medium and low priority means users pay lower transaction fees but the transactions may take much longer to confirm.
Many wallet applications use third-party services for fee calculations. One popular service is http://bitcoinfees.21.co, which provides an API and a visual chart showing the fee in satoshi/byte for different priorities.
|
Tip
|
Static fees are no longer viable on the bitcoin network. Wallets that set static fees will produce a poor user experience as transactions will often get "stuck" and remain unconfirmed. Users who don’t understand bitcoin transactions and fees are dismayed by "stuck" transactions because they think they’ve lost their money. |
The chart in [bitcoinfees21co] shows the real-time estimate of fees in 10 satoshi/byte increments and the expected confirmation time (in minutes and number of blocks) for transactions with fees in each range. For each fee range (e.g., 61–70 satoshi/byte), two horizontal bars show the number of unconfirmed transactions (1405) and total number of transactions in the past 24 hours (102,975), with fees in that range. Based on the graph, the recommended high-priority fee at this time was 80 satoshi/byte, a fee likely to result in the transaction being mined in the very next block (zero block delay). For perspective, the median transaction size is 226 bytes, so the recommended fee for a transaction size would be 18,080 satoshis (0.00018080 BTC).
The fee estimation data can be retrieved via a simple HTTP REST API, at https://bitcoinfees.21.co/api/v1/fees/recommended. For example, on the command line using the curl command:
$ curl https://bitcoinfees.21.co/api/v1/fees/recommended
{"fastestFee":80,"halfHourFee":80,"hourFee":60}The API returns a JSON object with the current fee estimate for fastest confirmation (fastestFee), confirmation within three blocks (halfHourFee) and six blocks (hourFee), in satoshi per byte.
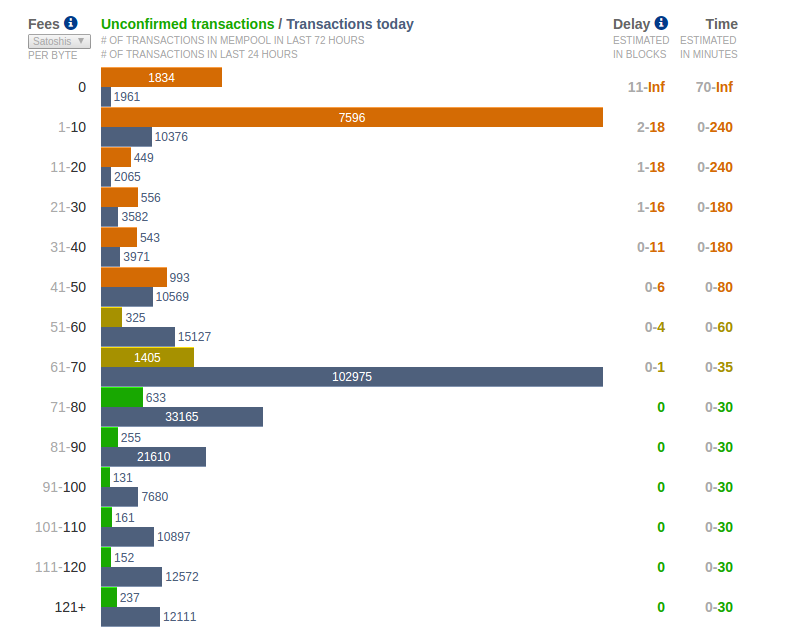
Adding Fees to Transactions
The data structure of transactions does not have a field for fees. Instead, fees are implied as the difference between the sum of inputs and the sum of outputs. Any excess amount that remains after all outputs have been deducted from all inputs is the fee that is collected by the miners:
Fees = Sum(Inputs) – Sum(Outputs)This is a somewhat confusing element of transactions and an important point to understand, because if you are constructing your own transactions you must ensure you do not inadvertently include a very large fee by underspending the inputs. That means that you must account for all inputs, if necessary by creating change, or you will end up giving the miners a very big tip!
For example, if you consume a 20-bitcoin UTXO to make a 1-bitcoin payment, you must include a 19-bitcoin change output back to your wallet. Otherwise, the 19-bitcoin "leftover" will be counted as a transaction fee and will be collected by the miner who mines your transaction in a block. Although you will receive priority processing and make a miner very happy, this is probably not what you intended.
|
Warning
|
If you forget to add a change output in a manually constructed transaction, you will be paying the change as a transaction fee. "Keep the change!" might not be what you intended. |
Let’s see how this works in practice, by looking at Alice’s coffee purchase again. Alice wants to spend 0.015 bitcoin to pay for coffee. To ensure this transaction is processed promptly, she will want to include a transaction fee, say 0.001. That will mean that the total cost of the transaction will be 0.016. Her wallet must therefore source a set of UTXO that adds up to 0.016 bitcoin or more and, if necessary, create change. Let’s say her wallet has a 0.2-bitcoin UTXO available. It will therefore need to consume this UTXO, create one output to Bob’s Cafe for 0.015, and a second output with 0.184 bitcoin in change back to her own wallet, leaving 0.001 bitcoin unallocated, as an implicit fee for the transaction.
Now let’s look at a different scenario. Eugenia, our children’s charity director in the Philippines, has completed a fundraiser to purchase schoolbooks for the children. She received several thousand small donations from people all around the world, totaling 50 bitcoin, so her wallet is full of very small payments (UTXO). Now she wants to purchase hundreds of schoolbooks from a local publisher, paying in bitcoin.
As Eugenia’s wallet application tries to construct a single larger payment transaction, it must source from the available UTXO set, which is composed of many smaller amounts. That means that the resulting transaction will source from more than a hundred small-value UTXO as inputs and only one output, paying the book publisher. A transaction with that many inputs will be larger than one kilobyte, perhaps a kilobyte or several kilobytes in size. As a result, it will require a much higher fee than the median-sized transaction.
Eugenia’s wallet application will calculate the appropriate fee by measuring the size of the transaction and multiplying that by the per-kilobyte fee. Many wallets will overpay fees for larger transactions to ensure the transaction is processed promptly. The higher fee is not because Eugenia is spending more money, but because her transaction is more complex and larger in size—the fee is independent of the transaction’s bitcoin value.
Transaction Scripts and Script Language
The bitcoin transaction script language, called Script, is a Forth-like reverse-polish notation stack-based execution language. If that sounds like gibberish, you probably haven’t studied 1960s programming languages, but that’s ok—we will explain it all in this chapter. Both the locking script placed on a UTXO and the unlocking script are written in this scripting language. When a transaction is validated, the unlocking script in each input is executed alongside the corresponding locking script to see if it satisfies the spending condition.
Script is a very simple language that was designed to be limited in scope and executable on a range of hardware, perhaps as simple as an embedded device. It requires minimal processing and cannot do many of the fancy things modern programming languages can do. For its use in validating programmable money, this is a deliberate security feature.
Today, most transactions processed through the bitcoin network have the form "Payment to Bob’s bitcoin address" and are based on a script called a Pay-to-Public-Key-Hash script. However, bitcoin transactions are not limited to the "Payment to Bob’s bitcoin address" script. In fact, locking scripts can be written to express a vast variety of complex conditions. In order to understand these more complex scripts, we must first understand the basics of transaction scripts and script language.
In this section, we will demonstrate the basic components of the bitcoin transaction scripting language and show how it can be used to express simple conditions for spending and how those conditions can be satisfied by unlocking scripts.
|
Tip
|
Bitcoin transaction validation is not based on a static pattern, but instead is achieved through the execution of a scripting language. This language allows for a nearly infinite variety of conditions to be expressed. This is how bitcoin gets the power of "programmable money." |
Turing Incompleteness
The bitcoin transaction script language contains many operators, but is deliberately limited in one important way—there are no loops or complex flow control capabilities other than conditional flow control. This ensures that the language is not Turing Complete, meaning that scripts have limited complexity and predictable execution times. Script is not a general-purpose language. These limitations ensure that the language cannot be used to create an infinite loop or other form of "logic bomb" that could be embedded in a transaction in a way that causes a denial-of-service attack against the bitcoin network. Remember, every transaction is validated by every full node on the bitcoin network. A limited language prevents the transaction validation mechanism from being used as a vulnerability.
Stateless Verification
The bitcoin transaction script language is stateless, in that there is no state prior to execution of the script, or state saved after execution of the script. Therefore, all the information needed to execute a script is contained within the script. A script will predictably execute the same way on any system. If your system verifies a script, you can be sure that every other system in the bitcoin network will also verify the script, meaning that a valid transaction is valid for everyone and everyone knows this. This predictability of outcomes is an essential benefit of the bitcoin system.
Script Construction (Lock + Unlock)
Bitcoin’s transaction validation engine relies on two types of scripts to validate transactions: a locking script and an unlocking script.
A locking script is a spending condition placed on an output: it specifies the conditions that must be met to spend the output in the future. Historically, the locking script was called a scriptPubKey, because it usually contained a public key or bitcoin address (public key hash). In this book we refer to it as a "locking script" to acknowledge the much broader range of possibilities of this scripting technology. In most bitcoin applications, what we refer to as a locking script will appear in the source code as scriptPubKey. You will also see the locking script referred to as a witness script (see [segwit]) or more generally as a cryptographic puzzle. These terms all mean the same thing, at different levels of abstraction.
An unlocking script is a script that "solves," or satisfies, the conditions placed on an output by a locking script and allows the output to be spent. Unlocking scripts are part of every transaction input. Most of the time they contain a digital signature produced by the user’s wallet from his or her private key. Historically, the unlocking script was called scriptSig, because it usually contained a digital signature. In most bitcoin applications, the source code refers to the unlocking script as scriptSig. You will also see the unlocking script referred to as a witness (see [segwit]). In this book, we refer to it as an "unlocking script" to acknowledge the much broader range of locking script requirements, because not all unlocking scripts must contain signatures.
Every bitcoin validating node will validate transactions by executing the locking and unlocking scripts together. Each input contains an unlocking script and refers to a previously existing UTXO. The validation software will copy the unlocking script, retrieve the UTXO referenced by the input, and copy the locking script from that UTXO. The unlocking and locking script are then executed in sequence. The input is valid if the unlocking script satisfies the locking script conditions (see [script_exec]). All the inputs are validated independently, as part of the overall validation of the transaction.
Note that the UTXO is permanently recorded in the blockchain, and therefore is invariable and is unaffected by failed attempts to spend it by reference in a new transaction. Only a valid transaction that correctly satisfies the conditions of the output results in the output being considered as "spent" and removed from the set of unspent transaction outputs (UTXO set).
[scriptSig_and_scriptPubKey] is an example of the unlocking and locking scripts for the most common type of bitcoin transaction (a payment to a public key hash), showing the combined script resulting from the concatenation of the unlocking and locking scripts prior to script validation.
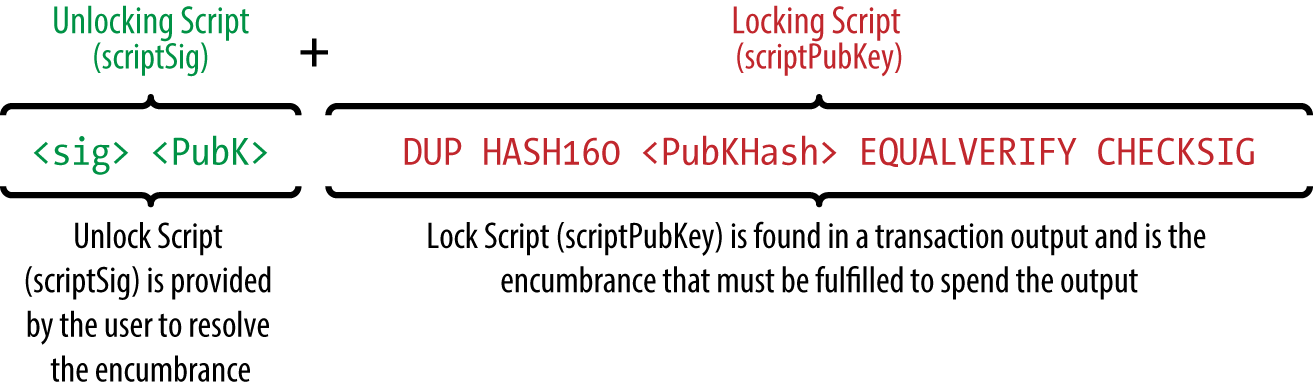
The script execution stack
Bitcoin’s scripting language is called a stack-based language because it uses a data structure called a stack. A stack is a very simple data structure that can be visualized as a stack of cards. A stack allows two operations: push and pop. Push adds an item on top of the stack. Pop removes the top item from the stack. Operations on a stack can only act on the topmost item on the stack. A stack data structure is also called a Last-In-First-Out, or "LIFO" queue.
The scripting language executes the script by processing each item from left to right. Numbers (data constants) are pushed onto the stack. Operators push or pop one or more parameters from the stack, act on them, and might push a result onto the stack. For example, OP_ADD will pop two items from the stack, add them, and push the resulting sum onto the stack.
Conditional operators evaluate a condition, producing a boolean result of TRUE or FALSE. For example, OP_EQUAL pops two items from the stack and pushes TRUE (TRUE is represented by the number 1) if they are equal or FALSE (represented by zero) if they are not equal. Bitcoin transaction scripts usually contain a conditional operator, so that they can produce the TRUE result that signifies a valid transaction.
A simple script
Now let’s apply what we’ve learned about scripts and stacks to some simple examples.
In [simplemath_script], the script 2 3 OP_ADD 5 OP_EQUAL demonstrates the arithmetic addition operator OP_ADD, adding two numbers and putting the result on the stack, followed by the conditional operator OP_EQUAL, which checks that the resulting sum is equal to 5. For brevity, the OP_ prefix is omitted in the step-by-step example. For more details on the available script operators and functions, see [tx_script_ops].
Although most locking scripts refer to a public key hash (essentially, a bitcoin address), thereby requiring proof of ownership to spend the funds, the script does not have to be that complex. Any combination of locking and unlocking scripts that results in a TRUE value is valid. The simple arithmetic we used as an example of the scripting language is also a valid locking script that can be used to lock a transaction output.
Use part of the arithmetic example script as the locking script:
3 OP_ADD 5 OP_EQUALwhich can be satisfied by a transaction containing an input with the unlocking script:
2The validation software combines the locking and unlocking scripts and the resulting script is:
2 3 OP_ADD 5 OP_EQUALAs we saw in the step-by-step example in [simplemath_script], when this script is executed, the result is OP_TRUE, making the transaction valid. Not only is this a valid transaction output locking script, but the resulting UTXO could be spent by anyone with the arithmetic skills to know that the number 2 satisfies the script.
|
Tip
|
Transactions are valid if the top result on the stack is |
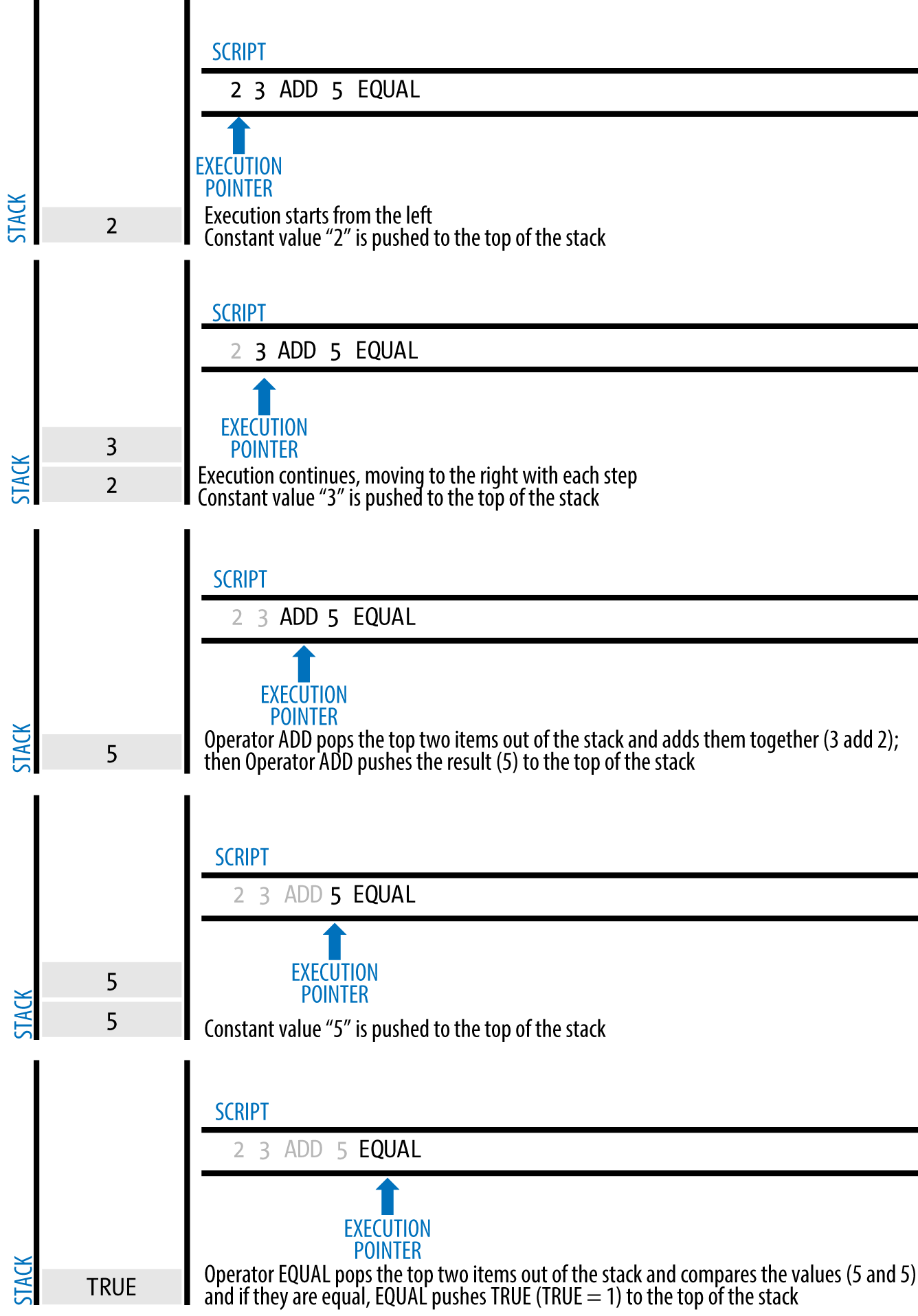
The following is a slightly more complex script, which calculates 2 + 7 — 3 + 1. Notice that when the script contains several operators in a row, the stack allows the results of one operator to be acted upon by the next operator:
2 7 OP_ADD 3 OP_SUB 1 OP_ADD 7 OP_EQUALTry validating the preceding script yourself using pencil and paper. When the script execution ends, you should be left with the value TRUE on the stack.
Separate execution of unlocking and locking scripts
In the original bitcoin client, the unlocking and locking scripts were concatenated and executed in sequence. For security reasons, this was changed in 2010, because of a vulnerability that allowed a malformed unlocking script to push data onto the stack and corrupt the locking script. In the current implementation, the scripts are executed separately with the stack transferred between the two executions, as described next.
First, the unlocking script is executed, using the stack execution engine. If the unlocking script is executed without errors (e.g., it has no "dangling" operators left over), the main stack (not the alternate stack) is copied and the locking script is executed. If the result of executing the locking script with the stack data copied from the unlocking script is "TRUE," the unlocking script has succeeded in resolving the conditions imposed by the locking script and, therefore, the input is a valid authorization to spend the UTXO. If any result other than "TRUE" remains after execution of the combined script, the input is invalid because it has failed to satisfy the spending conditions placed on the UTXO.
Pay-to-Public-Key-Hash (P2PKH)
The vast majority of transactions processed on the bitcoin network spend outputs locked with a Pay-to-Public-Key-Hash or "P2PKH" script. These outputs contain a locking script that locks the output to a public key hash, more commonly known as a bitcoin address. An output locked by a P2PKH script can be unlocked (spent) by presenting a public key and a digital signature created by the corresponding private key (see [digital_sigs]).
For example, let’s look at Alice’s payment to Bob’s Cafe again. Alice made a payment of 0.015 bitcoin to the cafe’s bitcoin address. That transaction output would have a locking script of the form:
OP_DUP OP_HASH160 <Cafe Public Key Hash> OP_EQUALVERIFY OP_CHECKSIGThe Cafe Public Key Hash is equivalent to the bitcoin address of the cafe, without the Base58Check encoding. Most applications would show the public key hash in hexadecimal encoding and not the familiar bitcoin address Base58Check format that begins with a "1."
The preceding locking script can be satisfied with an unlocking script of the form:
<Cafe Signature> <Cafe Public Key>The two scripts together would form the following combined validation script:
<Cafe Signature> <Cafe Public Key> OP_DUP OP_HASH160
<Cafe Public Key Hash> OP_EQUALVERIFY OP_CHECKSIGWhen executed, this combined script will evaluate to TRUE if, and only if, the unlocking script matches the conditions set by the locking script. In other words, the result will be TRUE if the unlocking script has a valid signature from the cafe’s private key that corresponds to the public key hash set as an encumbrance.
Figures #P2PubKHash1 and #P2PubKHash2 show (in two parts) a step-by-step execution of the combined script, which will prove this is a valid transaction.
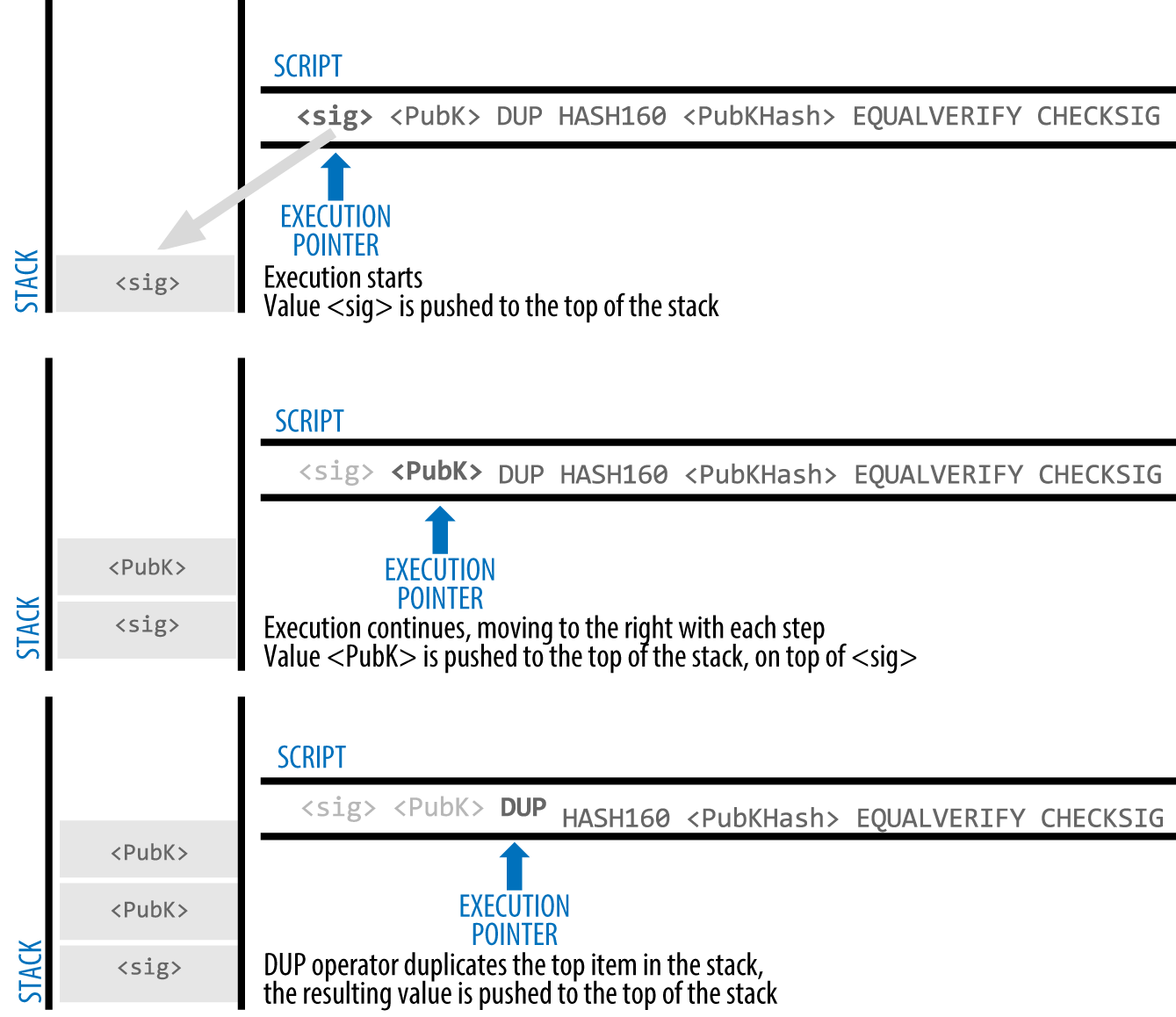
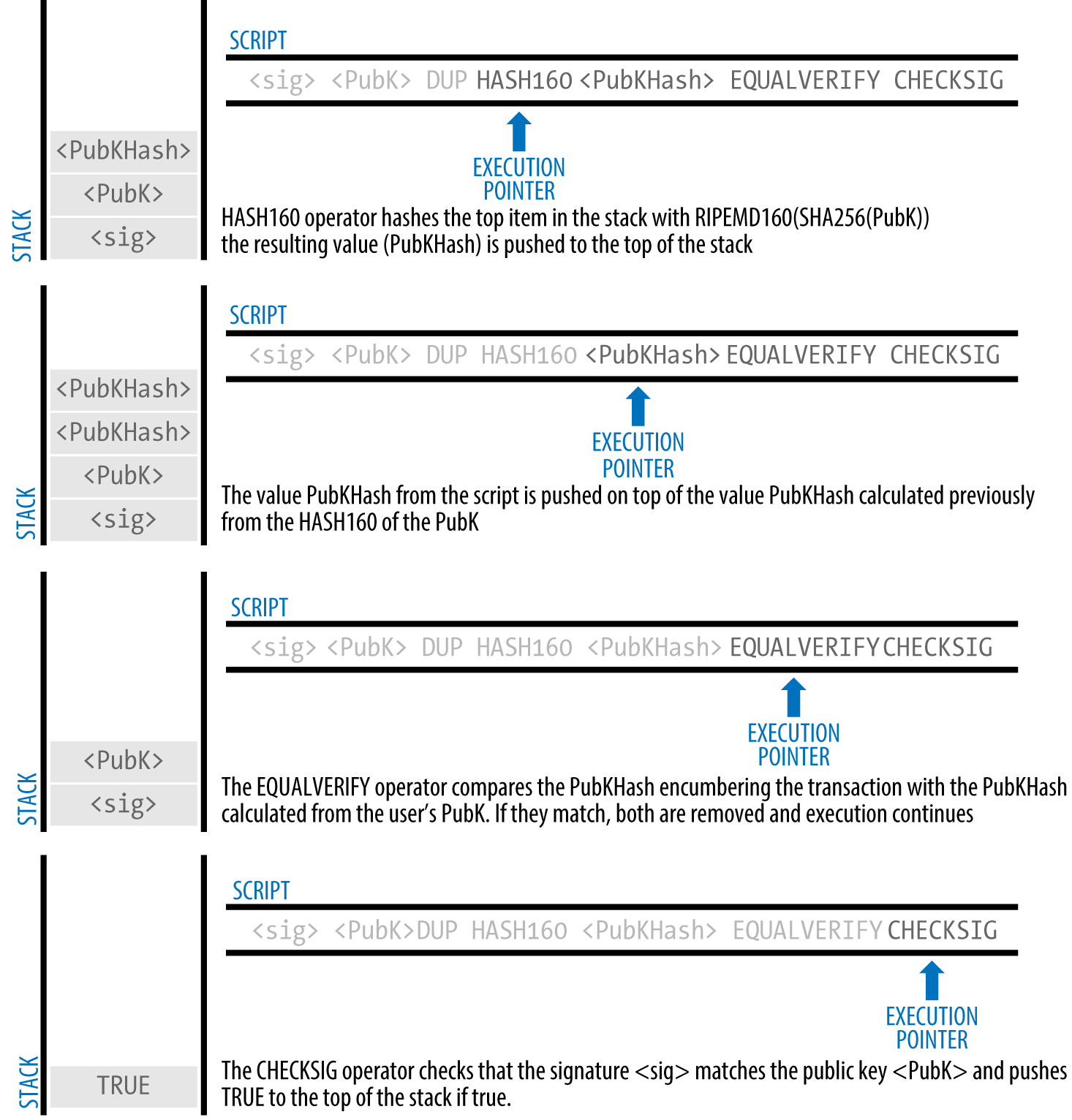
Digital Signatures (ECDSA)
So far, we have not delved into any detail about "digital signatures." In this section we look at how digital signatures work and how they can present proof of ownership of a private key without revealing that private key.
The digital signature algorithm used in bitcoin is the Elliptic Curve Digital Signature Algorithm, or ECDSA. ECDSA is the algorithm used for digital signatures based on elliptic curve private/public key pairs, as described in [elliptic_curve]. ECDSA is used by the script functions OP_CHECKSIG, OP_CHECKSIGVERIFY, OP_CHECKMULTISIG, and OP_CHECKMULTISIGVERIFY. Any time you see those in a locking script, the unlocking script must contain an ECDSA signature.
A digital signature serves three purposes in bitcoin (see the following sidebar). First, the signature proves that the owner of the private key, who is by implication the owner of the funds, has authorized the spending of those funds. Secondly, the proof of authorization is undeniable (nonrepudiation). Thirdly, the signature proves that the transaction (or specific parts of the transaction) have not and cannot be modified by anyone after it has been been signed.
Note that each transaction input is signed independently. This is critical, as neither the signatures nor the inputs have to belong to or be applied by the same "owners." In fact, a specific transaction scheme called "CoinJoin" uses this fact to create multi-party transactions for privacy.
|
Note
|
Each transaction input and any signature it may contain is completely independent of any other input or signature. Multiple parties can collaborate to construct transactions and sign only one input each. |
How Digital Signatures Work
A digital signature is a mathematical scheme that consists of two parts. The first part is an algorithm for creating a signature, using a private key (the signing key), from a message (the transaction). The second part is an algorithm that allows anyone to verify the signature, given also the message and a public key.
Creating a digital signature
In bitcoin’s implementation of the ECDSA algorithm, the "message" being signed is the transaction, or more accurately a hash of a specific subset of the data in the transaction (see [sighash_types]). The signing key is the user’s private key. The result is the signature:
\(Sig = F_{sig}(F_{hash}(m), dA)\)
where:
-
dA is the signing private key
-
m is the transaction (or parts of it)
-
Fhash is the hashing function
-
Fsig is the signing algorithm
-
Sig is the resulting signature
More details on the mathematics of ECDSA can be found in [ecdsa_math].
The function Fsig produces a signature Sig that is composed of two values, commonly referred to as R and S:
Sig = (R, S)Now that the two values R and S have been calculated, they are serialized into a byte-stream using an international standard encoding scheme called the Distinguished Encoding Rules, or DER.
Serialization of signatures (DER)
Let’s look at the transaction Alice created again. In the transaction input there is an unlocking script that contains the following DER-encoded signature from Alice’s wallet:
3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e381301That signature is a serialized byte-stream of the R and S values produced by Alice’s wallet to prove she owns the private key authorized to spend that output. The serialization format consists of nine elements as follows:
-
0x30—indicating the start of a DER sequence -
0x45—the length of the sequence (69 bytes) -
0x02—an integer value follows -
0x21—the length of the integer (33 bytes) -
R—00884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb -
0x02—another integer follows -
0x20—the length of the integer (32 bytes) -
S—4b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813 -
A suffix (
0x01) indicating the type of hash used (SIGHASH_ALL)
See if you can decode Alice’s serialized (DER-encoded) signature using this list. The important numbers are R and S; the rest of the data is part of the DER encoding scheme.
Verifying the Signature
To verify the signature, one must have the signature (R and S), the serialized transaction, and the public key (that corresponds to the private key used to create the signature). Essentially, verification of a signature means "Only the owner of the private key that generated this public key could have produced this signature on this transaction."
The signature verification algorithm takes the message (a hash of the transaction or parts of it), the signer’s public key and the signature (R and S values), and returns TRUE if the signature is valid for this message and public key.
Signature Hash Types (SIGHASH)
Digital signatures are applied to messages, which in the case of bitcoin, are the transactions themselves. The signature implies a commitment by the signer to specific transaction data. In the simplest form, the signature applies to the entire transaction, thereby committing all the inputs, outputs, and other transaction fields. However, a signature can commit to only a subset of the data in a transaction, which is useful for a number of scenarios as we will see in this section.
Bitcoin signatures have a way of indicating which part of a transaction’s data is included in the hash signed by the private key using a SIGHASH flag. The SIGHASH flag is a single byte that is appended to the signature. Every signature has a SIGHASH flag and the flag can be different from to input to input. A transaction with three signed inputs may have three signatures with different SIGHASH flags, each signature signing (committing) different parts of the transaction.
Remember, each input may contain a signature in its unlocking script. As a result, a transaction that contains several inputs may have signatures with different SIGHASH flags that commit different parts of the transaction in each of the inputs. Note also that bitcoin transactions may contain inputs from different "owners," who may sign only one input in a partially constructed (and invalid) transaction, collaborating with others to gather all the necessary signatures to make a valid transaction. Many of the SIGHASH flag types only make sense if you think of multiple participants collaborating outside the bitcoin network and updating a partially signed transaction.
There are three SIGHASH flags: ALL, NONE, and SINGLE, as shown in [sighash_types_and_their].
SIGHASH flag |
Value | Description |
|---|---|---|
|
0x01 |
Signature applies to all inputs and outputs |
|
0x02 |
Signature applies to all inputs, none of the outputs |
|
0x03 |
Signature applies to all inputs but only the one output with the same index number as the signed input |
In addition, there is a modifier flag SIGHASH_ANYONECANPAY, which can be combined with each of the preceding flags. When ANYONECANPAY is set, only one input is signed, leaving the rest (and their sequence numbers) open for modification. The ANYONECANPAY has the value 0x80 and is applied by bitwise OR, resulting in the combined flags as shown in [sighash_types_with_modifiers].
| SIGHASH flag | Value | Description |
|---|---|---|
ALL|ANYONECANPAY |
0x81 |
Signature applies to one inputs and all outputs |
NONE|ANYONECANPAY |
0x82 |
Signature applies to one inputs, none of the outputs |
SINGLE|ANYONECANPAY |
0x83 |
Signature applies to one input and the output with the same index number |
The way SIGHASH flags are applied during signing and verification is that a copy of the transaction is made and certain fields within are truncated (set to zero length and emptied). The resulting transaction is serialized. The SIGHASH flag is added to the end of the serialized transaction and the result is hashed. The hash itself is the "message" that is signed. Depending on which SIGHASH flag is used, different parts of the transaction are truncated. The resulting hash depends on different subsets of the data in the transaction. By including the SIGHASH as the last step before hashing, the signature commits the SIGHASH type as well, so it can’t be changed (e.g., by a miner).
|
Note
|
All |
In the example of Alice’s transaction (see the list in [seralization_of_signatures_der]), we saw that the last part of the DER-encoded signature was 01, which is the SIGHASH_ALL flag. This locks the transaction data, so Alice’s signature is committing the state of all inputs and outputs. This is the most common signature form.
Let’s look at some of the other SIGHASH types and how they can be used in practice:
-
ALL|ANYONECANPAY -
This construction can be used to make a "crowdfunding”-style transaction. Someone attempting to raise funds can construct a transaction with a single output. The single output pays the "goal" amount to the fundraiser. Such a transaction is obviously not valid, as it has no inputs. However, others can now amend it by adding an input of their own, as a donation. They sign their own input with
ALL|ANYONECANPAY. Unless enough inputs are gathered to reach the value of the output, the transaction is invalid. Each donation is a "pledge," which cannot be collected by the fundraiser until the entire goal amount is raised. -
NONE -
This construction can be used to create a "bearer check" or "blank check" of a specific amount. It commits to the input, but allows the output locking script to be changed. Anyone can write their own bitcoin address into the output locking script and redeem the transaction. However, the output value itself is locked by the signature.
-
NONE|ANYONECANPAY -
This construction can be used to build a "dust collector." Users who have tiny UTXO in their wallets can’t spend these without the cost in fees exceeding the value of the dust. With this type of signature, the dust UTXO can be donated for anyone to aggregate and spend whenever they want.
There are some proposals to modify or expand the SIGHASH system. One such proposal is Bitmask Sighash Modes by Blockstream’s Glenn Willen, as part of the Elements project. This aims to create a flexible replacement for SIGHASH types that allows "arbitrary, miner-rewritable bitmasks of inputs and outputs" that can express "more complex contractual precommitment schemes, such as signed offers with change in a distributed asset exchange."
|
Note
|
You will not see |
ECDSA Math
As mentioned previously, signatures are created by a mathematical function Fsig that produces a signature composed of two values R and S. In this section we look at the function Fsig in more detail.
The signature algorithm first generates an ephemeral (temporary) private public key pair. This temporary key pair is used in the calculation of the R and S values, after a transformation involving the signing private key and the transaction hash.
The temporary key pair is based on a random number k, which is used as the temporary private key. From k, we generate the corresponding temporary public key P (calculated as P = k*G, in the same way bitcoin public keys are derived; see [pubkey]). The R value of the digital signature is then the x coordinate of the ephemeral public key P.
From there, the algorithm calculates the S value of the signature, such that:
S = k-1 (Hash(m) + dA * R) mod p
where:
-
k is the ephemeral private key
-
R is the x coordinate of the ephemeral public key
-
dA is the signing private key
-
m is the transaction data
-
p is the prime order of the elliptic curve
Verification is the inverse of the signature generation function, using the R, S values and the public key to calculate a value P, which is a point on the elliptic curve (the ephemeral public key used in signature creation):
P = S-1 * Hash(m) * G + S-1 * R * Qa
where:
-
R and S are the signature values
-
Qa is Alice’s public key
-
m is the transaction data that was signed
-
G is the elliptic curve generator point
If the x coordinate of the calculated point P is equal to R, then the verifier can conclude that the signature is valid.
Note that in verifying the signature, the private key is neither known nor revealed.
|
Tip
|
The math of ECDSA is complex and difficult to understand. There are a number of great guides online that might help. Search for "ECDSA explained" or try this one: http://bit.ly/2r0HhGB. |
The Importance of Randomness in Signatures
As we saw in [ecdsa_math], the signature generation algorithm uses a random key k, as the basis for an ephemeral private/public key pair. The value of k is not important, as long as it is random. If the same value k is used to produce two signatures on different messages (transactions), then the signing private key can be calculated by anyone. Reuse of the same value for k in a signature algorithm leads to exposure of the private key!
|
Warning
|
If the same value k is used in the signing algorithm on two different transactions, the private key can be calculated and exposed to the world! |
This is not just a theoretical possibility. We have seen this issue lead to exposure of private keys in a few different implementations of transaction-signing algorithms in bitcoin. People have had funds stolen because of inadvertent reuse of a k value. The most common reason for reuse of a k value is an improperly initialized random-number generator.
To avoid this vulnerability, the industry best practice is to not generate k with a random-number generator seeded with entropy, but instead to use a deterministic-random process seeded with the transaction data itself. This ensures that each transaction produces a different k. The industry-standard algorithm for deterministic initialization of k is defined in RFC 6979, published by the Internet Engineering Task Force.
If you are implementing an algorithm to sign transactions in bitcoin, you must use RFC 6979 or a similarly deterministic-random algorithm to ensure you generate a different k for each transaction.
Bitcoin Addresses, Balances, and Other Abstractions
We began this chapter with the discovery that transactions look very different "behind the scenes" than how they are presented in wallets, blockchain explorers, and other user-facing applications. Many of the simplistic and familiar concepts from the earlier chapters, such as bitcoin addresses and balances, seem to be absent from the transaction structure. We saw that transactions don’t contain bitcoin addresses, per se, but instead operate through scripts that lock and unlock discrete values of bitcoin. Balances are not present anywhere in this system and yet every wallet application prominently displays the balance of the user’s wallet.
Now that we have explored what is actually included in a bitcoin transaction, we can examine how the higher-level abstractions are derived from the seemingly primitive components of the transaction.
Let’s look again at how Alice’s transaction was presented on a popular block explorer ([alice_transaction_to_bobs_cafe]).

On the left side of the transaction, the blockchain explorer shows Alice’s bitcoin address as the "sender." In fact, this information is not in the transaction itself. When the blockchain explorer retrieved the transaction it also retrieved the previous transaction referenced in the input and extracted the first output from that older transaction. Within that output is a locking script that locks the UTXO to Alice’s public key hash (a P2PKH script). The blockchain explorer extracted the public key hash and encoded it using Base58Check encoding to produce and display the bitcoin address that represents that public key.
Similarly, on the right side, the blockchain explorer shows the two outputs; the first to Bob’s bitcoin address and the second to Alice’s bitcoin address (as change). Once again, to create these bitcoin addresses, the blockchain explorer extracted the locking script from each output, recognized it as a P2PKH script, and extracted the public-key-hash from within. Finally, the blockchain explorer reencoded that public key hash with Base58Check to produce and display the bitcoin addresses.
If you were to click on Bob’s bitcoin address, the blockchain explorer would show you the view in [the_balance_of_bobs_bitcoin_address].
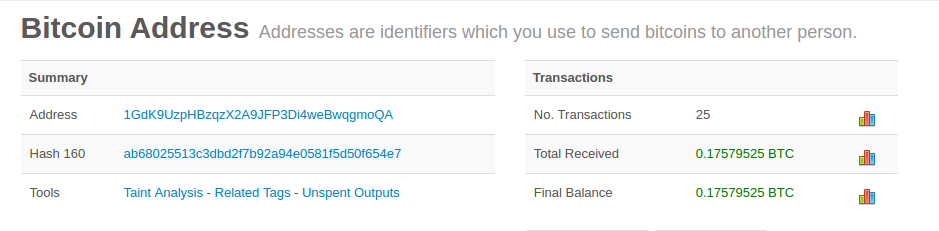
The blockchain explorer displays the balance of Bob’s bitcoin address. But nowhere in the bitcoin system is there a concept of a "balance." Rather, the values displayed here are constructed by the blockchain explorer as follows.
To construct the "Total Received" amount, the blockchain explorer first will decode the Base58Check encoding of the bitcoin address to retrieve the 160-bit hash of Bob’s public key that is encoded within the address. Then, the blockchain explorer will search through the database of transactions, looking for outputs with P2PKH locking scripts that contain Bob’s public key hash. By summing up the value of all the outputs, the blockchain explorer can produce the total value received.
Constructing the current balance (displayed as "Final Balance") requires a bit more work. The blockchain explorer keeps a separate database of the outputs that are currently unspent, the UTXO set. To maintain this database, the blockchain explorer must monitor the bitcoin network, add newly created UTXO, and remove spent UTXO, in real time, as they appear in unconfirmed transactions. This is a complicated process that depends on keeping track of transactions as they propagate, as well as maintaining consensus with the bitcoin network to ensure that the correct chain is followed. Sometimes, the blockchain explorer goes out of sync and its perspective of the UTXO set is incomplete or incorrect.
From the UTXO set, the blockchain explorer sums up the value of all unspent outputs referencing Bob’s public key hash and produces the "Final Balance" number shown to the user.
In order to produce this one image, with these two "balances," the blockchain explorer has to index and search through dozens, hundreds, or even hundreds of thousands of transactions.
In summary, the information presented to users through wallet applications, blockchain explorers, and other bitcoin user interfaces is often composed of higher-level abstractions that are derived by searching many different transactions, inspecting their content, and manipulating the data contained within them. By presenting this simplistic view of bitcoin transactions that resemble bank checks from one sender to one recipient, these applications have to abstract a lot of underlying detail. They mostly focus on the common types of transactions: P2PKH with SIGHASH_ALL signatures on every input. Thus, while bitcoin applications can present more than 80% of all transactions in an easy-to-read manner, they are sometimes stumped by transactions that deviate from the norm. Transactions that contain more complex locking scripts, or different SIGHASH flags, or many inputs and outputs, demonstrate the simplicity and weakness of these abstractions.
Every day, hundreds of transactions that do not contain P2PKH outputs are confirmed on the blockchain. The blockchain explorers often present these with red warning messages saying they cannot decode an address. The following link contains the most recent "strange transactions" that were not fully decoded: https://blockchain.info/strange-transactions.
As we will see in the next chapter, these are not necessarily strange transactions. They are transactions that contain more complex locking scripts than the common P2PKH. We will learn how to decode and understand more complex scripts and the applications they support next.
Advanced Transactions and Scripting
Introduction
In the previous chapter, we introduced the basic elements of bitcoin transactions and looked at the most common type of transaction script, the P2PKH script. In this chapter we will look at more advanced scripting and how we can use it to build transactions with complex conditions.
First, we will look at multisignature scripts. Next, we will examine the second most common transaction script, Pay-to-Script-Hash, which opens up a whole world of complex scripts. Then, we will examine new script operators that add a time dimension to bitcoin, through timelocks.
Multisignature
Multisignature scripts set a condition where N public keys are recorded in the script and at least M of those must provide signatures to unlock the funds. This is also known as an M-of-N scheme, where N is the total number of keys and M is the threshold of signatures required for validation. For example, a 2-of-3 multisignature is one where three public keys are listed as potential signers and at least two of those must be used to create signatures for a valid transaction to spend the funds. At this time, standard multisignature scripts are limited to at most 15 listed public keys, meaning you can do anything from a 1-of-1 to a 15-of-15 multisignature or any combination within that range. The limitation to 15 listed keys might be lifted by the time this book is published, so check the isStandard() function to see what is currently accepted by the network.
The general form of a locking script setting an M-of-N multisignature condition is:
M <Public Key 1> <Public Key 2> ... <Public Key N> N CHECKMULTISIGwhere N is the total number of listed public keys and M is the threshold of required signatures to spend the output.
A locking script setting a 2-of-3 multisignature condition looks like this:
2 <Public Key A> <Public Key B> <Public Key C> 3 CHECKMULTISIGThe preceding locking script can be satisfied with an unlocking script containing pairs of signatures and public keys:
<Signature B> <Signature C>or any combination of two signatures from the private keys corresponding to the three listed public keys.
The two scripts together would form the combined validation script:
<Signature B> <Signature C> 2 <Public Key A> <Public Key B> <Public Key C> 3 CHECKMULTISIGWhen executed, this combined script will evaluate to TRUE if, and only if, the unlocking script matches the conditions set by the locking script. In this case, the condition is whether the unlocking script has a valid signature from the two private keys that correspond to two of the three public keys set as an encumbrance.
A bug in CHECKMULTISIG execution
There is a bug in CHECKMULTISIG's execution that requires a slight workaround. When CHECKMULTISIG executes, it should consume M+N+2 items on the stack as parameters. However, due to the bug, CHECKMULTISIG will pop an extra value or one value more than expected.
Let’s look at this in greater detail using the previous validation example:
<Signature B> <Signature C> 2 <Public Key A> <Public Key B> <Public Key C> 3 CHECKMULTISIGFirst, CHECKMULTISIG pops the top item, which is N (in this example "3"). Then it pops N items, which are the public keys that can sign. In this example, public keys A, B, and C. Then, it pops one item, which is M, the quorum (how many signatures are needed). Here M = 2. At this point, CHECKMULTISIG should pop the final M items, which are the signatures, and see if they are valid. However, unfortunately, a bug in the implementation causes CHECKMULTISIG to pop one more item (M+1 total) than it should. The extra item is disregarded when checking the signatures so it has no direct effect on CHECKMULTISIG itself. However, an extra value must be present because if it is not present, when CHECKMULTISIG attempts to pop on an empty stack, it will cause a stack error and script failure (marking the transaction as invalid). Because the extra item is disregarded it can be anything, but customarily 0 is used.
Because this bug became part of the consensus rules, it must now be replicated forever. Therefore the correct script validation would look like this:
0 <Signature B> <Signature C> 2 <Public Key A> <Public Key B> <Public Key C> 3 CHECKMULTISIGThus the unlocking script actually used in multisig is not:
<Signature B> <Signature C>but instead it is:
0 <Signature B> <Signature C>From now on, if you see a multisig unlocking script, you should expect to see an extra 0 in the beginning, whose only purpose is as a workaround to a bug that accidentally became a consensus rule.
Pay-to-Script-Hash (P2SH)
Pay-to-Script-Hash (P2SH) was introduced in 2012 as a powerful new type of transaction that greatly simplifies the use of complex transaction scripts. To explain the need for P2SH, let’s look at a practical example.
In [ch01_intro_what_is_bitcoin] we introduced Mohammed, an electronics importer based in Dubai. Mohammed’s company uses bitcoin’s multisignature feature extensively for its corporate accounts. Multisignature scripts are one of the most common uses of bitcoin’s advanced scripting capabilities and are a very powerful feature. Mohammed’s company uses a multisignature script for all customer payments, known in accounting terms as "accounts receivable," or AR. With the multisignature scheme, any payments made by customers are locked in such a way that they require at least two signatures to release, from Mohammed and one of his partners or from his attorney who has a backup key. A multisignature scheme like that offers corporate governance controls and protects against theft, embezzlement, or loss.
The resulting script is quite long and looks like this:
2 <Mohammed's Public Key> <Partner1 Public Key> <Partner2 Public Key> <Partner3 Public Key> <Attorney Public Key> 5 CHECKMULTISIGAlthough multisignature scripts are a powerful feature, they are cumbersome to use. Given the preceding script, Mohammed would have to communicate this script to every customer prior to payment. Each customer would have to use special bitcoin wallet software with the ability to create custom transaction scripts, and each customer would have to understand how to create a transaction using custom scripts. Furthermore, the resulting transaction would be about five times larger than a simple payment transaction, because this script contains very long public keys. The burden of that extra-large transaction would be borne by the customer in the form of fees. Finally, a large transaction script like this would be carried in the UTXO set in RAM in every full node, until it was spent. All of these issues make using complex locking scripts difficult in practice.
P2SH was developed to resolve these practical difficulties and to make the use of complex scripts as easy as a payment to a bitcoin address. With P2SH payments, the complex locking script is replaced with its digital fingerprint, a cryptographic hash. When a transaction attempting to spend the UTXO is presented later, it must contain the script that matches the hash, in addition to the unlocking script. In simple terms, P2SH means "pay to a script matching this hash, a script that will be presented later when this output is spent."
In P2SH transactions, the locking script that is replaced by a hash is referred to as the redeem script because it is presented to the system at redemption time rather than as a locking script. [without_p2sh] shows the script without P2SH and [with_p2sh] shows the same script encoded with P2SH.
Locking Script |
2 PubKey1 PubKey2 PubKey3 PubKey4 PubKey5 5 CHECKMULTISIG |
Unlocking Script |
Sig1 Sig2 |
Redeem Script |
2 PubKey1 PubKey2 PubKey3 PubKey4 PubKey5 5 CHECKMULTISIG |
Locking Script |
HASH160 <20-byte hash of redeem script> EQUAL |
Unlocking Script |
Sig1 Sig2 <redeem script> |
As you can see from the tables, with P2SH the complex script that details the conditions for spending the output (redeem script) is not presented in the locking script. Instead, only a hash of it is in the locking script and the redeem script itself is presented later, as part of the unlocking script when the output is spent. This shifts the burden in fees and complexity from the sender to the recipient (spender) of the transaction.
Let’s look at Mohammed’s company, the complex multisignature script, and the resulting P2SH scripts.
First, the multisignature script that Mohammed’s company uses for all incoming payments from customers:
2 <Mohammed's Public Key> <Partner1 Public Key> <Partner2 Public Key> <Partner3 Public Key> <Attorney Public Key> 5 CHECKMULTISIGIf the placeholders are replaced by actual public keys (shown here as 520-bit numbers starting with 04) you can see that this script becomes very long:
2
04C16B8698A9ABF84250A7C3EA7EEDEF9897D1C8C6ADF47F06CF73370D74DCCA01CDCA79DCC5C395D7EEC6984D83F1F50C900A24DD47F569FD4193AF5DE762C58704A2192968D8655D6A935BEAF2CA23E3FB87A3495E7AF308EDF08DAC3C1FCBFC2C75B4B0F4D0B1B70CD2423657738C0C2B1D5CE65C97D78D0E34224858008E8B49047E63248B75DB7379BE9CDA8CE5751D16485F431E46117B9D0C1837C9D5737812F393DA7D4420D7E1A9162F0279CFC10F1E8E8F3020DECDBC3C0DD389D99779650421D65CBD7149B255382ED7F78E946580657EE6FDA162A187543A9D85BAAA93A4AB3A8F044DADA618D087227440645ABE8A35DA8C5B73997AD343BE5C2AFD94A5043752580AFA1ECED3C68D446BCAB69AC0BA7DF50D56231BE0AABF1FDEEC78A6A45E394BA29A1EDF518C022DD618DA774D207D137AAB59E0B000EB7ED238F4D800 5 CHECKMULTISIGThis entire script can instead be represented by a 20-byte cryptographic hash, by first applying the SHA256 hashing algorithm and then applying the RIPEMD160 algorithm on the result. The 20-byte hash of the preceding script is:
54c557e07dde5bb6cb791c7a540e0a4796f5e97eA P2SH transaction locks the output to this hash instead of the longer script, using the locking script:
HASH160 54c557e07dde5bb6cb791c7a540e0a4796f5e97e EQUALwhich, as you can see, is much shorter. Instead of "pay to this 5-key multisignature script," the P2SH equivalent transaction is "pay to a script with this hash." A customer making a payment to Mohammed’s company need only include this much shorter locking script in his payment. When Mohammed and his partners want to spend this UTXO, they must present the original redeem script (the one whose hash locked the UTXO) and the signatures necessary to unlock it, like this:
<Sig1> <Sig2> <2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIG>The two scripts are combined in two stages. First, the redeem script is checked against the locking script to make sure the hash matches:
<2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIG> HASH160 <redeem scriptHash> EQUALIf the redeem script hash matches, the unlocking script is executed on its own, to unlock the redeem script:
<Sig1> <Sig2> 2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIGAlmost all the scripts described in this chapter can only be implemented as P2SH scripts. They cannot be used directly in the locking script of a UTXO.
P2SH Addresses
Another important part of the P2SH feature is the ability to encode a script hash as an address, as defined in BIP-13. P2SH addresses are Base58Check encodings of the 20-byte hash of a script, just like bitcoin addresses are Base58Check encodings of the 20-byte hash of a public key. P2SH addresses use the version prefix "5," which results in Base58Check-encoded addresses that start with a "3." For example, Mohammed’s complex script, hashed and Base58Check-encoded as a P2SH address, becomes 39RF6JqABiHdYHkfChV6USGMe6Nsr66Gzw. Now, Mohammed can give this "address" to his customers and they can use almost any bitcoin wallet to make a simple payment, as if it were a bitcoin address. The 3 prefix gives them a hint that this is a special type of address, one corresponding to a script instead of a public key, but otherwise it works in exactly the same way as a payment to a bitcoin address.
P2SH addresses hide all of the complexity, so that the person making a payment does not see the script.
Benefits of P2SH
The P2SH feature offers the following benefits compared to the direct use of complex scripts in locking outputs:
-
Complex scripts are replaced by shorter fingerprints in the transaction output, making the transaction smaller.
-
Scripts can be coded as an address, so the sender and the sender’s wallet don’t need complex engineering to implement P2SH.
-
P2SH shifts the burden of constructing the script to the recipient, not the sender.
-
P2SH shifts the burden in data storage for the long script from the output (which is in the UTXO set) to the input (stored on the blockchain).
-
P2SH shifts the burden in data storage for the long script from the present time (payment) to a future time (when it is spent).
-
P2SH shifts the transaction fee cost of a long script from the sender to the recipient, who has to include the long redeem script to spend it.
Redeem Script and Validation
Prior to version 0.9.2 of the Bitcoin Core client, Pay-to-Script-Hash was limited to the standard types of bitcoin transaction scripts, by the isStandard() function. That means that the redeem script presented in the spending transaction could only be one of the standard types: P2PK, P2PKH, or multisig nature, excluding RETURN and P2SH itself.
As of version 0.9.2 of the Bitcoin Core client, P2SH transactions can contain any valid script, making the P2SH standard much more flexible and allowing for experimentation with many novel and complex types of transactions.
Note that you are not able to put a P2SH inside a P2SH redeem script, because the P2SH specification is not recursive. While it is technically possible to include RETURN in a redeem script, as nothing in the rules prevents you from doing so, it is of no practical use because executing RETURN during validation will cause the transaction to be marked invalid.
Note that because the redeem script is not presented to the network until you attempt to spend a P2SH output, if you lock an output with the hash of an invalid redeem script it will be processed regardless. The UTXO will be successfully locked. However, you will not be able to spend it because the spending transaction, which includes the redeem script, will not be accepted because it is an invalid script. This creates a risk, because you can lock bitcoin in a P2SH that cannot be spent later. The network will accept the P2SH locking script even if it corresponds to an invalid redeem script, because the script hash gives no indication of the script it represents.
|
Warning
|
P2SH locking scripts contain the hash of a redeem script, which gives no clues as to the content of the redeem script itself. The P2SH transaction will be considered valid and accepted even if the redeem script is invalid. You might accidentally lock bitcoin in such a way that it cannot later be spent. |
Data Recording Output (RETURN)
Bitcoin’s distributed and timestamped ledger, the blockchain, has potential uses far beyond payments. Many developers have tried to use the transaction scripting language to take advantage of the security and resilience of the system for applications such as digital notary services, stock certificates, and smart contracts. Early attempts to use bitcoin’s script language for these purposes involved creating transaction outputs that recorded data on the blockchain; for example, to record a digital fingerprint of a file in such a way that anyone could establish proof-of-existence of that file on a specific date by reference to that transaction.
The use of bitcoin’s blockchain to store data unrelated to bitcoin payments is a controversial subject. Many developers consider such use abusive and want to discourage it. Others view it as a demonstration of the powerful capabilities of blockchain technology and want to encourage such experimentation. Those who object to the inclusion of nonpayment data argue that it causes "blockchain bloat," burdening those running full bitcoin nodes with carrying the cost of disk storage for data that the blockchain was not intended to carry. Moreover, such transactions create UTXO that cannot be spent, using the destination bitcoin address as a freeform 20-byte field. Because the address is used for data, it doesn’t correspond to a private key and the resulting UTXO can never be spent; it’s a fake payment. These transactions that can never be spent are therefore never removed from the UTXO set and cause the size of the UTXO database to forever increase, or "bloat."
In version 0.9 of the Bitcoin Core client, a compromise was reached with the introduction of the RETURN operator. RETURN allows developers to add 80 bytes of nonpayment data to a transaction output. However, unlike the use of "fake" UTXO, the RETURN operator creates an explicitly provably unspendable output, which does not need to be stored in the UTXO set. RETURN outputs are recorded on the blockchain, so they consume disk space and contribute to the increase in the blockchain’s size, but they are not stored in the UTXO set and therefore do not bloat the UTXO memory pool and burden full nodes with the cost of more expensive RAM.
RETURN scripts look like this:
RETURN <data>The data portion is limited to 80 bytes and most often represents a hash, such as the output from the SHA256 algorithm (32 bytes). Many applications put a prefix in front of the data to help identify the application. For example, the Proof of Existence digital notarization service uses the 8-byte prefix DOCPROOF, which is ASCII encoded as 44 4f 43 50 52 4f 4f 46 in hexadecimal.
Keep in mind that there is no "unlocking script" that corresponds to RETURN that could possibly be used to "spend" a RETURN output. The whole point of RETURN is that you can’t spend the money locked in that output, and therefore it does not need to be held in the UTXO set as potentially spendable—RETURN is provably unspendable. RETURN is usually an output with a zero bitcoin amount, because any bitcoin assigned to such an output is effectively lost forever. If a RETURN is referenced as an input in a transaction, the script validation engine will halt the execution of the validation script and mark the transaction as invalid. The execution of RETURN essentially causes the script to "RETURN" with a FALSE and halt. Thus, if you accidentally reference a RETURN output as an input in a transaction, that transaction is invalid.
A standard transaction (one that conforms to the isStandard() checks) can have only one RETURN output. However, a single RETURN output can be combined in a transaction with outputs of any other type.
Two new command-line options have been added in Bitcoin Core as of version 0.10. The option datacarrier controls relay and mining of RETURN transactions, with the default set to "1" to allow them. The option datacarriersize takes a numeric argument specifying the maximum size in bytes of the RETURN script, 83 bytes by default, which, allows for a maximum of 80 bytes of RETURN data plus one byte of RETURN opcode and two bytes of PUSHDATA opcode.
|
Note
|
|
Timelocks
Timelocks are restrictions on transactions or outputs that only allow spending after a point in time. Bitcoin has had a transaction-level timelock feature from the beginning. It is implemented by the nLocktime field in a transaction. Two new timelock features were introduced in late 2015 and mid-2016 that offer UTXO-level timelocks. These are CHECKLOCKTIMEVERIFY and CHECKSEQUENCEVERIFY.
Timelocks are useful for postdating transactions and locking funds to a date in the future. More importantly, timelocks extend bitcoin scripting into the dimension of time, opening the door for complex multistep smart contracts.
Transaction Locktime (nLocktime)
From the beginning, bitcoin has had a transaction-level timelock feature. Transaction locktime is a transaction-level setting (a field in the transaction data structure) that defines the earliest time that a transaction is valid and can be relayed on the network or added to the blockchain. Locktime is also known as nLocktime from the variable name used in the Bitcoin Core codebase. It is set to zero in most transactions to indicate immediate propagation and execution. If nLocktime is nonzero and below 500 million, it is interpreted as a block height, meaning the transaction is not valid and is not relayed or included in the blockchain prior to the specified block height. If it is above 500 million, it is interpreted as a Unix Epoch timestamp (seconds since Jan-1-1970) and the transaction is not valid prior to the specified time. Transactions with nLocktime specifying a future block or time must be held by the originating system and transmitted to the bitcoin network only after they become valid. If a transaction is transmitted to the network before the specified nLocktime, the transaction will be rejected by the first node as invalid and will not be relayed to other nodes. The use of nLocktime is equivalent to postdating a paper check.
Transaction locktime limitations
nLocktime has the limitation that while it makes it possible to spend some outputs in the future, it does not make it impossible to spend them until that time. Let’s explain that with the following example.
Alice signs a transaction spending one of her outputs to Bob’s address, and sets the transaction nLocktime to 3 months in the future. Alice sends that transaction to Bob to hold. With this transaction Alice and Bob know that:
-
Bob cannot transmit the transaction to redeem the funds until 3 months have elapsed.
-
Bob may transmit the transaction after 3 months.
However:
-
Alice can create another transaction, double-spending the same inputs without a locktime. Thus, Alice can spend the same UTXO before the 3 months have elapsed.
-
Bob has no guarantee that Alice won’t do that.
It is important to understand the limitations of transaction nLocktime. The only guarantee is that Bob will not be able to redeem it before 3 months have elapsed. There is no guarantee that Bob will get the funds. To achieve such a guarantee, the timelock restriction must be placed on the UTXO itself and be part of the locking script, rather than on the transaction. This is achieved by the next form of timelock, called Check Lock Time Verify.
Check Lock Time Verify (CLTV)
In December 2015, a new form of timelock was introduced to bitcoin as a soft fork upgrade. Based on a specifications in BIP-65, a new script operator called CHECKLOCKTIMEVERIFY (CLTV) was added to the scripting language. CLTV is a per-output timelock, rather than a per-transaction timelock as is the case with nLocktime. This allows for much greater flexibility in the way timelocks are applied.
In simple terms, by adding the CLTV opcode in the redeem script of an output it restricts the output, so that it can only be spent after the specified time has elapsed.
|
Tip
|
While |
CLTV doesn’t replace nLocktime, but rather restricts specific UTXO such that they can only be spent in a future transaction with nLocktime set to a greater or equal value.
The CLTV opcode takes one parameter as input, expressed as a number in the same format as nLocktime (either a block height or Unix epoch time). As indicated by the VERIFY suffix, CLTV is the type of opcode that halts execution of the script if the outcome is FALSE. If it results in TRUE, execution continues.
In order to lock an output with CLTV, you insert it into the redeem script of the output in the transaction that creates the output. For example, if Alice is paying Bob’s address, the output would normally contain a P2PKH script like this:
DUP HASH160 <Bob's Public Key Hash> EQUALVERIFY CHECKSIGTo lock it to a time, say 3 months from now, the transaction would be a P2SH transaction with a redeem script like this:
<now + 3 months> CHECKLOCKTIMEVERIFY DROP DUP HASH160 <Bob's Public Key Hash> EQUALVERIFY CHECKSIGwhere <now + 3 months> is a block height or time value estimated 3 months from the time the transaction is mined: current block height + 12,960 (blocks) or current Unix epoch time + 7,760,000 (seconds). For now, don’t worry about the DROP opcode that follows CHECKLOCKTIMEVERIFY; it will be explained shortly.
When Bob tries to spend this UTXO, he constructs a transaction that references the UTXO as an input. He uses his signature and public key in the unlocking script of that input and sets the transaction nLocktime to be equal or greater to the timelock in the CHECKLOCKTIMEVERIFY Alice set. Bob then broadcasts the transaction on the bitcoin network.
Bob’s transaction is evaluated as follows. If the CHECKLOCKTIMEVERIFY parameter Alice set is less than or equal the spending transaction’s nLocktime, script execution continues (acts as if a “no operation” or NOP opcode was executed). Otherwise, script execution halts and the transaction is deemed invalid.
More precisely, CHECKLOCKTIMEVERIFY fails and halts execution, marking the transaction invalid if (source: BIP-65):
-
the stack is empty; or
-
the top item on the stack is less than 0; or
-
the lock-time type (height versus timestamp) of the top stack item and the
nLocktimefield are not the same; or -
the top stack item is greater than the transaction’s
nLocktimefield; or -
the
nSequencefield of the input is 0xffffffff.
|
Note
|
|
After execution, if CLTV is satisfied, the time parameter that preceded it remains as the top item on the stack and may need to be dropped, with DROP, for correct execution of subsequent script opcodes. You will often see CHECKLOCKTIMEVERIFY followed by DROP in scripts for this reason.
By using nLocktime in conjunction with CLTV, the scenario described in [locktime_limitations] changes. Because Alice locked the UTXO itself, it is now impossible for either Bob or Alice to spend it before the 3-month locktime has expired.
By introducing timelock functionality directly into the scripting language, CLTV allows us to develop some very interesting complex scripts.
The standard is defined in BIP-65 (CHECKLOCKTIMEVERIFY).
Relative Timelocks
nLocktime and CLTV are both absolute timelocks in that they specify an absolute point in time. The next two timelock features we will examine are relative timelocks in that they specify, as a condition of spending an output, an elapsed time from the confirmation of the output in the blockchain.
Relative timelocks are useful because they allow a chain of two or more interdependent transactions to be held off chain, while imposing a time constraint on one transaction that is dependent on the elapsed time from the confirmation of a previous transaction. In other words, the clock doesn’t start counting until the UTXO is recorded on the blockchain. This functionality is especially useful in bidirectional state channels and Lightning Networks, as we will see in [state_channels].
Relative timelocks, like absolute timelocks, are implemented with both a transaction-level feature and a script-level opcode. The transaction-level relative timelock is implemented as a consensus rule on the value of nSequence, a transaction field that is set in every transaction input. Script-level relative timelocks are implemented with the CHECKSEQUENCEVERIFY (CSV) opcode.
Relative timelocks are implemented according to the specifications in BIP-68, Relative lock-time using consensus-enforced sequence numbers and BIP-112, CHECKSEQUENCEVERIFY.
BIP-68 and BIP-112 were activated in May 2016 as a soft fork upgrade to the consensus rules.
Relative Timelocks with nSequence
Relative timelocks can be set on each input of a transaction, by setting the nSequence field in each input.
Original meaning of nSequence
The nSequence field was originally intended (but never properly implemented) to allow modification of transactions in the mempool. In that use, a transaction containing inputs with nSequence value below 232 (0xFFFFFFFF) indicated a transaction that was not yet "finalized." Such a transaction would be held in the mempool until it was replaced by another transaction spending the same inputs with a higher nSequence value. Once a transaction was received whose inputs had an nSequence value of 232 it would be considered "finalized" and mined.
The original meaning of nSequence was never properly implemented and the value of nSequence is customarily set to 232 in transactions that do not utilize timelocks. For transactions with nLocktime or CHECKLOCKTIMEVERIFY, the nSequence value must be set to less than 232 for the timelock guards to have effect. Customarily, it is set to 232 – 1 (0xFFFFFFFE).
nSequence as a consensus-enforced relative timelock
Since the activation of BIP-68, new consensus rules apply for any transaction containing an input whose nSequence value is less than 231 (bit 1<<31 is not set). Programmatically, that means that if the most significant (bit 1<<31) is not set, it is a flag that means "relative locktime." Otherwise (bit 1<<31 set), the nSequence value is reserved for other uses such as enabling CHECKLOCKTIMEVERIFY, nLocktime, Opt-In-Replace-By-Fee, and other future developments.
Transaction inputs with nSequence values less than 231 are interpreted as having a relative timelock. Such a transaction is only valid once the input has aged by the relative timelock amount. For example, a transaction with one input with an nSequence relative timelock of 30 blocks is only valid when at least 30 blocks have elapsed from the time the UTXO referenced in the input was mined. Since nSequence is a per-input field, a transaction may contain any number of timelocked inputs, all of which must have sufficiently aged for the transaction to be valid. A transaction can include both timelocked inputs (nSequence < 231) and inputs without a relative timelock (nSequence >= 231).
The nSequence value is specified in either blocks or seconds, but in a slightly different format than we saw used in nLocktime. A type-flag is used to differentiate between values counting blocks and values counting time in seconds. The type-flag is set in the 23rd least-significant bit (i.e., value 1<<22). If the type-flag is set, then the nSequence value is interpreted as a multiple of 512 seconds. If the type-flag is not set, the nSequence value is interpreted as a number of blocks.
When interpreting nSequence as a relative timelock, only the 16 least significant bits are considered. Once the flags (bits 32 and 23) are evaluated, the nSequence value is usually "masked" with a 16-bit mask (e.g., nSequence & 0x0000FFFF).
[bip_68_def_of_nseq] shows the binary layout of the nSequence value, as defined by BIP-68.
Relative timelocks based on consensus enforcement of the nSequence value are defined in BIP-68.
The standard is defined in BIP-68, Relative lock-time using consensus-enforced sequence numbers.
Relative Timelocks with CSV
Just like CLTV and nLocktime, there is a script opcode for relative timelocks that leverages the nSequence value in scripts. That opcode is CHECKSEQUENCEVERIFY, commonly referred to as CSV for short.
The CSV opcode when evaluated in a UTXO’s redeem script allows spending only in a transaction whose input nSequence value is greater than or equal to the CSV parameter. Essentially, this restricts spending the UTXO until a certain number of blocks or seconds have elapsed relative to the time the UTXO was mined.
As with CLTV, the value in CSV must match the format in the corresponding nSequence value. If CSV is specified in terms of blocks, then so must nSequence. If CSV is specified in terms of seconds, then so must nSequence.
Relative timelocks with CSV are especially useful when several (chained) transactions are created and signed, but not propagated, when they’re kept "off-chain." A child transaction cannot be used until the parent transaction has been propagated, mined, and aged by the time specified in the relative timelock. One application of this use case can be seen in [state_channels] and [lightning_network].
CSV is defined in detail in BIP-112, CHECKSEQUENCEVERIFY.
Median-Time-Past
As part of the activation of relative timelocks, there was also a change in the way "time" is calculated for timelocks (both absolute and relative). In bitcoin there is a subtle, but very significant, difference between wall time and consensus time. Bitcoin is a decentralized network, which means that each participant has his or her own perspective of time. Events on the network do not occur instantaneously everywhere. Network latency must be factored into the perspective of each node. Eventually everything is synchronized to create a common ledger. Bitcoin reaches consensus every 10 minutes about the state of the ledger as it existed in the past.
The timestamps set in block headers are set by the miners. There is a certain degree of latitude allowed by the consensus rules to account for differences in clock accuracy between decentralized nodes. However, this creates an unfortunate incentive for miners to lie about the time in a block so as to earn extra fees by including timelocked transactions that are not yet mature. See the following section for more information.
To remove the incentive to lie and strengthen the security of timelocks, a BIP was proposed and activated at the same time as the BIPs for relative timelocks. This is BIP-113, which defines a new consensus measurement of time called Median-Time-Past.
Median-Time-Past is calculated by taking the timestamps of the last 11 blocks and finding the median. That median time then becomes consensus time and is used for all timelock calculations. By taking the midpoint from approximately two hours in the past, the influence of any one block’s timestamp is reduced. By incorporating 11 blocks, no single miner can influence the timestamps in order to gain fees from transactions with a timelock that hasn’t yet matured.
Median-Time-Past changes the implementation of time calculations for nLocktime, CLTV, nSequence, and CSV. The consensus time calculated by Median-Time-Past is always approximately one hour behind wall clock time. If you create timelock transactions, you should account for it when estimating the desired value to encode in nLocktime, nSequence, CLTV, and CSV.
Median-Time-Past is specified in BIP-113.
Timelock Defense Against Fee Sniping
Fee-sniping is a theoretical attack scenario, where miners attempting to rewrite past blocks "snipe" higher-fee transactions from future blocks to maximize their profitability.
For example, let’s say the highest block in existence is block #100,000. If instead of attempting to mine block #100,001 to extend the chain, some miners attempt to remine #100,000. These miners can choose to include any valid transaction (that hasn’t been mined yet) in their candidate block #100,000. They don’t have to remine the block with the same transactions. In fact, they have the incentive to select the most profitable (highest fee per kB) transactions to include in their block. They can include any transactions that were in the "old" block #100,000, as well as any transactions from the current mempool. Essentially they have the option to pull transactions from the "present" into the rewritten "past" when they re-create block #100,000.
Today, this attack is not very lucrative, because block reward is much higher than total fees per block. But at some point in the future, transaction fees will be the majority of the reward (or even the entirety of the reward). At that time, this scenario becomes inevitable.
To prevent "fee sniping," when Bitcoin Core creates transactions, it uses nLocktime to limit them to the "next block," by default. In our scenario, Bitcoin Core would set nLocktime to 100,001 on any transaction it created. Under normal circumstances, this nLocktime has no effect—the transactions could only be included in block #100,001 anyway; it’s the next block.
But under a blockchain fork attack, the miners would not be able to pull high-fee transactions from the mempool, because all those transactions would be timelocked to block #100,001. They can only remine #100,000 with whatever transactions were valid at that time, essentially gaining no new fees.
To achieve this, Bitcoin Core sets the nLocktime on all new transactions to <current block # + 1> and sets the nSequence on all the inputs to 0xFFFFFFFE to enable nLocktime.
Scripts with Flow Control (Conditional Clauses)
One of the more powerful features of Bitcoin Script is flow control, also known as conditional clauses. You are probably familiar with flow control in various programming languages that use the construct IF…THEN…ELSE. Bitcoin conditional clauses look a bit different, but are essentially the same construct.
At a basic level, bitcoin conditional opcodes allow us to construct a redeem script that has two ways of being unlocked, depending on a TRUE/FALSE outcome of evaluating a logical condition. For example, if x is TRUE, the redeem script is A and the ELSE redeem script is B.
Additionally, bitcoin conditional expressions can be "nested" indefinitely, meaning that a conditional clause can contain another within it, which contains another, etc. Bitcoin Script flow control can be used to construct very complex scripts with hundreds or even thousands of possible execution paths. There is no limit to nesting, but consensus rules impose a limit on the maximum size, in bytes, of a script.
Bitcoin implements flow control using the IF, ELSE, ENDIF, and NOTIF opcodes. Additionally, conditional expressions can contain boolean operators such as BOOLAND, BOOLOR, and NOT.
At first glance, you may find the bitcoin’s flow control scripts confusing. That is because Bitcoin Script is a stack language. The same way that 1 + 1 looks "backward" when expressed as 1 1 ADD, flow control clauses in bitcoin also look "backward."
In most traditional (procedural) programming languages, flow control looks like this:
if (condition):
code to run when condition is true
else:
code to run when condition is false
code to run in either caseIn a stack-based language like Bitcoin Script, the logical condition comes before the IF, which makes it look "backward," like this:
condition
IF
code to run when condition is true
ELSE
code to run when condition is false
ENDIF
code to run in either caseWhen reading Bitcoin Script, remember that the condition being evaluated comes before the IF opcode.
Conditional Clauses with VERIFY Opcodes
Another form of conditional in Bitcoin Script is any opcode that ends in VERIFY. The VERIFY suffix means that if the condition evaluated is not TRUE, execution of the script terminates immediately and the transaction is deemed invalid.
Unlike an IF clause, which offers alternative execution paths, the VERIFY suffix acts as a guard clause, continuing only if a precondition is met.
For example, the following script requires Bob’s signature and a pre-image (secret) that produces a specific hash. Both conditions must be satisfied to unlock:
EQUALVERIFY guard clause.HASH160 <expected hash> EQUALVERIFY <Bob's Pubkey> CHECKSIGTo redeem this, Bob must construct an unlocking script that presents a valid pre-image and a signature:
<Bob's Sig> <hash pre-image>Without presenting the pre-image, Bob can’t get to the part of the script that checks for his signature.
This script can be written with an IF instead:
IF guard clauseHASH160 <expected hash> EQUAL
IF
<Bob's Pubkey> CHECKSIG
ENDIFBob’s unlocking script is identical:
<Bob's Sig> <hash pre-image>The script with IF does the same thing as using an opcode with a VERIFY suffix; they both operate as guard clauses. However, the VERIFY construction is more efficient, using one fewer opcode.
So, when do we use VERIFY and when do we use IF? If all we are trying to do is to attach a precondition (guard clause), then VERIFY is better. If, however, we want to have more than one execution path (flow control), then we need an IF…ELSE flow control clause.
|
Tip
|
An opcode such as |
Using Flow Control in Scripts
A very common use for flow control in Bitcoin Script is to construct a redeem script that offers multiple execution paths, each a different way of redeeming the UTXO.
Let’s look at a simple example, where we have two signers, Alice and Bob, and either one is able to redeem. With multisig, this would be expressed as a 1-of-2 multisig script. For the sake of demonstration, we will do the same thing with an IF clause:
IF
<Alice's Pubkey> CHECKSIG
ELSE
<Bob's Pubkey> CHECKSIG
ENDIFLooking at this redeem script, you may be wondering: "Where is the condition? There is nothing preceding the IF clause!"
The condition is not part of the redeem script. Instead, the condition will be offered in the unlocking script, allowing Alice and Bob to "choose" which execution path they want.
Alice redeems this with the unlocking script:
<Alice's Sig> 1The 1 at the end serves as the condition (TRUE) that will make the IF clause execute the first redemption path for which Alice has a signature.
For Bob to redeem this, he would have to choose the second execution path by giving a FALSE value to the IF clause:
<Bob's Sig> 0Bob’s unlocking script puts a 0 on the stack, causing the IF clause to execute the second (ELSE) script, which requires Bob’s signature.
Since IF clauses can be nested, we can create a "maze" of execution paths. The unlocking script can provide a "map" selecting which execution path is actually executed:
IF
script A
ELSE
IF
script B
ELSE
script C
ENDIF
ENDIFIn this scenario, there are three execution paths (script A, script B, and script C). The unlocking script provides a path in the form of a sequence of TRUE or FALSE values. To select path script B, for example, the unlocking script must end in 1 0 (TRUE, FALSE). These values will be pushed onto the stack, so that the second value (FALSE) ends up at the top of the stack. The outer IF clause pops the FALSE value and executes the first ELSE clause. Then the TRUE value moves to the top of the stack and is evaluated by the inner (nested) IF, selecting the B execution path.
Using this construct, we can build redeem scripts with tens or hundreds of execution paths, each offering a different way to redeem the UTXO. To spend, we construct an unlocking script that navigates the execution path by putting the appropriate TRUE and FALSE values on the stack at each flow control point.
Complex Script Example
In this section we combine many of the concepts from this chapter into a single example.
Our example uses the story of Mohammed, the company owner in Dubai who is operating an import/export business.
In this example, Mohammed wishes to construct a company capital account with flexible rules. The scheme he creates requires different levels of authorization depending on timelocks. The participants in the multisig scheme are Mohammed, his two partners Saeed and Zaira, and their company lawyer Abdul. The three partners make decisions based on a majority rule, so two of the three must agree. However, in the case of a problem with their keys, they want their lawyer to be able to recover the funds with one of the three partner signatures. Finally, if all partners are unavailable or incapacitated for a while, they want the lawyer to be able to manage the account directly.
Here’s the script that Mohammed designs to achieve this:
IF
IF
2
ELSE
<30 days> CHECKSEQUENCEVERIFY DROP
<Abdul the Lawyer's Pubkey> CHECKSIGVERIFY
1
ENDIF
<Mohammed's Pubkey> <Saeed's Pubkey> <Zaira's Pubkey> 3 CHECKMULTISIG
ELSE
<90 days> CHECKSEQUENCEVERIFY DROP
<Abdul the Lawyer's Pubkey> CHECKSIG
ENDIFMohammed’s script implements three execution paths using nested IF…ELSE flow control clauses.
In the first execution path, this script operates as a simple 2-of-3 multisig with the three partners. This execution path consists of lines 3 and 9. Line 3 sets the quorum of the multisig to 2 (2-of-3). This execution path can be selected by putting TRUE TRUE at the end of the unlocking script:
0 <Mohammed's Sig> <Zaira's Sig> TRUE TRUE|
Tip
|
The |
The second execution path can only be used after 30 days have elapsed from the creation of the UTXO. At that time, it requires the signature of Abdul the lawyer and one of the three partners (a 1-of-3 multisig). This is achieved by line 7, which sets the quorum for the multisig to 1. To select this execution path, the unlocking script would end in FALSE TRUE:
0 <Saeed's Sig> <Abdul's Sig> FALSE TRUE|
Tip
|
Why |
Finally, the third execution path allows Abdul the lawyer to spend the funds alone, but only after 90 days. To select this execution path, the unlocking script has to end in FALSE:
<Abdul's Sig> FALSETry running the script on paper to see how it behaves on the stack.
A few more things to consider when reading this example. See if you can find the answers:
-
Why can’t the lawyer redeem the third execution path at any time by selecting it with
FALSEon the unlocking script? -
How many execution paths can be used 5, 35, and 105 days, respectively, after the UTXO is mined?
-
Are the funds lost if the lawyer loses his key? Does your answer change if 91 days have elapsed?
-
How do the partners "reset" the clock every 29 or 89 days to prevent the lawyer from accessing the funds?
-
Why do some
CHECKSIGopcodes in this script have theVERIFYsuffix while others don’t?
The Bitcoin Network
Peer-to-Peer Network Architecture
Bitcoin is structured as a peer-to-peer network architecture on top of the internet. The term peer-to-peer, or P2P, means that the computers that participate in the network are peers to each other, that they are all equal, that there are no "special" nodes, and that all nodes share the burden of providing network services. The network nodes interconnect in a mesh network with a "flat" topology. There is no server, no centralized service, and no hierarchy within the network. Nodes in a P2P network both provide and consume services at the same time with reciprocity acting as the incentive for participation. P2P networks are inherently resilient, decentralized, and open. A preeminent example of a P2P network architecture was the early internet itself, where nodes on the IP network were equal. Today’s internet architecture is more hierarchical, but the Internet Protocol still retains its flat-topology essence. Beyond bitcoin, the largest and most successful application of P2P technologies is file sharing, with Napster as the pioneer and BitTorrent as the most recent evolution of the architecture.
Bitcoin’s P2P network architecture is much more than a topology choice. Bitcoin is a P2P digital cash system by design, and the network architecture is both a reflection and a foundation of that core characteristic. Decentralization of control is a core design principle that can only be achieved and maintained by a flat, decentralized P2P consensus network.
The term "bitcoin network" refers to the collection of nodes running the bitcoin P2P protocol. In addition to the bitcoin P2P protocol, there are other protocols such as Stratum that are used for mining and lightweight or mobile wallets. These additional protocols are provided by gateway routing servers that access the bitcoin network using the bitcoin P2P protocol and then extend that network to nodes running other protocols. For example, Stratum servers connect Stratum mining nodes via the Stratum protocol to the main bitcoin network and bridge the Stratum protocol to the bitcoin P2P protocol. We use the term "extended bitcoin network" to refer to the overall network that includes the bitcoin P2P protocol, pool-mining protocols, the Stratum protocol, and any other related protocols connecting the components of the bitcoin system.
Node Types and Roles
Although nodes in the bitcoin P2P network are equal, they may take on different roles depending on the functionality they are supporting. A bitcoin node is a collection of functions: routing, the blockchain database, mining, and wallet services. A full node with all four of these functions is shown in [full_node_reference].
All nodes include the routing function to participate in the network and might include other functionality. All nodes validate and propagate transactions and blocks, and discover and maintain connections to peers. In the full-node example in [full_node_reference], the routing function is indicated by an orange circle named "Network Routing Node" or with the letter "N."
Some nodes, called full nodes, also maintain a complete and up-to-date copy of the blockchain. Full nodes can autonomously and authoritatively verify any transaction without external reference. Some nodes maintain only a subset of the blockchain and verify transactions using a method called simplified payment verification, or SPV. These nodes are known as SPV nodes or lightweight nodes. In the full-node example in the figure, the full-node blockchain database function is indicated by a blue circle called "Full Blockchain" or the letter "B." In [bitcoin_network], SPV nodes are drawn without the blue circle, showing that they do not have a full copy of the blockchain.
Mining nodes compete to create new blocks by running specialized hardware to solve the Proof-of-Work algorithm. Some mining nodes are also full nodes, maintaining a full copy of the blockchain, while others are lightweight nodes participating in pool mining and depending on a pool server to maintain a full node. The mining function is shown in the full node as a black circle called "Miner" or the letter "M."
User wallets might be part of a full node, as is usually the case with desktop bitcoin clients. Increasingly, many user wallets, especially those running on resource-constrained devices such as smartphones, are SPV nodes. The wallet function is shown in [full_node_reference] as a green circle called "Wallet" or the letter "W."
In addition to the main node types on the bitcoin P2P protocol, there are servers and nodes running other protocols, such as specialized mining pool protocols and lightweight client-access protocols.
[node_type_ledgend] shows the most common node types on the extended bitcoin network.
The Extended Bitcoin Network
The main bitcoin network, running the bitcoin P2P protocol, consists of between 5,000 and 8,000 listening nodes running various versions of the bitcoin reference client (Bitcoin Core) and a few hundred nodes running various other implementations of the bitcoin P2P protocol, such as Bitcoin Classic, Bitcoin Unlimited, BitcoinJ, Libbitcoin, btcd, and bcoin. A small percentage of the nodes on the bitcoin P2P network are also mining nodes, competing in the mining process, validating transactions, and creating new blocks. Various large companies interface with the bitcoin network by running full-node clients based on the Bitcoin Core client, with full copies of the blockchain and a network node, but without mining or wallet functions. These nodes act as network edge routers, allowing various other services (exchanges, wallets, block explorers, merchant payment processing) to be built on top.
The extended bitcoin network includes the network running the bitcoin P2P protocol, described earlier, as well as nodes running specialized protocols. Attached to the main bitcoin P2P network are a number of pool servers and protocol gateways that connect nodes running other protocols. These other protocol nodes are mostly pool mining nodes (see [mining]) and lightweight wallet clients, which do not carry a full copy of the blockchain.
[bitcoin_network] shows the extended bitcoin network with the various types of nodes, gateway servers, edge routers, and wallet clients and the various protocols they use to connect to each other.
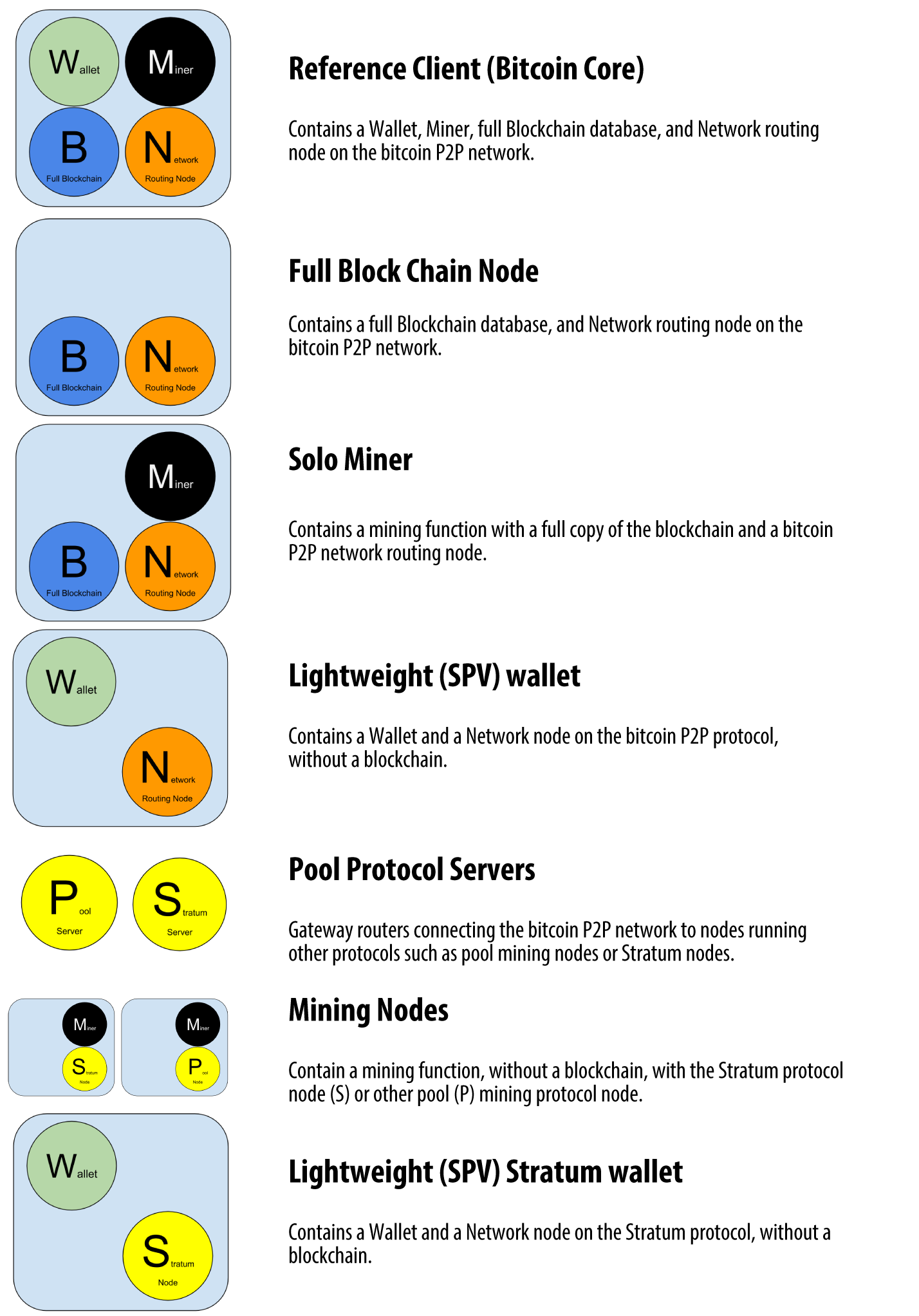
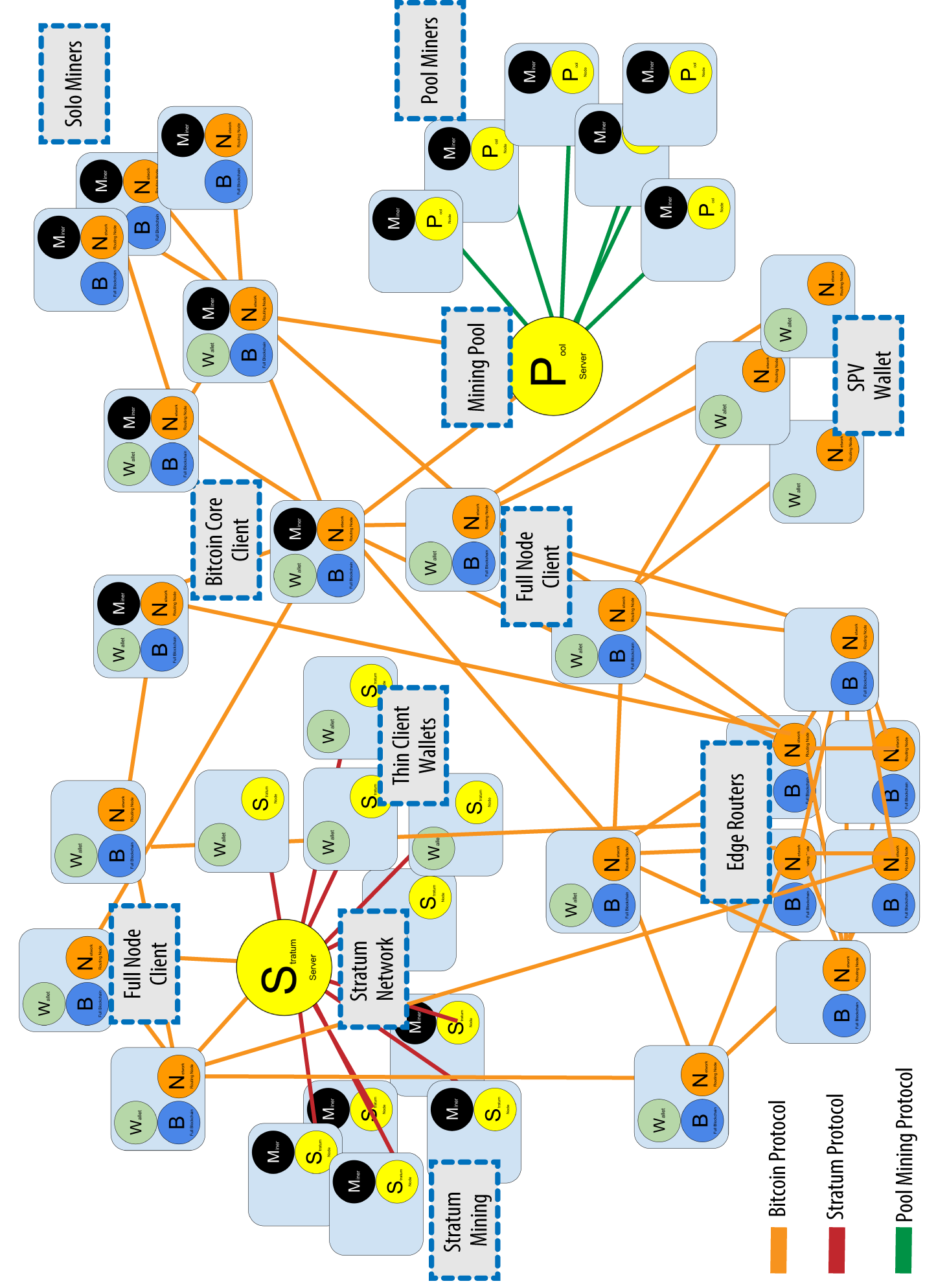
Bitcoin Relay Networks
While the bitcoin P2P network serves the general needs of a broad variety of node types, it exhibits too high network latency for the specialized needs of bitcoin mining nodes.
Bitcoin miners are engaged in a time-sensitive competition to solve the Proof-of-Work problem and extend the blockchain (see [mining]). While participating in this competition, bitcoin miners must minimize the time between the propagation of a winning block and the beginning of the next round of competition. In mining, network latency is directly related to profit margins.
A Bitcoin Relay Network is a network that attempts to minimize the latency in the transmission of blocks between miners. The original Bitcoin Relay Network was created by core developer Matt Corallo in 2015 to enable fast synchronization of blocks between miners with very low latency. The network consisted of several specialized nodes hosted on the Amazon Web Services infrastructure around the world and served to connect the majority of miners and mining pools.
The original Bitcoin Relay Network was replaced in 2016 with the introduction of the Fast Internet Bitcoin Relay Engine or FIBRE, also created by core developer Matt Corallo. FIBRE is a UDP-based relay network that relays blocks within a network of nodes. FIBRE implements compact block optimization to further reduce the amount of data transmitted and the network latency.
Another relay network (still in the proposal phase) is Falcon, based on research at Cornell University. Falcon uses "cut-through-routing" instead of "store-and-forward" to reduce latency by propagating parts of blocks as they are received rather than waiting until a complete block is received.
Relay networks are not replacements for bitcoin’s P2P network. Instead they are overlay networks that provide additional connectivity between nodes with specialized needs. Like freeways are not replacements for rural roads, but rather shortcuts between two points with heavy traffic, you still need small roads to connect to the freeways.
Network Discovery
When a new node boots up, it must discover other bitcoin nodes on the network in order to participate. To start this process, a new node must discover at least one existing node on the network and connect to it. The geographic location of other nodes is irrelevant; the bitcoin network topology is not geographically defined. Therefore, any existing bitcoin nodes can be selected at random.
To connect to a known peer, nodes establish a TCP connection, usually to port 8333 (the port generally known as the one used by bitcoin), or an alternative port if one is provided. Upon establishing a connection, the node will start a "handshake" (see [network_handshake]) by transmitting a version message, which contains basic identifying information, including:
-
nVersion -
The bitcoin P2P protocol version the client "speaks" (e.g., 70002)
-
nLocalServices -
A list of local services supported by the node, currently just
NODE_NETWORK -
nTime -
The current time
-
addrYou -
The IP address of the remote node as seen from this node
-
addrMe -
The IP address of the local node, as discovered by the local node
-
subver -
A sub-version showing the type of software running on this node (e.g.,
/Satoshi:0.9.2.1/) -
BestHeight -
The block height of this node’s blockchain
(See GitHub for an example of the version network message.)
The version message is always the first message sent by any peer to another peer. The local peer receiving a version message will examine the remote peer’s reported nVersion and decide if the remote peer is compatible. If the remote peer is compatible, the local peer will acknowledge the version message and establish a connection by sending a verack.
How does a new node find peers? The first method is to query DNS using a number of "DNS seeds," which are DNS servers that provide a list of IP addresses of bitcoin nodes. Some of those DNS seeds provide a static list of IP addresses of stable bitcoin listening nodes. Some of the DNS seeds are custom implementations of BIND (Berkeley Internet Name Daemon) that return a random subset from a list of bitcoin node addresses collected by a crawler or a long-running bitcoin node. The Bitcoin Core client contains the names of five different DNS seeds. The diversity of ownership and diversity of implementation of the different DNS seeds offers a high level of reliability for the initial bootstrapping process. In the Bitcoin Core client, the option to use the DNS seeds is controlled by the option switch -dnsseed (set to 1 by default, to use the DNS seed).
Alternatively, a bootstrapping node that knows nothing of the network must be given the IP address of at least one bitcoin node, after which it can establish connections through further introductions. The command-line argument -seednode can be used to connect to one node just for introductions using it as a seed. After the initial seed node is used to form introductions, the client will disconnect from it and use the newly discovered peers.
Once one or more connections are established, the new node will send an addr message containing its own IP address to its neighbors. The neighbors will, in turn, forward the addr message to their neighbors, ensuring that the newly connected node becomes well known and better connected. Additionally, the newly connected node can send getaddr to the neighbors, asking them to return a list of IP addresses of other peers. That way, a node can find peers to connect to and advertise its existence on the network for other nodes to find it. [address_propagation] shows the address discovery protocol.
A node must connect to a few different peers in order to establish diverse paths into the bitcoin network. Paths are not reliable—nodes come and go—and so the node must continue to discover new nodes as it loses old connections as well as assist other nodes when they bootstrap. Only one connection is needed to bootstrap, because the first node can offer introductions to its peer nodes and those peers can offer further introductions. It’s also unnecessary and wasteful of network resources to connect to more than a handful of nodes. After bootstrapping, a node will remember its most recent successful peer connections, so that if it is rebooted it can quickly reestablish connections with its former peer network. If none of the former peers respond to its connection request, the node can use the seed nodes to bootstrap again.
On a node running the Bitcoin Core client, you can list the peer connections with the command getpeerinfo:
$ bitcoin-cli getpeerinfo
[ { "addr" : "85.213.199.39:8333", "services" : "00000001", "lastsend" : 1405634126, "lastrecv" : 1405634127, "bytessent" : 23487651, "bytesrecv" : 138679099, "conntime" : 1405021768, "pingtime" : 0.00000000, "version" : 70002, "subver" : "/Satoshi:0.9.2.1/", "inbound" : false, "startingheight" : 310131, "banscore" : 0, "syncnode" : true }, { "addr" : "58.23.244.20:8333", "services" : "00000001", "lastsend" : 1405634127, "lastrecv" : 1405634124, "bytessent" : 4460918, "bytesrecv" : 8903575, "conntime" : 1405559628, "pingtime" : 0.00000000, "version" : 70001, "subver" : "/Satoshi:0.8.6/", "inbound" : false, "startingheight" : 311074, "banscore" : 0, "syncnode" : false } ]
To override the automatic management of peers and to specify a list of IP addresses, users can provide the option -connect=<IPAddress> and specify one or more IP addresses. If this option is used, the node will only connect to the selected IP addresses, instead of discovering and maintaining the peer connections automatically.
If there is no traffic on a connection, nodes will periodically send a message to maintain the connection. If a node has not communicated on a connection for more than 90 minutes, it is assumed to be disconnected and a new peer will be sought. Thus, the network dynamically adjusts to transient nodes and network problems, and can organically grow and shrink as needed without any central control.
Full Nodes
Full nodes are nodes that maintain a full blockchain with all transactions. More accurately, they probably should be called "full blockchain nodes." In the early years of bitcoin, all nodes were full nodes and currently the Bitcoin Core client is a full blockchain node. In the past two years, however, new forms of bitcoin clients have been introduced that do not maintain a full blockchain but run as lightweight clients. We’ll examine these in more detail in the next section.
Full blockchain nodes maintain a complete and up-to-date copy of the bitcoin blockchain with all the transactions, which they independently build and verify, starting with the very first block (genesis block) and building up to the latest known block in the network. A full blockchain node can independently and authoritatively verify any transaction without recourse or reliance on any other node or source of information. The full blockchain node relies on the network to receive updates about new blocks of transactions, which it then verifies and incorporates into its local copy of the blockchain.
Running a full blockchain node gives you the pure bitcoin experience: independent verification of all transactions without the need to rely on, or trust, any other systems. It’s easy to tell if you’re running a full node because it requires 20+ gigabytes of persistent storage (disk space) to store the full blockchain. If you need a lot of disk and it takes two to three days to sync to the network, you are running a full node. That is the price of complete independence and freedom from central authority.
There are a few alternative implementations of full blockchain bitcoin clients, built using different programming languages and software architectures. However, the most common implementation is the reference client Bitcoin Core, also known as the Satoshi client. More than 75% of the nodes on the bitcoin network run various versions of Bitcoin Core. It is identified as "Satoshi" in the sub-version string sent in the version message and shown by the command getpeerinfo as we saw earlier; for example, /Satoshi:0.8.6/.
Exchanging "Inventory"
The first thing a full node will do once it connects to peers is try to construct a complete blockchain. If it is a brand-new node and has no blockchain at all, it only knows one block, the genesis block, which is statically embedded in the client software. Starting with block #0 (the genesis block), the new node will have to download hundreds of thousands of blocks to synchronize with the network and reestablish the full blockchain.
The process of syncing the blockchain starts with the version message, because that contains BestHeight, a node’s current blockchain height (number of blocks). A node will see the version messages from its peers, know how many blocks they each have, and be able to compare to how many blocks it has in its own blockchain. Peered nodes will exchange a getblocks message that contains the hash (fingerprint) of the top block on their local blockchain. One of the peers will be able to identify the received hash as belonging to a block that is not at the top, but rather belongs to an older block, thus deducing that its own local blockchain is longer than its peer’s.
The peer that has the longer blockchain has more blocks than the other node and can identify which blocks the other node needs in order to "catch up." It will identify the first 500 blocks to share and transmit their hashes using an inv (inventory) message. The node missing these blocks will then retrieve them, by issuing a series of getdata messages requesting the full block data and identifying the requested blocks using the hashes from the inv message.
Let’s assume, for example, that a node only has the genesis block. It will then receive an inv message from its peers containing the hashes of the next 500 blocks in the chain. It will start requesting blocks from all of its connected peers, spreading the load and ensuring that it doesn’t overwhelm any peer with requests. The node keeps track of how many blocks are "in transit" per peer connection, meaning blocks that it has requested but not received, checking that it does not exceed a limit (MAX_BLOCKS_IN_TRANSIT_PER_PEER). This way, if it needs a lot of blocks, it will only request new ones as previous requests are fulfilled, allowing the peers to control the pace of updates and not overwhelm the network. As each block is received, it is added to the blockchain, as we will see in [blockchain]. As the local blockchain is gradually built up, more blocks are requested and received, and the process continues until the node catches up to the rest of the network.
This process of comparing the local blockchain with the peers and retrieving any missing blocks happens any time a node goes offline for any period of time. Whether a node has been offline for a few minutes and is missing a few blocks, or a month and is missing a few thousand blocks, it starts by sending getblocks, gets an inv response, and starts downloading the missing blocks. [inventory_synchronization] shows the inventory and block propagation protocol.
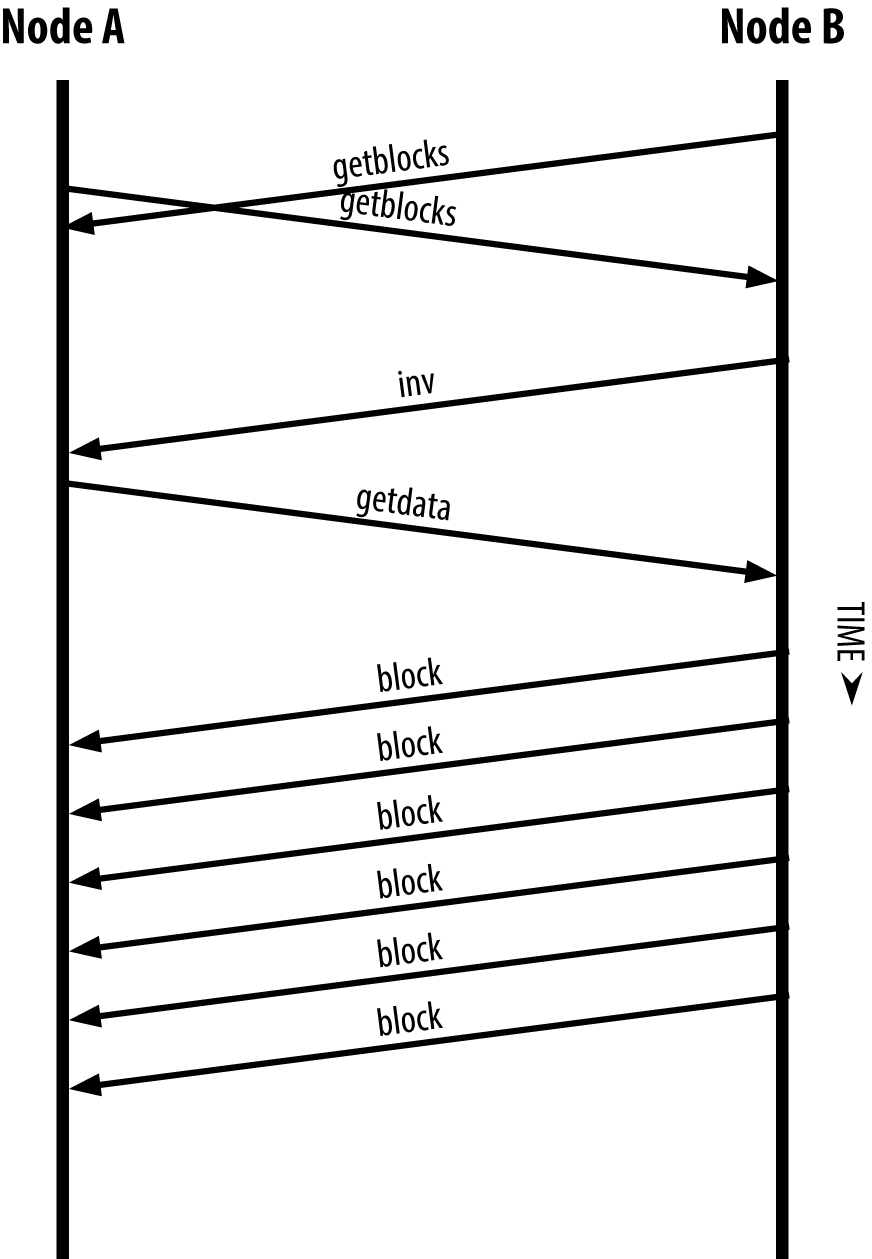
Simplified Payment Verification (SPV) Nodes
Not all nodes have the ability to store the full blockchain. Many bitcoin clients are designed to run on space- and power-constrained devices, such as smartphones, tablets, or embedded systems. For such devices, a simplified payment verification (SPV) method is used to allow them to operate without storing the full blockchain. These types of clients are called SPV clients or lightweight clients. As bitcoin adoption surges, the SPV node is becoming the most common form of bitcoin node, especially for bitcoin wallets.
SPV nodes download only the block headers and do not download the transactions included in each block. The resulting chain of blocks, without transactions, is 1,000 times smaller than the full blockchain. SPV nodes cannot construct a full picture of all the UTXOs that are available for spending because they do not know about all the transactions on the network. SPV nodes verify transactions using a slightly different methodology that relies on peers to provide partial views of relevant parts of the blockchain on demand.
As an analogy, a full node is like a tourist in a strange city, equipped with a detailed map of every street and every address. By comparison, an SPV node is like a tourist in a strange city asking random strangers for turn-by-turn directions while knowing only one main avenue. Although both tourists can verify the existence of a street by visiting it, the tourist without a map doesn’t know what lies down any of the side streets and doesn’t know what other streets exist. Positioned in front of 23 Church Street, the tourist without a map cannot know if there are a dozen other "23 Church Street" addresses in the city and whether this is the right one. The mapless tourist’s best chance is to ask enough people and hope some of them are not trying to mug him.
SPV verifies transactions by reference to their depth in the blockchain instead of their height. Whereas a full blockchain node will construct a fully verified chain of thousands of blocks and transactions reaching down the blockchain (back in time) all the way to the genesis block, an SPV node will verify the chain of all blocks (but not all transactions) and link that chain to the transaction of interest.
For example, when examining a transaction in block 300,000, a full node links all 300,000 blocks down to the genesis block and builds a full database of UTXO, establishing the validity of the transaction by confirming that the UTXO remains unspent. An SPV node cannot validate whether the UTXO is unspent. Instead, the SPV node will establish a link between the transaction and the block that contains it, using a merkle path (see [merkle_trees]). Then, the SPV node waits until it sees the six blocks 300,001 through 300,006 piled on top of the block containing the transaction and verifies it by establishing its depth under blocks 300,006 to 300,001. The fact that other nodes on the network accepted block 300,000 and then did the necessary work to produce six more blocks on top of it is proof, by proxy, that the transaction was not a double-spend.
An SPV node cannot be persuaded that a transaction exists in a block when the transaction does not in fact exist. The SPV node establishes the existence of a transaction in a block by requesting a merkle path proof and by validating the Proof-of-Work in the chain of blocks. However, a transaction’s existence can be "hidden" from an SPV node. An SPV node can definitely prove that a transaction exists but cannot verify that a transaction, such as a double-spend of the same UTXO, doesn’t exist because it doesn’t have a record of all transactions. This vulnerability can be used in a denial-of-service attack or for a double-spending attack against SPV nodes. To defend against this, an SPV node needs to connect randomly to several nodes, to increase the probability that it is in contact with at least one honest node. This need to randomly connect means that SPV nodes also are vulnerable to network partitioning attacks or Sybil attacks, where they are connected to fake nodes or fake networks and do not have access to honest nodes or the real bitcoin network.
For most practical purposes, well-connected SPV nodes are secure enough, striking a balance between resource needs, practicality, and security. For infallible security, however, nothing beats running a full blockchain node.
|
Tip
|
A full blockchain node verifies a transaction by checking the entire chain of thousands of blocks below it in order to guarantee that the UTXO is not spent, whereas an SPV node checks how deep the block is buried by a handful of blocks above it. |
To get the block headers, SPV nodes use a getheaders message instead of getblocks. The responding peer will send up to 2,000 block headers using a single headers message. The process is otherwise the same as that used by a full node to retrieve full blocks. SPV nodes also set a filter on the connection to peers, to filter the stream of future blocks and transactions sent by the peers. Any transactions of interest are retrieved using a getdata request. The peer generates a tx message containing the transactions, in response. [spv_synchronization] shows the synchronization of block headers.
Because SPV nodes need to retrieve specific transactions in order to selectively verify them, they also create a privacy risk. Unlike full blockchain nodes, which collect all transactions within each block, the SPV node’s requests for specific data can inadvertently reveal the addresses in their wallet. For example, a third party monitoring a network could keep track of all the transactions requested by a wallet on an SPV node and use those to associate bitcoin addresses with the user of that wallet, destroying the user’s privacy.
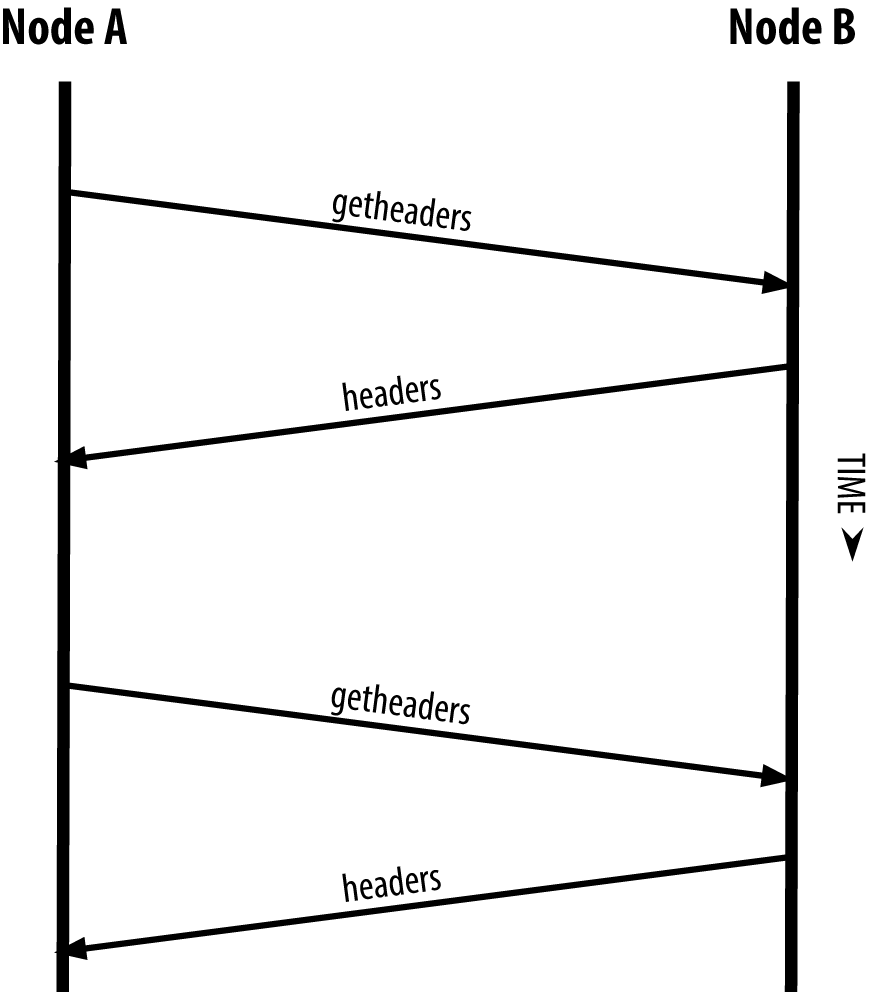
Shortly after the introduction of SPV/lightweight nodes, bitcoin developers added a feature called bloom filters to address the privacy risks of SPV nodes. Bloom filters allow SPV nodes to receive a subset of the transactions without revealing precisely which addresses they are interested in, through a filtering mechanism that uses probabilities rather than fixed patterns.
Bloom Filters
A bloom filter is a probabilistic search filter, a way to describe a desired pattern without specifying it exactly. Bloom filters offer an efficient way to express a search pattern while protecting privacy. They are used by SPV nodes to ask their peers for transactions matching a specific pattern, without revealing exactly which addresses, keys, or transactions they are searching for.
In our previous analogy, a tourist without a map is asking for directions to a specific address, "23 Church St." If she asks strangers for directions to this street, she inadvertently reveals her destination. A bloom filter is like asking, "Are there any streets in this neighborhood whose name ends in R-C-H?" A question like that reveals slightly less about the desired destination than asking for "23 Church St." Using this technique, a tourist could specify the desired address in more detail such as "ending in U-R-C-H" or less detail as "ending in H." By varying the precision of the search, the tourist reveals more or less information, at the expense of getting more or less specific results. If she asks a less specific pattern, she gets a lot more possible addresses and better privacy, but many of the results are irrelevant. If she asks for a very specific pattern, she gets fewer results but loses privacy.
Bloom filters serve this function by allowing an SPV node to specify a search pattern for transactions that can be tuned toward precision or privacy. A more specific bloom filter will produce accurate results, but at the expense of revealing what patterns the SPV node is interested in, thus revealing the addresses owned by the user’s wallet. A less specific bloom filter will produce more data about more transactions, many irrelevant to the node, but will allow the node to maintain better privacy.
How Bloom Filters Work
Bloom filters are implemented as a variable-size array of N binary digits (a bit field) and a variable number of M hash functions. The hash functions are designed to always produce an output that is between 1 and N, corresponding to the array of binary digits. The hash functions are generated deterministically, so that any node implementing a bloom filter will always use the same hash functions and get the same results for a specific input. By choosing different length (N) bloom filters and a different number (M) of hash functions, the bloom filter can be tuned, varying the level of accuracy and therefore privacy.
In [bloom1], we use a very small array of 16 bits and a set of three hash functions to demonstrate how bloom filters work.
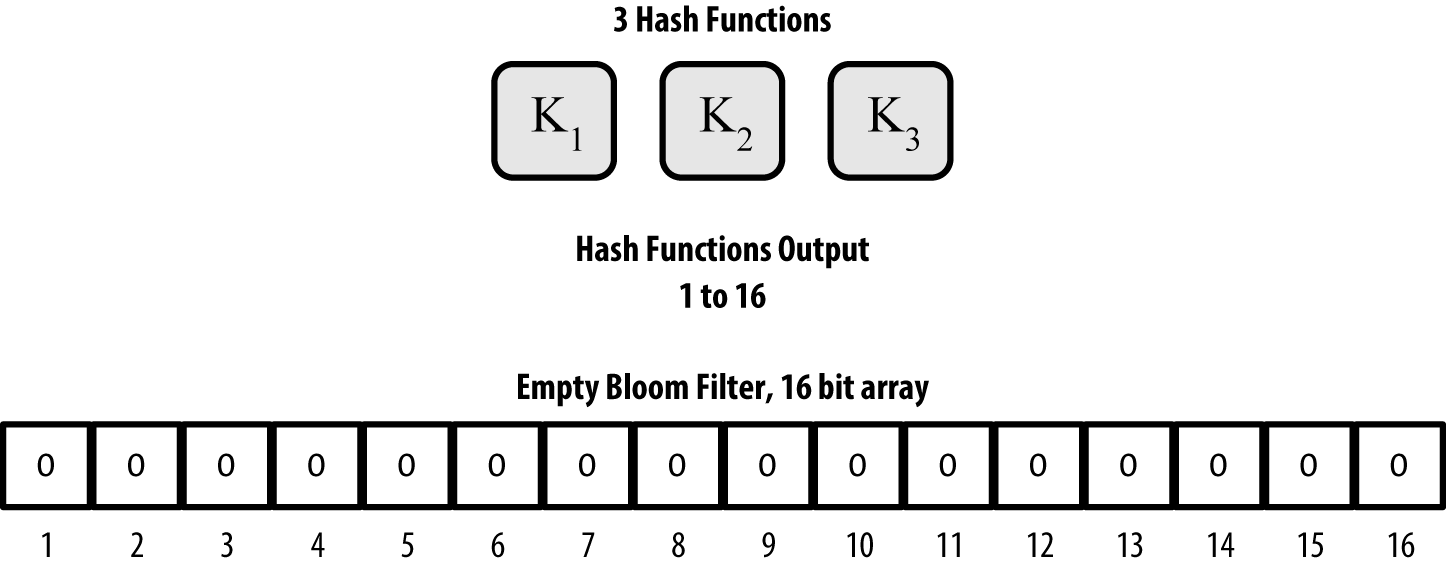
The bloom filter is initialized so that the array of bits is all zeros. To add a pattern to the bloom filter, the pattern is hashed by each hash function in turn. Applying the first hash function to the input results in a number between 1 and N. The corresponding bit in the array (indexed from 1 to N) is found and set to 1, thereby recording the output of the hash function. Then, the next hash function is used to set another bit and so on. Once all M hash functions have been applied, the search pattern will be "recorded" in the bloom filter as M bits that have been changed from 0 to 1.
Adding a second pattern is as simple as repeating this process. The pattern is hashed by each hash function in turn and the result is recorded by setting the bits to 1. Note that as a bloom filter is filled with more patterns, a hash function result might coincide with a bit that is already set to 1, in which case the bit is not changed. In essence, as more patterns record on overlapping bits, the bloom filter starts to become saturated with more bits set to 1 and the accuracy of the filter decreases. This is why the filter is a probabilistic data structure—it gets less accurate as more patterns are added. The accuracy depends on the number of patterns added versus the size of the bit array (N) and number of hash functions (M). A larger bit array and more hash functions can record more patterns with higher accuracy. A smaller bit array or fewer hash functions will record fewer patterns and produce less accuracy.
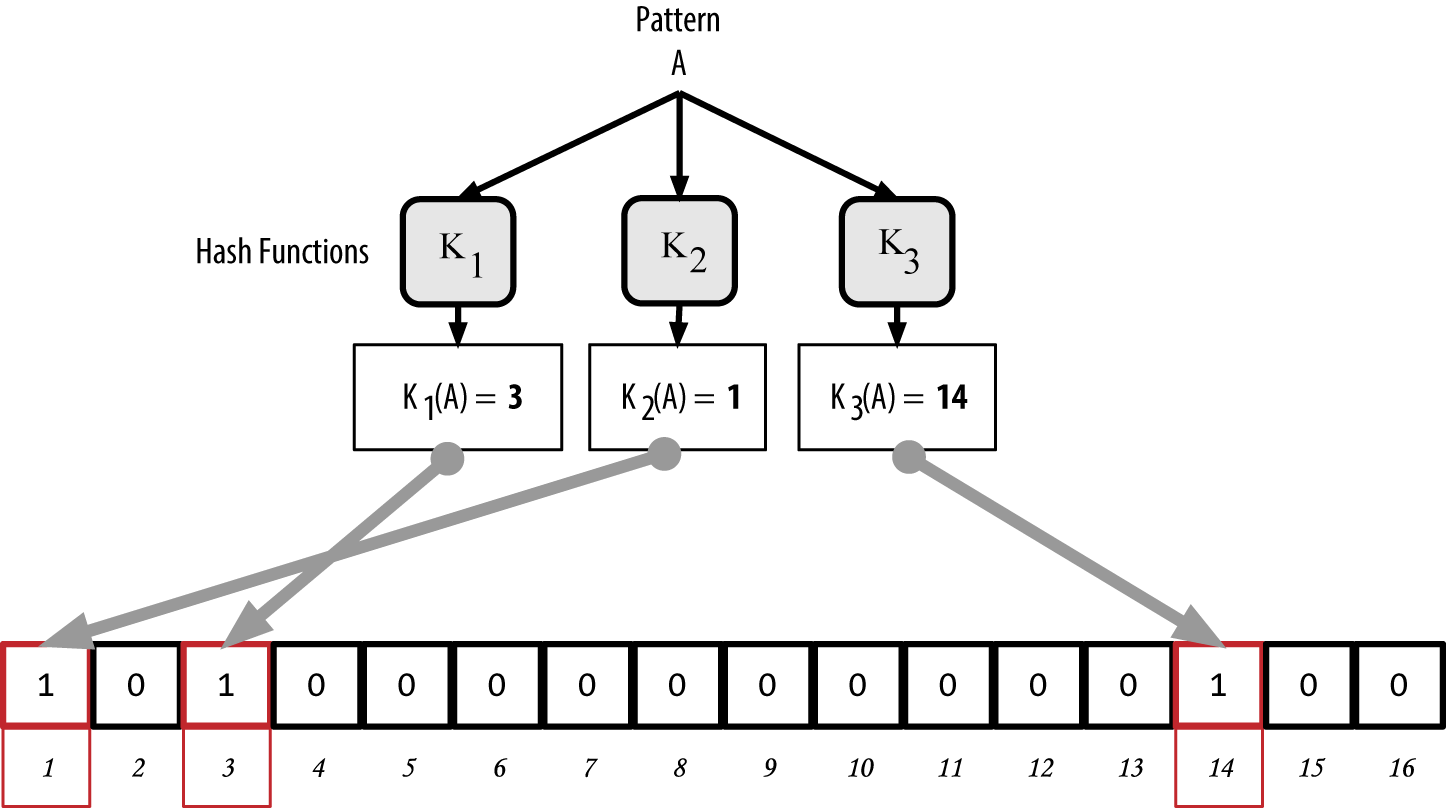
[bloom3] is an example of adding a second pattern "B" to the simple bloom filter.
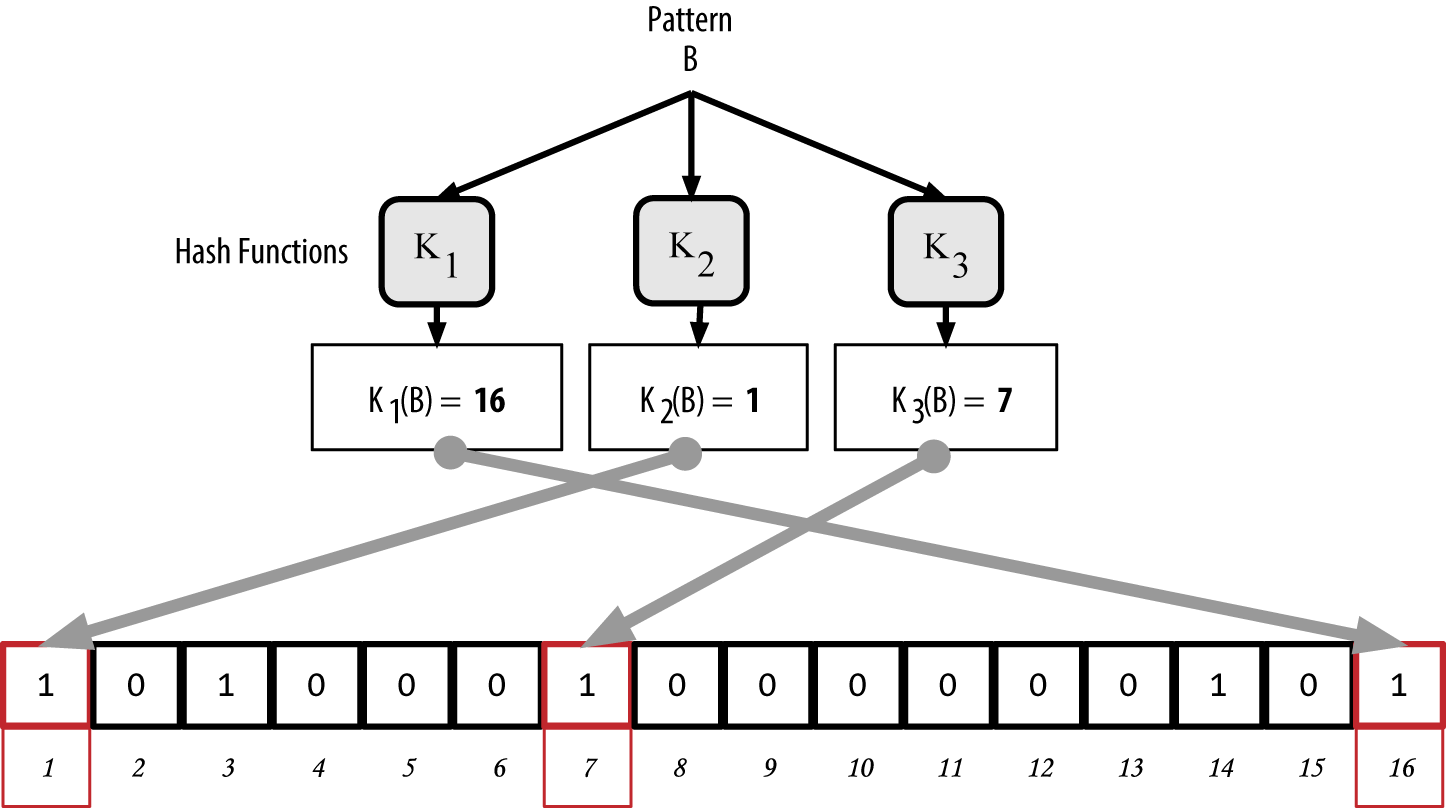
To test if a pattern is part of a bloom filter, the pattern is hashed by each hash function and the resulting bit pattern is tested against the bit array. If all the bits indexed by the hash functions are set to 1, then the pattern is probably recorded in the bloom filter. Because the bits may be set because of overlap from multiple patterns, the answer is not certain, but is rather probabilistic. In simple terms, a bloom filter positive match is a "Maybe, Yes."
[bloom4] is an example of testing the existence of pattern "X" in the simple bloom filter. The corresponding bits are set to 1, so the pattern is probably a match.
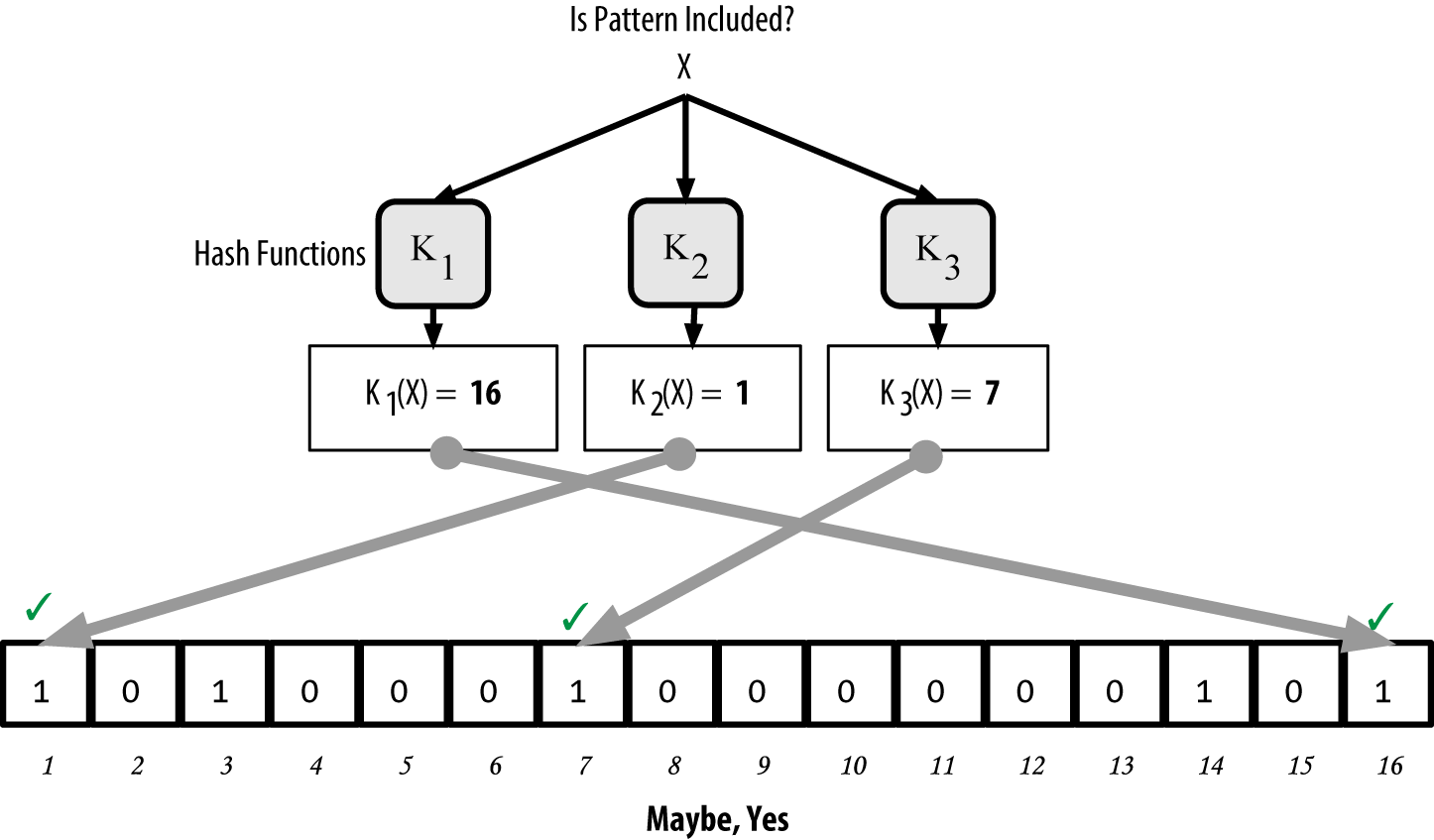
On the contrary, if a pattern is tested against the bloom filter and any one of the bits is set to 0, this proves that the pattern was not recorded in the bloom filter. A negative result is not a probability, it is a certainty. In simple terms, a negative match on a bloom filter is a "Definitely Not!"
[bloom5] is an example of testing the existence of pattern "Y" in the simple bloom filter. One of the corresponding bits is set to 0, so the pattern is definitely not a match.
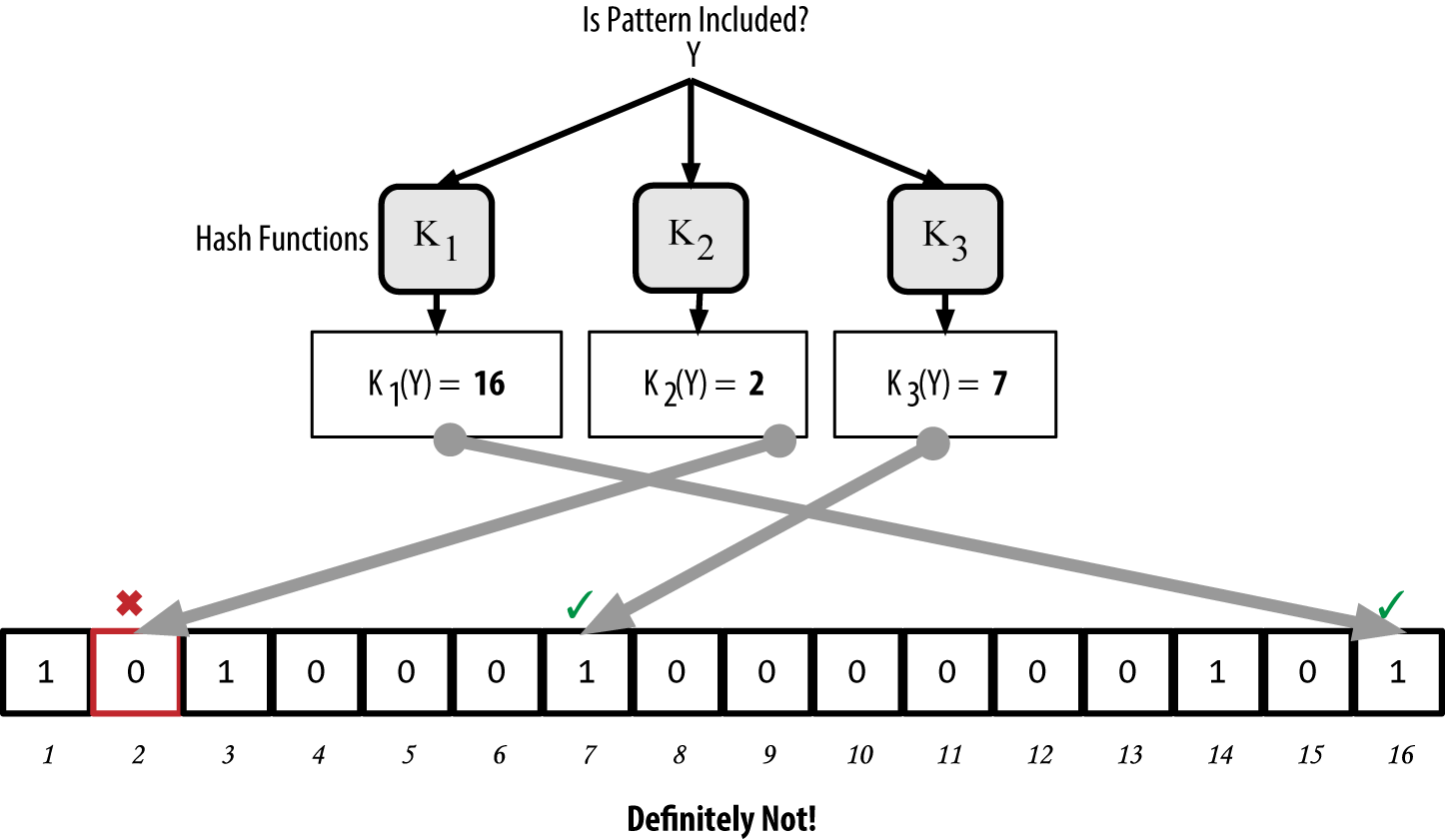
How SPV Nodes Use Bloom Filters
Bloom filters are used to filter the transactions (and blocks containing them) that an SPV node receives from its peers, selecting only transactions of interest to the SPV node without revealing which addresses or keys it is interested in.
An SPV node will initialize a bloom filter as "empty"; in that state the bloom filter will not match any patterns. The SPV node will then make a list of all the addresses, keys, and hashes that it is interested in. It will do this by extracting the public key hash and script hash and transaction IDs from any UTXO controlled by its wallet. The SPV node then adds each of these to the bloom filter, so that the bloom filter will "match" if these patterns are present in a transaction, without revealing the patterns themselves.
The SPV node will then send a filterload message to the peer, containing the bloom filter to use on the connection. On the peer, bloom filters are checked against each incoming transaction. The full node checks several parts of the transaction against the bloom filter, looking for a match including:
-
The transaction ID
-
The data components from the locking scripts of each of the transaction outputs (every key and hash in the script)
-
Each of the transaction inputs
-
Each of the input signature data components (or witness scripts)
By checking against all these components, bloom filters can be used to match public key hashes, scripts, OP_RETURN values, public keys in signatures, or any future component of a smart contract or complex script.
After a filter is established, the peer will then test each transaction’s outputs against the bloom filter. Only transactions that match the filter are sent to the node.
In response to a getdata message from the node, peers will send a merkleblock message that contains only block headers for blocks matching the filter and a merkle path (see [merkle_trees]) for each matching transaction. The peer will then also send tx messages containing the transactions matched by the filter.
As the full node sends transactions to the SPV node, the SPV node discards any false positives and uses the correctly matched transactions to update its UTXO set and wallet balance. As it updates its own view of the UTXO set, it also modifies the bloom filter to match any future transactions referencing the UTXO it just found. The full node then uses the new bloom filter to match new transactions and the whole process repeats.
The node setting the bloom filter can interactively add patterns to the filter by sending a filteradd message. To clear the bloom filter, the node can send a filterclear message. Because it is not possible to remove a pattern from a bloom filter, a node has to clear and resend a new bloom filter if a pattern is no longer desired.
The network protocol and bloom filter mechanism for SPV nodes is defined in BIP-37 (Peer Services).
SPV Nodes and Privacy
Nodes that implement SPV have weaker privacy than a full node. A full node receives all transactions and therefore reveals no information about whether it is using some address in its wallet. An SPV node receives a filtered list of transactions related to the addresses that are in its wallet. As a result, it reduces the privacy of the owner.
Bloom filters are a way to reduce the loss of privacy. Without them, an SPV node would have to explicitly list the addresses it was interested in, creating a serious breach of privacy. However, even with bloom filters, an adversary monitoring the traffic of an SPV client or connected to it directly as a node in the P2P network can collect enough information over time to learn the addresses in the wallet of the SPV client.
Encrypted and Authenticated Connections
Most new users of bitcoin assume that the network communications of a bitcoin node are encrypted. In fact, the original implementation of bitcoin communicates entirely in the clear. While this is not a major privacy concern for full nodes, it is a big problem for SPV nodes.
As a way to increase the privacy and security of the bitcoin P2P network, there are two solutions that provide encryption of the communications: Tor Transport and P2P Authentication and Encryption with BIP-150/151.
Tor Transport
Tor, which stands for The Onion Routing network, is a software project and network that offers encryption and encapsulation of data through randomized network paths that offer anonymity, untraceability and privacy.
Bitcoin Core offers several configuration options that allow you to run a bitcoin node with its traffic transported over the Tor network. In addition, Bitcoin Core can also offer a Tor hidden service allowing other Tor nodes to connect to your node directly over Tor.
As of Bitcoin Core version 0.12, a node will offer a hidden Tor service automatically if it is able to connect to a local Tor service. If you have Tor installed and the Bitcoin Core process runs as a user with adequate permissions to access the Tor authentication cookie, it should work automatically. Use the debug flag to turn on Bitcoin Core’s debugging for the Tor service like this:
$ bitcoind --daemon --debug=torYou should see "tor: ADD_ONION successful" in the logs, indicating that Bitcoin Core has added a hidden service to the Tor network.
You can find more instructions on running Bitcoin Core as a Tor hidden service in the Bitcoin Core documentation (docs/tor.md) and various online tutorials.
Peer-to-Peer Authentication and Encryption
Two Bitcoin Improvement Proposals, BIP-150 and BIP-151, add support for P2P authentication and encryption in the bitcoin P2P network. These two BIPs define optional services that may be offered by compatible bitcoin nodes. BIP-151 enables negotiated encryption for all communications between two nodes that support BIP-151. BIP-150 offers optional peer authentication that allows nodes to authenticate each other’s identity using ECDSA and private keys. BIP-150 requires that prior to authentication the two nodes have established encrypted communications as per BIP-151.
As of January 2017, BIP-150 and BIP-151 are not implemented in Bitcoin Core. However, the two proposals have been implemented by at least one alternative bitcoin client named bcoin.
BIP-150 and BIP-151 allow users to run SPV clients that connect to a trusted full node, using encryption and authentication to protect the privacy of the SPV client.
Additionally, authentication can be used to create networks of trusted bitcoin nodes and prevent Man-in-the-Middle attacks. Finally, P2P encryption, if deployed broadly, would strengthen the resistance of bitcoin to traffic analysis and privacy-eroding surveillance, especially in totalitarian countries where internet use is heavily controlled and monitored.
The standard is defined in BIP-150 (Peer Authentication) and BIP-151 (Peer-to-Peer Communication Encryption).
Transaction Pools
Almost every node on the bitcoin network maintains a temporary list of unconfirmed transactions called the memory pool, mempool, or transaction pool. Nodes use this pool to keep track of transactions that are known to the network but are not yet included in the blockchain. For example, a wallet node will use the transaction pool to track incoming payments to the user’s wallet that have been received on the network but are not yet confirmed.
As transactions are received and verified, they are added to the transaction pool and relayed to the neighboring nodes to propagate on the network.
Some node implementations also maintain a separate pool of orphaned transactions. If a transaction’s inputs refer to a transaction that is not yet known, such as a missing parent, the orphan transaction will be stored temporarily in the orphan pool until the parent transaction arrives.
When a transaction is added to the transaction pool, the orphan pool is checked for any orphans that reference this transaction’s outputs (its children). Any matching orphans are then validated. If valid, they are removed from the orphan pool and added to the transaction pool, completing the chain that started with the parent transaction. In light of the newly added transaction, which is no longer an orphan, the process is repeated recursively looking for any further descendants, until no more descendants are found. Through this process, the arrival of a parent transaction triggers a cascade reconstruction of an entire chain of interdependent transactions by re-uniting the orphans with their parents all the way down the chain.
Both the transaction pool and orphan pool (where implemented) are stored in local memory and are not saved on persistent storage; rather, they are dynamically populated from incoming network messages. When a node starts, both pools are empty and are gradually populated with new transactions received on the network.
Some implementations of the bitcoin client also maintain a UTXO database or pool, which is the set of all unspent outputs on the blockchain. Although the name "UTXO pool" sounds similar to the transaction pool, it represents a different set of data. Unlike the transaction and orphan pools, the UTXO pool is not initialized empty but instead contains millions of entries of unspent transaction outputs, everything that is unspent from all the way back to the genesis block. The UTXO pool may be housed in local memory or as an indexed database table on persistent storage.
Whereas the transaction and orphan pools represent a single node’s local perspective and might vary significantly from node to node depending upon when the node was started or restarted, the UTXO pool represents the emergent consensus of the network and therefore will vary little between nodes. Furthermore, the transaction and orphan pools only contain unconfirmed transactions, while the UTXO pool only contains confirmed outputs.
The Blockchain
Introduction
The blockchain data structure is an ordered, back-linked list of blocks of transactions. The blockchain can be stored as a flat file, or in a simple database. The Bitcoin Core client stores the blockchain metadata using Google’s LevelDB database. Blocks are linked "back," each referring to the previous block in the chain. The blockchain is often visualized as a vertical stack, with blocks layered on top of each other and the first block serving as the foundation of the stack. The visualization of blocks stacked on top of each other results in the use of terms such as "height" to refer to the distance from the first block, and "top" or "tip" to refer to the most recently added block.
Each block within the blockchain is identified by a hash, generated using the SHA256 cryptographic hash algorithm on the header of the block. Each block also references a previous block, known as the parent block, through the "previous block hash" field in the block header. In other words, each block contains the hash of its parent inside its own header. The sequence of hashes linking each block to its parent creates a chain going back all the way to the first block ever created, known as the genesis block.
Although a block has just one parent, it can temporarily have multiple children. Each of the children refers to the same block as its parent and contains the same (parent) hash in the "previous block hash" field. Multiple children arise during a blockchain "fork," a temporary situation that occurs when different blocks are discovered almost simultaneously by different miners (see [forks]). Eventually, only one child block becomes part of the blockchain and the "fork" is resolved. Even though a block may have more than one child, each block can have only one parent. This is because a block has one single "previous block hash" field referencing its single parent.
The "previous block hash" field is inside the block header and thereby affects the current block’s hash. The child’s own identity changes if the parent’s identity changes. When the parent is modified in any way, the parent’s hash changes. The parent’s changed hash necessitates a change in the "previous block hash" pointer of the child. This in turn causes the child’s hash to change, which requires a change in the pointer of the grandchild, which in turn changes the grandchild, and so on. This cascade effect ensures that once a block has many generations following it, it cannot be changed without forcing a recalculation of all subsequent blocks. Because such a recalculation would require enormous computation (and therefore energy consumption), the existence of a long chain of blocks makes the blockchain’s deep history immutable, which is a key feature of bitcoin’s security.
One way to think about the blockchain is like layers in a geological formation, or glacier core sample. The surface layers might change with the seasons, or even be blown away before they have time to settle. But once you go a few inches deep, geological layers become more and more stable. By the time you look a few hundred feet down, you are looking at a snapshot of the past that has remained undisturbed for millions of years. In the blockchain, the most recent few blocks might be revised if there is a chain recalculation due to a fork. The top six blocks are like a few inches of topsoil. But once you go more deeply into the blockchain, beyond six blocks, blocks are less and less likely to change. After 100 blocks back there is so much stability that the coinbase transaction—the transaction containing newly mined bitcoin—can be spent. A few thousand blocks back (a month) and the blockchain is settled history, for all practical purposes. While the protocol always allows a chain to be undone by a longer chain and while the possibility of any block being reversed always exists, the probability of such an event decreases as time passes until it becomes infinitesimal.
Structure of a Block
A block is a container data structure that aggregates transactions for inclusion in the public ledger, the blockchain. The block is made of a header, containing metadata, followed by a long list of transactions that make up the bulk of its size. The block header is 80 bytes, whereas the average transaction is at least 250 bytes and the average block contains more than 500 transactions. A complete block, with all transactions, is therefore 1,000 times larger than the block header. [block_structure1] describes the structure of a block.
| Size | Field | Description |
|---|---|---|
4 bytes |
Block Size |
The size of the block, in bytes, following this field |
80 bytes |
Block Header |
Several fields form the block header |
1–9 bytes (VarInt) |
Transaction Counter |
How many transactions follow |
Variable |
Transactions |
The transactions recorded in this block |
Block Header
The block header consists of three sets of block metadata. First, there is a reference to a previous block hash, which connects this block to the previous block in the blockchain. The second set of metadata, namely the difficulty, timestamp, and nonce, relate to the mining competition, as detailed in [mining]. The third piece of metadata is the merkle tree root, a data structure used to efficiently summarize all the transactions in the block. [block_header_structure_ch09] describes the structure of a block header.
| Size | Field | Description |
|---|---|---|
4 bytes |
Version |
A version number to track software/protocol upgrades |
32 bytes |
Previous Block Hash |
A reference to the hash of the previous (parent) block in the chain |
32 bytes |
Merkle Root |
A hash of the root of the merkle tree of this block’s transactions |
4 bytes |
Timestamp |
The approximate creation time of this block (seconds from Unix Epoch) |
4 bytes |
Difficulty Target |
The Proof-of-Work algorithm difficulty target for this block |
4 bytes |
Nonce |
A counter used for the Proof-of-Work algorithm |
The nonce, difficulty target, and timestamp are used in the mining process and will be discussed in more detail in [mining].
Block Identifiers: Block Header Hash and Block Height
The primary identifier of a block is its cryptographic hash, a digital fingerprint, made by hashing the block header twice through the SHA256 algorithm. The resulting 32-byte hash is called the block hash but is more accurately the block header hash, because only the block header is used to compute it. For example, 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f is the block hash of the first bitcoin block ever created. The block hash identifies a block uniquely and unambiguously and can be independently derived by any node by simply hashing the block header.
Note that the block hash is not actually included inside the block’s data structure, neither when the block is transmitted on the network, nor when it is stored on a node’s persistence storage as part of the blockchain. Instead, the block’s hash is computed by each node as the block is received from the network. The block hash might be stored in a separate database table as part of the block’s metadata, to facilitate indexing and faster retrieval of blocks from disk.
A second way to identify a block is by its position in the blockchain, called the block height. The first block ever created is at block height 0 (zero) and is the same block that was previously referenced by the following block hash 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f. A block can thus be identified two ways: by referencing the block hash or by referencing the block height. Each subsequent block added "on top" of that first block is one position "higher" in the blockchain, like boxes stacked one on top of the other. The block height on January 1, 2017 was approximately 446,000, meaning there were 446,000 blocks stacked on top of the first block created in January 2009.
Unlike the block hash, the block height is not a unique identifier. Although a single block will always have a specific and invariant block height, the reverse is not true—the block height does not always identify a single block. Two or more blocks might have the same block height, competing for the same position in the blockchain. This scenario is discussed in detail in the section [forks]. The block height is also not a part of the block’s data structure; it is not stored within the block. Each node dynamically identifies a block’s position (height) in the blockchain when it is received from the bitcoin network. The block height might also be stored as metadata in an indexed database table for faster retrieval.
|
Tip
|
A block’s block hash always identifies a single block uniquely. A block also always has a specific block height. However, it is not always the case that a specific block height can identify a single block. Rather, two or more blocks might compete for a single position in the blockchain. |
The Genesis Block
The first block in the blockchain is called the genesis block and was created in 2009. It is the common ancestor of all the blocks in the blockchain, meaning that if you start at any block and follow the chain backward in time, you will eventually arrive at the genesis block.
Every node always starts with a blockchain of at least one block because the genesis block is statically encoded within the bitcoin client software, such that it cannot be altered. Every node always "knows" the genesis block’s hash and structure, the fixed time it was created, and even the single transaction within. Thus, every node has the starting point for the blockchain, a secure "root" from which to build a trusted blockchain.
See the statically encoded genesis block inside the Bitcoin Core client, in chainparams.cpp.
The following identifier hash belongs to the genesis block:
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26fYou can search for that block hash in any block explorer website, such as blockchain.info, and you will find a page describing the contents of this block, with a URL containing that hash:
Using the Bitcoin Core reference client on the command line:
$ bitcoin-cli getblock 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f{ "hash" : "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f", "confirmations" : 308321, "size" : 285, "height" : 0, "version" : 1, "merkleroot" : "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b", "tx" : [ "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b" ], "time" : 1231006505, "nonce" : 2083236893, "bits" : "1d00ffff", "difficulty" : 1.00000000, "nextblockhash" : "00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048" }
The genesis block contains a hidden message within it. The coinbase transaction input contains the text "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks." This message was intended to offer proof of the earliest date this block was created, by referencing the headline of the British newspaper The Times. It also serves as a tongue-in-cheek reminder of the importance of an independent monetary system, with bitcoin’s launch occurring at the same time as an unprecedented worldwide monetary crisis. The message was embedded in the first block by Satoshi Nakamoto, bitcoin’s creator.
Linking Blocks in the Blockchain
Bitcoin full nodes maintain a local copy of the blockchain, starting at the genesis block. The local copy of the blockchain is constantly updated as new blocks are found and used to extend the chain. As a node receives incoming blocks from the network, it will validate these blocks and then link them to the existing blockchain. To establish a link, a node will examine the incoming block header and look for the "previous block hash."
Let’s assume, for example, that a node has 277,314 blocks in the local copy of the blockchain. The last block the node knows about is block 277,314, with a block header hash of:
00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249The bitcoin node then receives a new block from the network, which it parses as follows:
{ "size" : 43560, "version" : 2, "previousblockhash" : "00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249", "merkleroot" : "5e049f4030e0ab2debb92378f53c0a6e09548aea083f3ab25e1d94ea1155e29d", "time" : 1388185038, "difficulty" : 1180923195.25802612, "nonce" : 4215469401, "tx" : [ "257e7497fb8bc68421eb2c7b699dbab234831600e7352f0d9e6522c7cf3f6c77", #[... many more transactions omitted ...] "05cfd38f6ae6aa83674cc99e4d75a1458c165b7ab84725eda41d018a09176634" ] }
Looking at this new block, the node finds the previousblockhash field, which contains the hash of its parent block. It is a hash known to the node, that of the last block on the chain at height 277,314. Therefore, this new block is a child of the last block on the chain and extends the existing blockchain. The node adds this new block to the end of the chain, making the blockchain longer with a new height of 277,315. [chain_of_blocks] shows the chain of three blocks, linked by references in the previousblockhash field.
Merkle Trees
Each block in the bitcoin blockchain contains a summary of all the transactions in the block using a merkle tree.
A merkle tree, also known as a binary hash tree, is a data structure used for efficiently summarizing and verifying the integrity of large sets of data. Merkle trees are binary trees containing cryptographic hashes. The term "tree" is used in computer science to describe a branching data structure, but these trees are usually displayed upside down with the "root" at the top and the "leaves" at the bottom of a diagram, as you will see in the examples that follow.
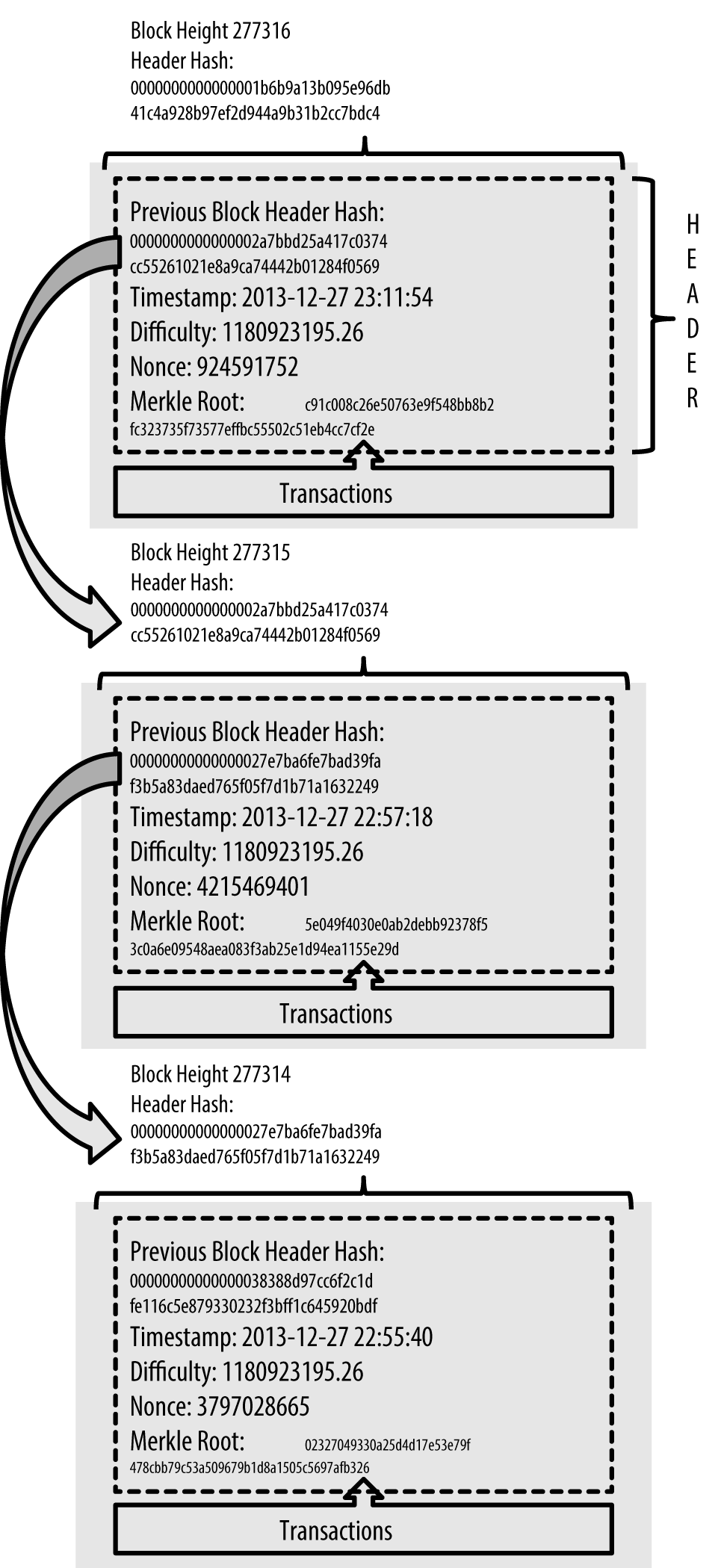
Merkle trees are used in bitcoin to summarize all the transactions in a block, producing an overall digital fingerprint of the entire set of transactions, providing a very efficient process to verify whether a transaction is included in a block. A merkle tree is constructed by recursively hashing pairs of nodes until there is only one hash, called the root, or merkle root. The cryptographic hash algorithm used in bitcoin’s merkle trees is SHA256 applied twice, also known as double-SHA256.
When N data elements are hashed and summarized in a merkle tree, you can check to see if any one data element is included in the tree with at most 2*log2(N) calculations, making this a very efficient data structure.
The merkle tree is constructed bottom-up. In the following example, we start with four transactions, A, B, C, and D, which form the leaves of the merkle tree, as shown in [simple_merkle]. The transactions are not stored in the merkle tree; rather, their data is hashed and the resulting hash is stored in each leaf node as HA, HB, HC, and HD:
HA = SHA256(SHA256(Transaction A))
Consecutive pairs of leaf nodes are then summarized in a parent node, by concatenating the two hashes and hashing them together. For example, to construct the parent node HAB, the two 32-byte hashes of the children are concatenated to create a 64-byte string. That string is then double-hashed to produce the parent node’s hash:
HAB = SHA256(SHA256(HA + HB))
The process continues until there is only one node at the top, the node known as the merkle root. That 32-byte hash is stored in the block header and summarizes all the data in all four transactions. [simple_merkle] shows how the root is calculated by pair-wise hashes of the nodes.
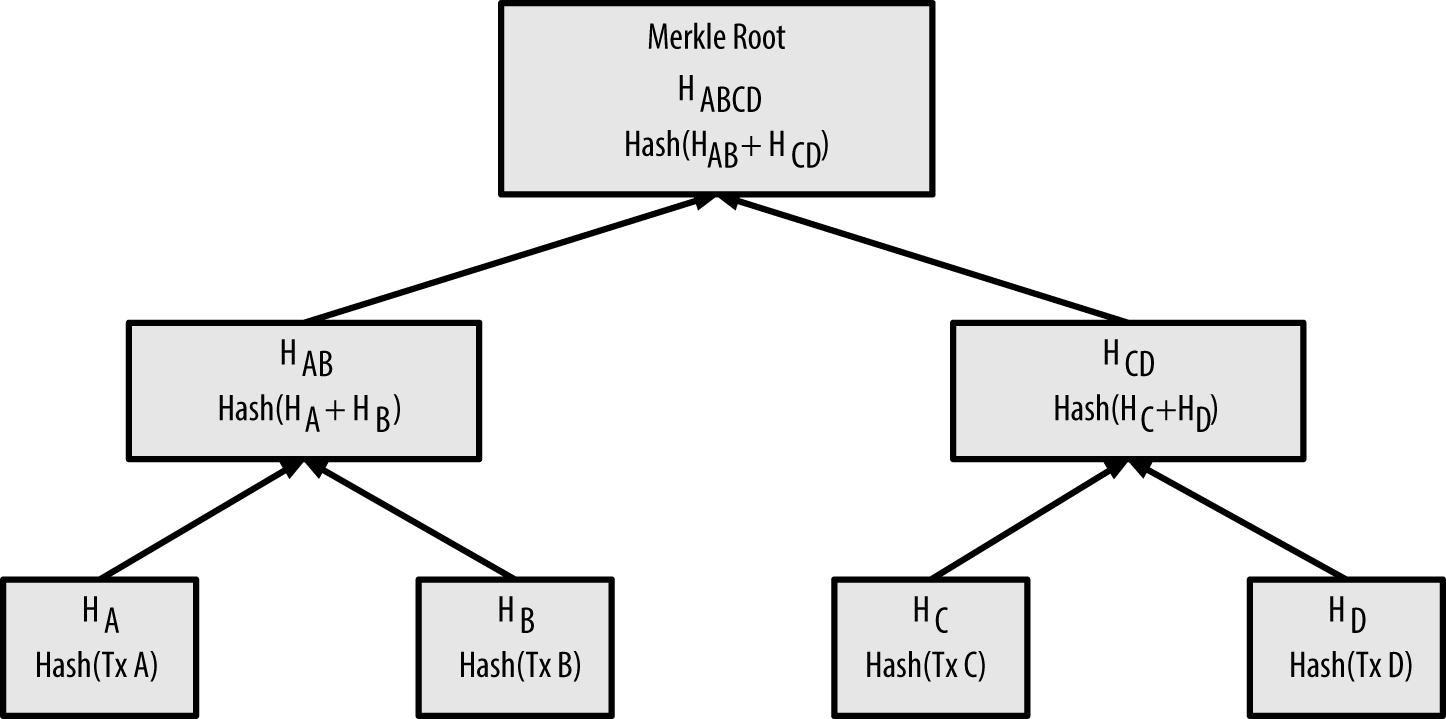
Because the merkle tree is a binary tree, it needs an even number of leaf nodes. If there is an odd number of transactions to summarize, the last transaction hash will be duplicated to create an even number of leaf nodes, also known as a balanced tree. This is shown in [merkle_tree_odd], where transaction C is duplicated.
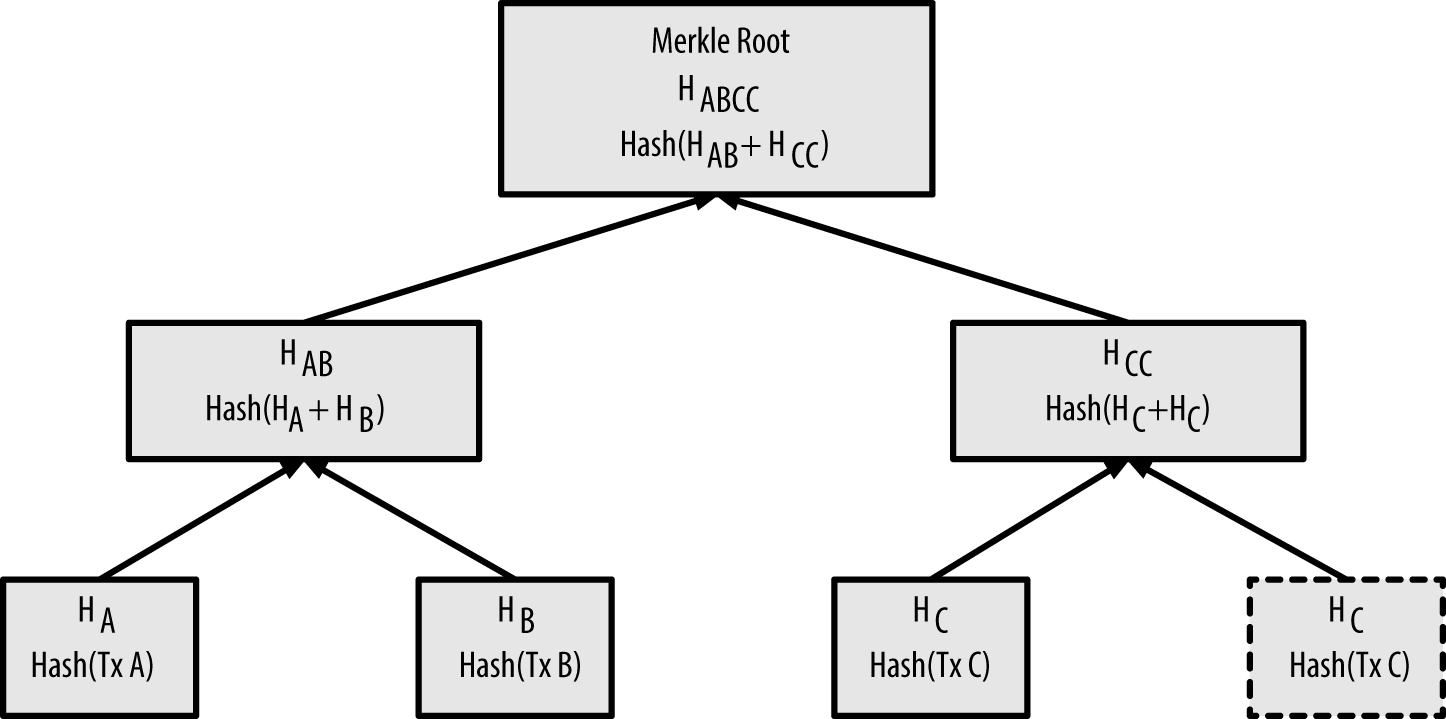
The same method for constructing a tree from four transactions can be generalized to construct trees of any size. In bitcoin it is common to have several hundred to more than a thousand transactions in a single block, which are summarized in exactly the same way, producing just 32 bytes of data as the single merkle root. In [merkle_tree_large], you will see a tree built from 16 transactions. Note that although the root looks bigger than the leaf nodes in the diagram, it is the exact same size, just 32 bytes. Whether there is one transaction or a hundred thousand transactions in the block, the merkle root always summarizes them into 32 bytes.
To prove that a specific transaction is included in a block, a node only needs to produce log2(N) 32-byte hashes, constituting an authentication path or merkle path connecting the specific transaction to the root of the tree. This is especially important as the number of transactions increases, because the base-2 logarithm of the number of transactions increases much more slowly. This allows bitcoin nodes to efficiently produce paths of 10 or 12 hashes (320–384 bytes), which can provide proof of a single transaction out of more than a thousand transactions in a megabyte-size block.
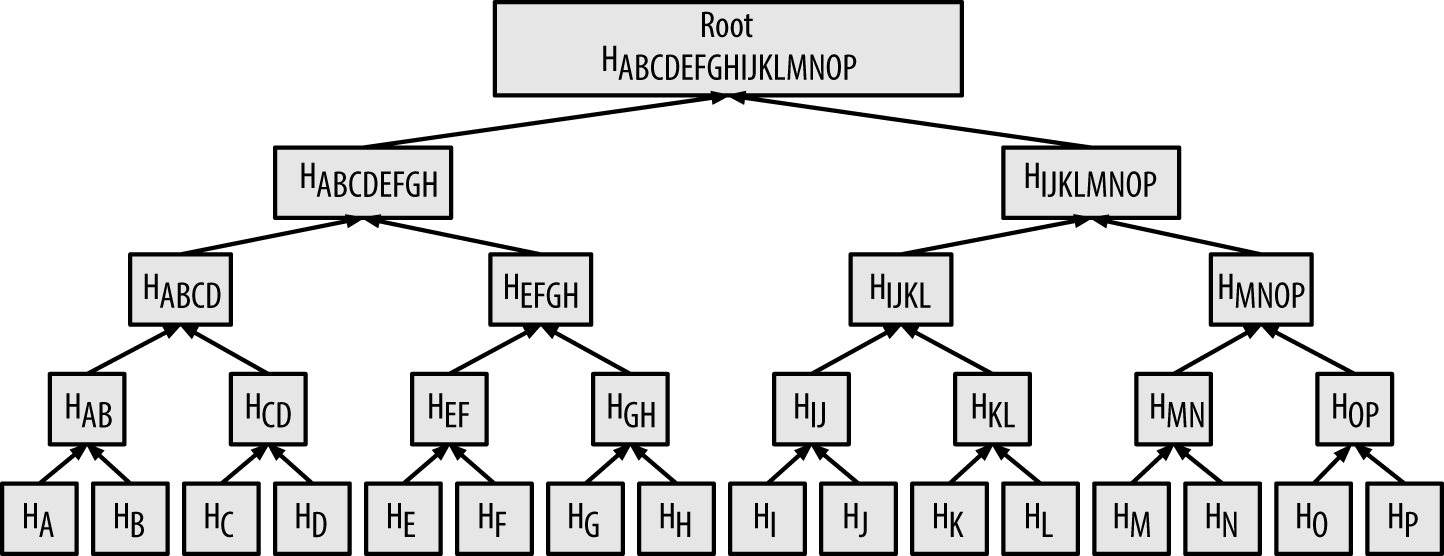
In [merkle_tree_path], a node can prove that a transaction K is included in the block by producing a merkle path that is only four 32-byte hashes long (128 bytes total). The path consists of the four hashes (shown with a shaded background in [merkle_tree_path]) HL, HIJ, HMNOP, and HABCDEFGH. With those four hashes provided as an authentication path, any node can prove that HK (with a black background at the bottom of the diagram) is included in the merkle root by computing four additional pair-wise hashes HKL, HIJKL, HIJKLMNOP, and the merkle tree root (outlined in a dashed line in the diagram).
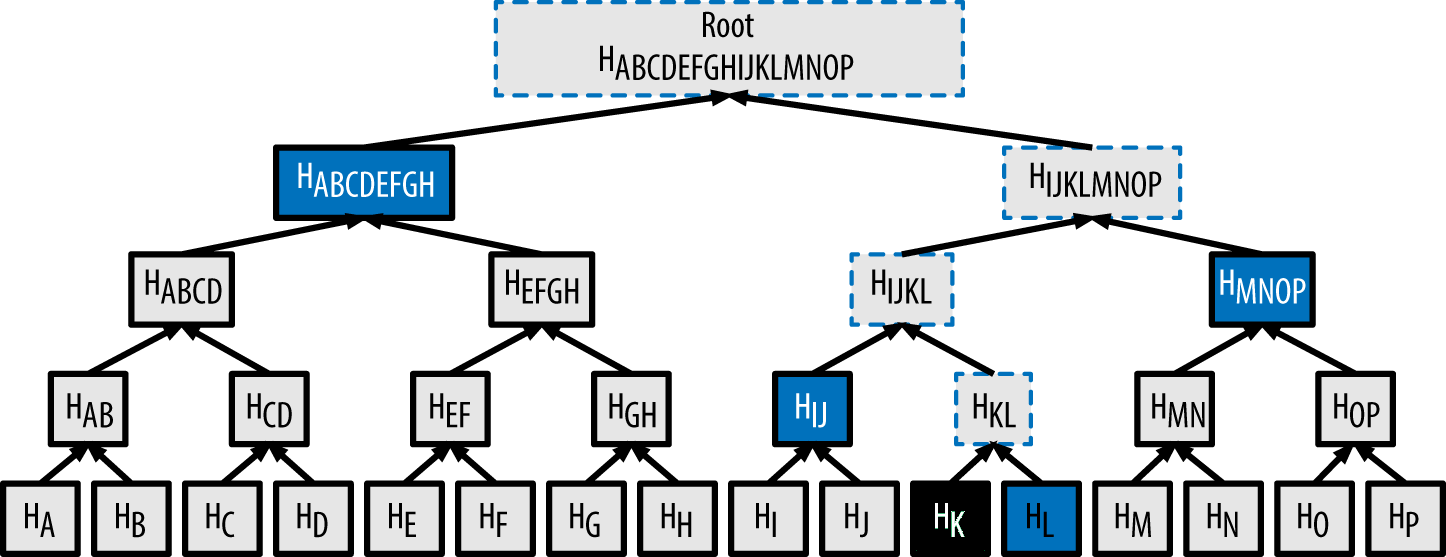
The code in [merkle_example] demonstrates the process of creating a merkle tree from the leaf-node hashes up to the root, using the libbitcoin library for some helper functions.
#include <bitcoin/bitcoin.hpp> bc::hash_digest create_merkle(bc::hash_list& merkle) { // Stop if hash list is empty. if (merkle.empty()) return bc::null_hash; else if (merkle.size() == 1) return merkle[0]; // While there is more than 1 hash in the list, keep looping... while (merkle.size() > 1) { // If number of hashes is odd, duplicate last hash in the list. if (merkle.size() % 2 != 0) merkle.push_back(merkle.back()); // List size is now even. assert(merkle.size() % 2 == 0); // New hash list. bc::hash_list new_merkle; // Loop through hashes 2 at a time. for (auto it = merkle.begin(); it != merkle.end(); it += 2) { // Join both current hashes together (concatenate). bc::data_chunk concat_data(bc::hash_size * 2); auto concat = bc::make_serializer(concat_data.begin()); concat.write_hash(*it); concat.write_hash(*(it + 1)); assert(concat.iterator() == concat_data.end()); // Hash both of the hashes. bc::hash_digest new_root = bc::bitcoin_hash(concat_data); // Add this to the new list. new_merkle.push_back(new_root); } // This is the new list. merkle = new_merkle; // DEBUG output ------------------------------------- std::cout << "Current merkle hash list:" << std::endl; for (const auto& hash: merkle) std::cout << " " << bc::encode_hex(hash) << std::endl; std::cout << std::endl; // -------------------------------------------------- } // Finally we end up with a single item. return merkle[0]; } int main() { // Replace these hashes with ones from a block to reproduce the same merkle root. bc::hash_list tx_hashes{{ bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000000"), bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000011"), bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000022"), }}; const bc::hash_digest merkle_root = create_merkle(tx_hashes); std::cout << "Result: " << bc::encode_hex(merkle_root) << std::endl; return 0; }
[merkle_example_run] shows the result of compiling and running the merkle code.
$ # Compile the merkle.cpp code $ g++ -o merkle merkle.cpp $(pkg-config --cflags --libs libbitcoin) $ # Run the merkle executable $ ./merkle Current merkle hash list: 32650049a0418e4380db0af81788635d8b65424d397170b8499cdc28c4d27006 30861db96905c8dc8b99398ca1cd5bd5b84ac3264a4e1b3e65afa1bcee7540c4 Current merkle hash list: d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3 Result: d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3
The efficiency of merkle trees becomes obvious as the scale increases. [block_structure2] shows the amount of data that needs to be exchanged as a merkle path to prove that a transaction is part of a block.
| Number of transactions | Approx. size of block | Path size (hashes) | Path size (bytes) |
|---|---|---|---|
16 transactions |
4 kilobytes |
4 hashes |
128 bytes |
512 transactions |
128 kilobytes |
9 hashes |
288 bytes |
2048 transactions |
512 kilobytes |
11 hashes |
352 bytes |
65,535 transactions |
16 megabytes |
16 hashes |
512 bytes |
As you can see from the table, while the block size increases rapidly, from 4 KB with 16 transactions to a block size of 16 MB to fit 65,535 transactions, the merkle path required to prove the inclusion of a transaction increases much more slowly, from 128 bytes to only 512 bytes. With merkle trees, a node can download just the block headers (80 bytes per block) and still be able to identify a transaction’s inclusion in a block by retrieving a small merkle path from a full node, without storing or transmitting the vast majority of the blockchain, which might be several gigabytes in size. Nodes that do not maintain a full blockchain, called simplified payment verification (SPV) nodes, use merkle paths to verify transactions without downloading full blocks.
Merkle Trees and Simplified Payment Verification (SPV)
Merkle trees are used extensively by SPV nodes. SPV nodes don’t have all transactions and do not download full blocks, just block headers. In order to verify that a transaction is included in a block, without having to download all the transactions in the block, they use an authentication path, or merkle path.
Consider, for example, an SPV node that is interested in incoming payments to an address contained in its wallet. The SPV node will establish a bloom filter (see [bloom_filters]) on its connections to peers to limit the transactions received to only those containing addresses of interest. When a peer sees a transaction that matches the bloom filter, it will send that block using a merkleblock message. The merkleblock message contains the block header as well as a merkle path that links the transaction of interest to the merkle root in the block. The SPV node can use this merkle path to connect the transaction to the block and verify that the transaction is included in the block. The SPV node also uses the block header to link the block to the rest of the blockchain. The combination of these two links, between the transaction and block, and between the block and blockchain, proves that the transaction is recorded in the blockchain. All in all, the SPV node will have received less than a kilobyte of data for the block header and merkle path, an amount of data that is more than a thousand times less than a full block (about 1 megabyte currently).
Bitcoin’s Test Blockchains
You might be surprised to learn that there is more than one bitcoin blockchain. The "main" bitcoin blockchain, the one created by Satoshi Nakamoto on January 3rd, 2009, the one with the genesis block we studied in this chapter, is called mainnet. There are other bitcoin blockchains that are used for testing purposes: at this time testnet, segnet, and regtest. Let’s look at each in turn.
Testnet—Bitcoin’s Testing Playground
Testnet is the name of the test blockchain, network, and currency that is used for testing purposes. The testnet is a fully featured live P2P network, with wallets, test bitcoins (testnet coins), mining, and all the other features of mainnet. There are really only two differences: testnet coins are meant to be worthless and mining difficulty should be low enough that anyone can mine testnet coins relatively easily (keeping them worthless).
Any software development that is intended for production use on bitcoin’s mainnet should first be tested on testnet with test coins. This protects both the developers from monetary losses due to bugs and the network from unintended behavior due to bugs.
Keeping the coins worthless and the mining easy, however, is not easy. Despite pleas from developers, some people use advanced mining equipment (GPUs and ASICs) to mine on testnet. This increases the difficulty, makes it impossible to mine with a CPU, and eventually makes it difficult enough to get test coins that people start valuing them, so they’re not worthless. As a result, every now and then, the testnet has to be scrapped and restarted from a new genesis block, resetting the difficulty.
The current testnet is called testnet3, the third iteration of testnet, restarted in February 2011 to reset the difficulty from the previous testnet.
Keep in mind that testnet3 is a large blockchain, in excess of 20 GB in early 2017. It will take a day or so to sync fully and use up resources on your computer. Not as much as mainnet, but not exactly "lightweight" either. One good way to run a testnet node is as a virtual machine image (e.g., VirtualBox, Docker, Cloud Server, etc.) dedicated for that purpose.
Using testnet
Bitcoin Core, like almost all other bitcoin software, has full support for operation on testnet instead of mainnet, but also allows you to mine testnet coins and operate a full testnet node.
To start Bitcoin Core on testnet instead of mainnet you use the testnet switch:
$ bitcoind -testnetIn the logs you should see that bitcoind is building a new blockchain in the testnet3 subdirectory of the default bitcoind directory:
bitcoind: Using data directory /home/username/.bitcoin/testnet3To connect to bitcoind, you use the bitcoin-cli command-line tool, but you must also switch it to testnet mode:
$ bitcoin-cli -testnet getinfo
{
"version": 130200,
"protocolversion": 70015,
"walletversion": 130000,
"balance": 0.00000000,
"blocks": 416,
"timeoffset": 0,
"connections": 3,
"proxy": "",
"difficulty": 1,
"testnet": true,
"keypoololdest": 1484801486,
"keypoolsize": 100,
"paytxfee": 0.00000000,
"relayfee": 0.00001000,
"errors": ""
}You can also use the getblockchaininfo command to confirm the details of the testnet3 blockchain and your sync progress:
$ bitcoin-cli -testnet getblockchaininfo
{
"chain": "test",
"blocks": 1088,
"headers": 139999,
"bestblockhash": "0000000063d29909d475a1c4ba26da64b368e56cce5d925097bf3a2084370128",
"difficulty": 1,
"mediantime": 1337966158,
"verificationprogress": 0.001644065914099759,
"chainwork": "0000000000000000000000000000000000000000000000000000044104410441",
"pruned": false,
"softforks": [
[...]You can also run on testnet3 with other full-node implementations, such as btcd (written in Go) and bcoin (written in JavaScript), to experiment and learn in other programming languages and frameworks.
In early 2017, testnet3 supports all the features of mainnet, in addition to Segregated Witness (see [segwit]), which has yet to activate on mainnet. Therefore, testnet3 can also be used to test Segregated Witness features.
Segnet—The Segregated Witness Testnet
In 2016, a special-purpose testnet was launched to aid in development and testing of Segregated Witness (aka segwit; see [segwit]). This test blockchain is called segnet and can be joined by running a special version (branch) of Bitcoin Core.
Since segwit was added to testnet3, it is no longer necessary to use segnet for testing of segwit features.
In the future it is likely we will see other testnet blockchains that are specifically designed to test a single feature or major architectural change, like segnet.
Regtest—The Local Blockchain
Regtest, which stands for "Regression Testing," is a Bitcoin Core feature that allows you to create a local blockchain for testing purposes. Unlike testnet3, which is a public and shared test blockchain, the regtest blockchains are intended to be run as closed systems for local testing. You launch a regtest blockchain from scratch, creating a local genesis block. You may add other nodes to the network, or run it with a single node only to test the Bitcoin Core software.
To start Bitcoin Core in regtest mode, you use the regtest flag:
$ bitcoind -regtestJust like with testnet, Bitcoin Core will initialize a new blockchain under the regtest subdirectory of your bitcoind default directory:
bitcoind: Using data directory /home/username/.bitcoin/regtestTo use the command-line tool, you need to specify the regtest flag too. Let’s try the getblockchaininfo command to inspect the regtest blockchain:
$ bitcoin-cli -regtest getblockchaininfo
{
"chain": "regtest",
"blocks": 0,
"headers": 0,
"bestblockhash": "0f9188f13cb7b2c71f2a335e3a4fc328bf5beb436012afca590b1a11466e2206",
"difficulty": 4.656542373906925e-10,
"mediantime": 1296688602,
"verificationprogress": 1,
"chainwork": "0000000000000000000000000000000000000000000000000000000000000002",
"pruned": false,
[...]As you can see, there are no blocks yet. Let’s mine some (500 blocks) and earn the reward:
$ bitcoin-cli -regtest generate 500
[
"7afed70259f22c2bf11e406cb12ed5c0657b6e16a6477a9f8b28e2046b5ba1ca",
"1aca2f154a80a9863a9aac4c72047a6d3f385c4eec5441a4aafa6acaa1dada14",
"4334ecf6fb022f30fbd764c3ee778fabbd53b4a4d1950eae8a91f1f5158ed2d1",
"5f951d34065efeaf64e54e91d00b260294fcdfc7f05dbb5599aec84b957a7766",
"43744b5e77c1dfece9d05ab5f0e6796ebe627303163547e69e27f55d0f2b9353",
[...]
"6c31585a48d4fc2b3fd25521f4515b18aefb59d0def82bd9c2185c4ecb754327"
]It will only take a few seconds to mine all these blocks, which certainly makes it easy for testing. If you check your wallet balance, you will see that you earned reward for the first 400 blocks (coinbase rewards must be 100 blocks deep before you can spend them):
$ bitcoin-cli -regtest getbalance
12462.50000000Using Test Blockchains for Development
Bitcoin’s various blockchains (regtest, segnet, testnet3, mainnet) offer a range of testing environments for bitcoin development. Use the test blockchains whether you are developing for Bitcoin Core, or another full-node consensus client; an application such as a wallet, exchange, ecommerce site; or even developing novel smart contracts and complex scripts.
You can use the test blockchains to establish a development pipeline. Test your code locally on a regtest as you develop it. Once you are ready to try it on a public network, switch to testnet to expose your code to a more dynamic environment with more diversity of code and applications. Finally, once you are confident your code works as expected, switch to mainnet to deploy it in production. As you make changes, improvements, bug fixes, etc., start the pipeline again, deploying each change first on regtest, then on testnet, and finally into production.
Mining and Consensus
Introduction
The word "mining" is somewhat misleading. By evoking the extraction of precious metals, it focuses our attention on the reward for mining, the new bitcoin created in each block. Although mining is incentivized by this reward, the primary purpose of mining is not the reward or the generation of new coins. If you view mining only as the process by which coins are created, you are mistaking the means (incentives) as the goal of the process. Mining is the mechanism that underpins the decentralized clearinghouse, by which transactions are validated and cleared. Mining is the invention that makes bitcoin special, a decentralized security mechanism that is the basis for P2P digital cash.
Mining secures the bitcoin system and enables the emergence of network-wide consensus without a central authority. The reward of newly minted coins and transaction fees is an incentive scheme that aligns the actions of miners with the security of the network, while simultaneously implementing the monetary supply.
|
Tip
|
The purpose of mining is not the creation of new bitcoin. That’s the incentive system. Mining is the mechanism by which bitcoin’s security is decentralized. |
Miners validate new transactions and record them on the global ledger. A new block, containing transactions that occurred since the last block, is "mined" every 10 minutes on average, thereby adding those transactions to the blockchain. Transactions that become part of a block and added to the blockchain are considered "confirmed," which allows the new owners of bitcoin to spend the bitcoin they received in those transactions.
Miners receive two types of rewards in return for the security provided by mining: new coins created with each new block, and transaction fees from all the transactions included in the block. To earn this reward, miners compete to solve a difficult mathematical problem based on a cryptographic hash algorithm. The solution to the problem, called the Proof-of-Work, is included in the new block and acts as proof that the miner expended significant computing effort. The competition to solve the Proof-of-Work algorithm to earn the reward and the right to record transactions on the blockchain is the basis for bitcoin’s security model.
The process is called mining because the reward (new coin generation) is designed to simulate diminishing returns, just like mining for precious metals. Bitcoin’s money supply is created through mining, similar to how a central bank issues new money by printing bank notes. The maximum amount of newly created bitcoin a miner can add to a block decreases approximately every four years (or precisely every 210,000 blocks). It started at 50 bitcoin per block in January of 2009 and halved to 25 bitcoin per block in November of 2012. It halved again to 12.5 bitcoin in July 2016. Based on this formula, bitcoin mining rewards decrease exponentially until approximately the year 2140, when all bitcoin (20.99999998 million) will have been issued. After 2140, no new bitcoin will be issued.
Bitcoin miners also earn fees from transactions. Every transaction may include a transaction fee, in the form of a surplus of bitcoin between the transaction’s inputs and outputs. The winning bitcoin miner gets to "keep the change" on the transactions included in the winning block. Today, the fees represent 0.5% or less of a bitcoin miner’s income, the vast majority coming from the newly minted bitcoin. However, as the reward decreases over time and the number of transactions per block increases, a greater proportion of bitcoin mining earnings will come from fees. Gradually, the mining reward will be dominated by transaction fees, which will form the primary incentive for miners. After 2140, the amount of new bitcoin in each block drops to zero and bitcoin mining will be incentivized only by transaction fees.
In this chapter, we will first examine mining as a monetary supply mechanism and then look at the most important function of mining: the decentralized consensus mechanism that underpins bitcoin’s security.
To understand mining and consensus, we will follow Alice’s transaction as it is received and added to a block by Jing’s mining equipment. Then we will follow the block as it is mined, added to the blockchain, and accepted by the bitcoin network through the process of emergent consensus.
Bitcoin Economics and Currency Creation
Bitcoin are "minted" during the creation of each block at a fixed and diminishing rate. Each block, generated on average every 10 minutes, contains entirely new bitcoin, created from nothing. Every 210,000 blocks, or approximately every four years, the currency issuance rate is decreased by 50%. For the first four years of operation of the network, each block contained 50 new bitcoin.
In November 2012, the new bitcoin issuance rate was decreased to 25 bitcoin per block. In July of 2016 it was decreased again to 12.5 bitcoin per block. It will halve again to 6.25 bitcoin at block 630,000, which will be mined sometime in 2020. The rate of new coins decreases like this exponentially over 32 "halvings" until block 6,720,000 (mined approximately in year 2137), when it reaches the minimum currency unit of 1 satoshi. Finally, after 6.93 million blocks, in approximately 2140, almost 2,099,999,997,690,000 satoshis, or almost 21 million bitcoin, will be issued. Thereafter, blocks will contain no new bitcoin, and miners will be rewarded solely through the transaction fees. [bitcoin_money_supply] shows the total bitcoin in circulation over time, as the issuance of currency decreases.
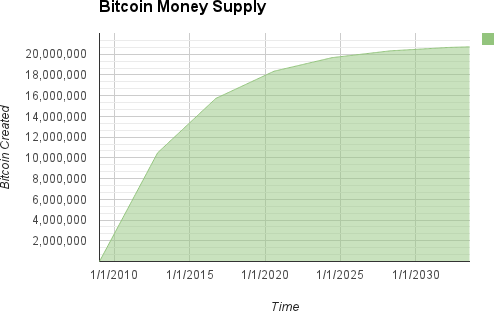
|
Note
|
The maximum number of coins mined is the upper limit of possible mining rewards for bitcoin. In practice, a miner may intentionally mine a block taking less than the full reward. Such blocks have already been mined and more may be mined in the future, resulting in a lower total issuance of the currency. |
In the example code in [max_money], we calculate the total amount of bitcoin that will be issued.
# Original block reward for miners was 50 BTC start_block_reward = 50 # 210000 is around every 4 years with a 10 minute block interval reward_interval = 210000 def max_money(): # 50 BTC = 50 0000 0000 Satoshis current_reward = 50 * 10**8 total = 0 while current_reward > 0: total += reward_interval * current_reward current_reward /= 2 return total print "Total BTC to ever be created:", max_money(), "Satoshis"
[max_money_run] shows the output produced by running this script.
$ python max_money.py Total BTC to ever be created: 2099999997690000 Satoshis
The finite and diminishing issuance creates a fixed monetary supply that resists inflation. Unlike a fiat currency, which can be printed in infinite numbers by a central bank, bitcoin can never be inflated by printing.
Decentralized Consensus
In the previous chapter we looked at the blockchain, the global public ledger (list) of all transactions, which everyone in the bitcoin network accepts as the authoritative record of ownership.
But how can everyone in the network agree on a single universal "truth" about who owns what, without having to trust anyone? All traditional payment systems depend on a trust model that has a central authority providing a clearinghouse service, basically verifying and clearing all transactions. Bitcoin has no central authority, yet somehow every full node has a complete copy of a public ledger that it can trust as the authoritative record. The blockchain is not created by a central authority, but is assembled independently by every node in the network. Somehow, every node in the network, acting on information transmitted across insecure network connections, can arrive at the same conclusion and assemble a copy of the same public ledger as everyone else. This chapter examines the process by which the bitcoin network achieves global consensus without central authority.
Satoshi Nakamoto’s main invention is the decentralized mechanism for emergent consensus. Emergent, because consensus is not achieved explicitly—there is no election or fixed moment when consensus occurs. Instead, consensus is an emergent artifact of the asynchronous interaction of thousands of independent nodes, all following simple rules. All the properties of bitcoin, including currency, transactions, payments, and the security model that does not depend on central authority or trust, derive from this invention.
Bitcoin’s decentralized consensus emerges from the interplay of four processes that occur independently on nodes across the network:
-
Independent verification of each transaction, by every full node, based on a comprehensive list of criteria
-
Independent aggregation of those transactions into new blocks by mining nodes, coupled with demonstrated computation through a Proof-of-Work algorithm
-
Independent verification of the new blocks by every node and assembly into a chain
-
Independent selection, by every node, of the chain with the most cumulative computation demonstrated through Proof-of-Work
In the next few sections we will examine these processes and how they interact to create the emergent property of network-wide consensus that allows any bitcoin node to assemble its own copy of the authoritative, trusted, public, global ledger.
Independent Verification of Transactions
In [transactions], we saw how wallet software creates transactions by collecting UTXO, providing the appropriate unlocking scripts, and then constructing new outputs assigned to a new owner. The resulting transaction is then sent to the neighboring nodes in the bitcoin network so that it can be propagated across the entire bitcoin network.
However, before forwarding transactions to its neighbors, every bitcoin node that receives a transaction will first verify the transaction. This ensures that only valid transactions are propagated across the network, while invalid transactions are discarded at the first node that encounters them.
Each node verifies every transaction against a long checklist of criteria:
-
The transaction’s syntax and data structure must be correct.
-
Neither lists of inputs or outputs are empty.
-
The transaction size in bytes is less than
MAX_BLOCK_SIZE. -
Each output value, as well as the total, must be within the allowed range of values (less than 21m coins, more than the dust threshold).
-
None of the inputs have hash=0, N=–1 (coinbase transactions should not be relayed).
-
nLocktimeis equal toINT_MAX, ornLocktimeandnSequencevalues are satisfied according toMedianTimePast. -
The transaction size in bytes is greater than or equal to 100.
-
The number of signature operations (SIGOPS) contained in the transaction is less than the signature operation limit.
-
The unlocking script (
scriptSig) can only push numbers on the stack, and the locking script (scriptPubkey) must matchisStandardforms (this rejects "nonstandard" transactions). -
A matching transaction in the pool, or in a block in the main branch, must exist.
-
For each input, if the referenced output exists in any other transaction in the pool, the transaction must be rejected.
-
For each input, look in the main branch and the transaction pool to find the referenced output transaction. If the output transaction is missing for any input, this will be an orphan transaction. Add to the orphan transactions pool, if a matching transaction is not already in the pool.
-
For each input, if the referenced output transaction is a coinbase output, it must have at least
COINBASE_MATURITY(100) confirmations. -
For each input, the referenced output must exist and cannot already be spent.
-
Using the referenced output transactions to get input values, check that each input value, as well as the sum, are in the allowed range of values (less than 21m coins, more than 0).
-
Reject if the sum of input values is less than sum of output values.
-
Reject if transaction fee would be too low (
minRelayTxFee) to get into an empty block. -
The unlocking scripts for each input must validate against the corresponding output locking scripts.
These conditions can be seen in detail in the functions AcceptToMemoryPool, CheckTransaction, and CheckInputs in Bitcoin Core. Note that the conditions change over time, to address new types of denial-of-service attacks or sometimes to relax the rules so as to include more types of transactions.
By independently verifying each transaction as it is received and before propagating it, every node builds a pool of valid (but unconfirmed) transactions known as the transaction pool, memory pool, or mempool.
Mining Nodes
Some of the nodes on the bitcoin network are specialized nodes called miners. In [ch01_intro_what_is_bitcoin] we introduced Jing, a computer engineering student in Shanghai, China, who is a bitcoin miner. Jing earns bitcoin by running a "mining rig," which is a specialized computer-hardware system designed to mine bitcoin. Jing’s specialized mining hardware is connected to a server running a full bitcoin node. Unlike Jing, some miners mine without a full node, as we will see in [mining_pools]. Like every other full node, Jing’s node receives and propagates unconfirmed transactions on the bitcoin network. Jing’s node, however, also aggregates these transactions into new blocks.
Jing’s node is listening for new blocks, propagated on the bitcoin network, as do all nodes. However, the arrival of a new block has special significance for a mining node. The competition among miners effectively ends with the propagation of a new block that acts as an announcement of a winner. To miners, receiving a valid new block means someone else won the competition and they lost. However, the end of one round of a competition is also the beginning of the next round. The new block is not just a checkered flag, marking the end of the race; it is also the starting pistol in the race for the next block.
Aggregating Transactions into Blocks
After validating transactions, a bitcoin node will add them to the memory pool, or transaction pool, where transactions await until they can be included (mined) into a block. Jing’s node collects, validates, and relays new transactions just like any other node. Unlike other nodes, however, Jing’s node will then aggregate these transactions into a candidate block.
Let’s follow the blocks that were created during the time Alice bought a cup of coffee from Bob’s Cafe (see [cup_of_coffee]). Alice’s transaction was included in block 277,316. For the purpose of demonstrating the concepts in this chapter, let’s assume that block was mined by Jing’s mining system and follows Alice’s transaction as it becomes part of this new block.
Jing’s mining node maintains a local copy of the blockchain. By the time Alice buys the cup of coffee, Jing’s node has assembled a chain up to block 277,314. Jing’s node is listening for transactions, trying to mine a new block and also listening for blocks discovered by other nodes. As Jing’s node is mining, it receives block 277,315 through the bitcoin network. The arrival of this block signifies the end of the competition for block 277,315 and the beginning of the competition to create block 277,316.
During the previous 10 minutes, while Jing’s node was searching for a solution to block 277,315, it was also collecting transactions in preparation for the next block. By now it has collected a few hundred transactions in the memory pool. Upon receiving block 277,315 and validating it, Jing’s node will also compare it against all the transactions in the memory pool and remove any that were included in block 277,315. Whatever transactions remain in the memory pool are unconfirmed and are waiting to be recorded in a new block.
Jing’s node immediately constructs a new empty block, a candidate for block 277,316. This block is called a candidate block because it is not yet a valid block, as it does not contain a valid Proof-of-Work. The block becomes valid only if the miner succeeds in finding a solution to the Proof-of-Work algorithm.
When Jing’s node aggregates all the transactions from the memory pool, the new candidate block has 418 transactions with total transaction fees of 0.09094928 bitcoin. You can see this block in the blockchain using the Bitcoin Core client command-line interface, as shown in [block277316].
$ bitcoin-cli getblockhash 277316 0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4 $ bitcoin-cli getblock 0000000000000001b6b9a13b095e96db41c4a928b97ef2d9\ 44a9b31b2cc7bdc4
{ "hash" : "0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4", "confirmations" : 35561, "size" : 218629, "height" : 277316, "version" : 2, "merkleroot" : "c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2e", "tx" : [ "d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f", "b268b45c59b39d759614757718b9918caf0ba9d97c56f3b91956ff877c503fbe", ... 417 more transactions ... ], "time" : 1388185914, "nonce" : 924591752, "bits" : "1903a30c", "difficulty" : 1180923195.25802612, "chainwork" : "000000000000000000000000000000000000000000000934695e92aaf53afa1a", "previousblockhash" : "0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569" }
The Coinbase Transaction
The first transaction in any block is a special transaction, called a coinbase transaction. This transaction is constructed by Jing’s node and contains his reward for the mining effort.
|
Note
|
When block 277,316 was mined, the reward was 25 bitcoin per block. Since then, one "halving" period has elapsed. The block reward changed to 12.5 bitcoin in July 2016. It will be halved again in 210,000 blocks, in the year 2020. |
Jing’s node creates the coinbase transaction as a payment to his own wallet: "Pay Jing’s address 25.09094928 bitcoin." The total amount of reward that Jing collects for mining a block is the sum of the coinbase reward (25 new bitcoin) and the transaction fees (0.09094928) from all the transactions included in the block as shown in [generation_tx_example].
$ bitcoin-cli getrawtransaction d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f 1{ "hex" : "01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff0f03443b0403858402062f503253482fffffffff0110c08d9500000000232102aa970c592640d19de03ff6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21ac00000000", "txid" : "d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f", "version" : 1, "locktime" : 0, "vin" : [ { "coinbase" : "03443b0403858402062f503253482f", "sequence" : 4294967295 } ], "vout" : [ { "value" : 25.09094928, "n" : 0, "scriptPubKey" : { "asm" : "02aa970c592640d19de03ff6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21OP_CHECKSIG", "hex" : "2102aa970c592640d19de03ff6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21ac", "reqSigs" : 1, "type" : "pubkey", "addresses" : [ "1MxTkeEP2PmHSMze5tUZ1hAV3YTKu2Gh1N" ] } } ] }
Unlike regular transactions, the coinbase transaction does not consume (spend) UTXO as inputs. Instead, it has only one input, called the coinbase, which creates bitcoin from nothing. The coinbase transaction has one output, payable to the miner’s own bitcoin address. The output of the coinbase transaction sends the value of 25.09094928 bitcoin to the miner’s bitcoin address; in this case it is 1MxTkeEP2PmHSMze5tUZ1hAV3YTKu2Gh1N.
Coinbase Reward and Fees
To construct the coinbase transaction, Jing’s node first calculates the total amount of transaction fees by adding all the inputs and outputs of the 418 transactions that were added to the block. The fees are calculated as:
Total Fees = Sum(Inputs) - Sum(Outputs)In block 277,316, the total transaction fees are 0.09094928 bitcoin.
Next, Jing’s node calculates the correct reward for the new block. The reward is calculated based on the block height, starting at 50 bitcoin per block and reduced by half every 210,000 blocks. Because this block is at height 277,316, the correct reward is 25 bitcoin.
The calculation can be seen in function GetBlockSubsidy in the Bitcoin Core client, as shown in [getblocksubsidy_source].
CAmount GetBlockSubsidy(int nHeight, const Consensus::Params& consensusParams) { int halvings = nHeight / consensusParams.nSubsidyHalvingInterval; // Force block reward to zero when right shift is undefined. if (halvings >= 64) return 0; CAmount nSubsidy = 50 * COIN; // Subsidy is cut in half every 210,000 blocks which will occur approximately every 4 years. nSubsidy >>= halvings; return nSubsidy; }
The initial subsidy is calculated in satoshis by multiplying 50 with the COIN constant (100,000,000 satoshis). This sets the initial reward (nSubsidy) at 5 billion satoshis.
Next, the function calculates the number of halvings that have occurred by dividing the current block height by the halving interval (SubsidyHalvingInterval). In the case of block 277,316, with a halving interval every 210,000 blocks, the result is 1 halving.
The maximum number of halvings allowed is 64, so the code imposes a zero reward (returns only the fees) if the 64 halvings is exceeded.
Next, the function uses the binary-right-shift operator to divide the reward (nSubsidy) by two for each round of halving. In the case of block 277,316, this would binary-right-shift the reward of 5 billion satoshis once (one halving) and result in 2.5 billion satoshis, or 25 bitcoin. The binary-right-shift operator is used because it is more efficient for division by two than integer or floating-point division.
Finally, the coinbase reward (nSubsidy) is added to the transaction fees (nFees), and the sum is returned.
|
Tip
|
If Jing’s mining node writes the coinbase transaction, what stops Jing from "rewarding" himself 100 or 1000 bitcoin? The answer is that an incorrect reward would result in the block being deemed invalid by everyone else, wasting Jing’s electricity used for Proof-of-Work. Jing only gets to spend the reward if the block is accepted by everyone. |
Structure of the Coinbase Transaction
With these calculations, Jing’s node then constructs the coinbase transaction to pay himself 25.09094928 bitcoin.
As you can see in [generation_tx_example], the coinbase transaction has a special format. Instead of a transaction input specifying a previous UTXO to spend, it has a "coinbase" input. We examined transaction inputs in [tx_in_structure]. Let’s compare a regular transaction input with a coinbase transaction input. [table_8-1] shows the structure of a regular transaction, while [table_8-2] shows the structure of the coinbase transaction’s input.
| Size | Field | Description |
|---|---|---|
32 bytes |
Transaction Hash |
Pointer to the transaction containing the UTXO to be spent |
4 bytes |
Output Index |
The index number of the UTXO to be spent, first one is 0 |
1–9 bytes (VarInt) |
Unlocking-Script Size |
Unlocking-Script length in bytes, to follow |
Variable |
Unlocking-Script |
A script that fulfills the conditions of the UTXO locking script |
4 bytes |
Sequence Number |
Currently disabled Tx-replacement feature, set to 0xFFFFFFFF |
| Size | Field | Description |
|---|---|---|
32 bytes |
Transaction Hash |
All bits are zero: Not a transaction hash reference |
4 bytes |
Output Index |
All bits are ones: 0xFFFFFFFF |
1–9 bytes (VarInt) |
Coinbase Data Size |
Length of the coinbase data, from 2 to 100 bytes |
Variable |
Coinbase Data |
Arbitrary data used for extra nonce and mining tags. In v2 blocks; must begin with block height |
4 bytes |
Sequence Number |
Set to 0xFFFFFFFF |
In a coinbase transaction, the first two fields are set to values that do not represent a UTXO reference. Instead of a "transaction hash," the first field is filled with 32 bytes all set to zero. The "output index" is filled with 4 bytes all set to 0xFF (255 decimal). The "Unlocking Script" (scriptSig) is replaced by coinbase data, a data field used by the miners, as we will see next.
Coinbase Data
Coinbase transactions do not have an unlocking script (aka, scriptSig) field. Instead, this field is replaced by coinbase data, which must be between 2 and 100 bytes. Except for the first few bytes, the rest of the coinbase data can be used by miners in any way they want; it is arbitrary data.
In the genesis block, for example, Satoshi Nakamoto added the text "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks" in the coinbase data, using it as a proof of the date and to convey a message. Currently, miners use the coinbase data to include extra nonce values and strings identifying the mining pool.
The first few bytes of the coinbase used to be arbitrary, but that is no longer the case. As per BIP-34, version-2 blocks (blocks with the version field set to 2) must contain the block height index as a script "push" operation in the beginning of the coinbase field.
In block 277,316 we see that the coinbase (see [generation_tx_example]), which is in the unlocking script or scriptSig field of the transaction input, contains the hexadecimal value 03443b0403858402062f503253482f. Let’s decode this value.
The first byte, 03, instructs the script execution engine to push the next three bytes onto the script stack (see [tx_script_ops_table_pushdata]). The next three bytes, 0x443b04, are the block height encoded in little-endian format (backward, least-significant byte first). Reverse the order of the bytes and the result is 0x043b44, which is 277,316 in decimal.
The next few hexadecimal digits (0385840206) are used to encode an extra nonce (see [extra_nonce]), or random value, used to find a suitable Proof-of-Work solution.
The final part of the coinbase data (2f503253482f) is the ASCII-encoded string /P2SH/, which indicates that the mining node that mined this block supports the P2SH improvement defined in BIP-16. The introduction of the P2SH capability required signaling by miners to endorse either BIP-16 or BIP-17. Those endorsing the BIP-16 implementation were to include /P2SH/ in their coinbase data. Those endorsing the BIP-17 implementation of P2SH were to include the string p2sh/CHV in their coinbase data. The BIP-16 was elected as the winner, and many miners continued including the string /P2SH/ in their coinbase to indicate support for this feature.
[satoshi_words] uses the libbitcoin library introduced in [alt_libraries] to extract the coinbase data from the genesis block, displaying Satoshi’s message. Note that the libbitcoin library contains a static copy of the genesis block, so the example code can retrieve the genesis block directly from the library.
/* Display the genesis block message by Satoshi. */ #include <iostream> #include <bitcoin/bitcoin.hpp> int main() { // Create genesis block. const bc::block_type block = bc::genesis_block(); // Genesis block contains a single coinbase transaction. assert(block.transactions.size() == 1); // Get first transaction in block (coinbase). const bc::transaction_type& coinbase_tx = block.transactions[0]; // Coinbase tx has a single input. assert(coinbase_tx.inputs.size() == 1); const bc::transaction_input_type& coinbase_input = coinbase_tx.inputs[0]; // Convert the input script to its raw format. const bc::data_chunk raw_message = save_script(coinbase_input.script); // Convert this to an std::string. std::string message; message.resize(raw_message.size()); std::copy(raw_message.begin(), raw_message.end(), message.begin()); // Display the genesis block message. std::cout << message << std::endl; return 0; }
We compile the code with the GNU C++ compiler and run the resulting executable, as shown in [satoshi_words_run].
$ # Compile the code $ g++ -o satoshi-words satoshi-words.cpp $(pkg-config --cflags --libs libbitcoin) $ # Run the executable $ ./satoshi-words ^D��<GS>^A^DEThe Times 03/Jan/2009 Chancellor on brink of second bailout for banks
Constructing the Block Header
To construct the block header, the mining node needs to fill in six fields, as listed in [block_header_structure_ch10].
| Size | Field | Description |
|---|---|---|
4 bytes |
Version |
A version number to track software/protocol upgrades |
32 bytes |
Previous Block Hash |
A reference to the hash of the previous (parent) block in the chain |
32 bytes |
Merkle Root |
A hash of the root of the merkle tree of this block’s transactions |
4 bytes |
Timestamp |
The approximate creation time of this block (seconds from Unix Epoch) |
4 bytes |
Target |
The Proof-of-Work algorithm target for this block |
4 bytes |
Nonce |
A counter used for the Proof-of-Work algorithm |
At the time that block 277,316 was mined, the version number describing the block structure is version 2, which is encoded in little-endian format in 4 bytes as 0x02000000.
Next, the mining node needs to add the "Previous Block Hash" (also known as prevhash). That is the hash of the block header of block 277,315, the previous block received from the network, which Jing’s node has accepted and selected as the parent of the candidate block 277,316. The block header hash for block 277,315 is:
0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569|
Tip
|
By selecting the specific parent block, indicated by the Previous Block Hash field in the candidate block header, Jing is committing his mining power to extending the chain that ends in that specific block. In essence, this is how Jing "votes" with his mining power for the longest-difficulty valid chain. |
The next step is to summarize all the transactions with a merkle tree, in order to add the merkle root to the block header. The coinbase transaction is listed as the first transaction in the block. Then, 418 more transactions are added after it, for a total of 419 transactions in the block. As we saw in the [merkle_trees], there must be an even number of "leaf" nodes in the tree, so the last transaction is duplicated, creating 420 nodes, each containing the hash of one transaction. The transaction hashes are then combined, in pairs, creating each level of the tree, until all the transactions are summarized into one node at the "root" of the tree. The root of the merkle tree summarizes all the transactions into a single 32-byte value, which you can see listed as "merkle root" in [block277316], and here:
c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2eJing’s mining node will then add a 4-byte timestamp, encoded as a Unix "epoch" timestamp, which is based on the number of seconds elapsed from January 1, 1970, midnight UTC/GMT. The time 1388185914 is equal to Friday, 27 Dec 2013, 23:11:54 UTC/GMT.
Jing’s node then fills in the target, which defines the required Proof-of-Work to make this a valid block. The target is stored in the block as a "target bits" metric, which is a mantissa-exponent encoding of the target. The encoding has a 1-byte exponent, followed by a 3-byte mantissa (coefficient). In block 277,316, for example, the target bits value is 0x1903a30c. The first part 0x19 is a hexadecimal exponent, while the next part, 0x03a30c, is the coefficient. The concept of a target is explained in [target] and the "target bits" representation is explained in [target_bits].
The final field is the nonce, which is initialized to zero.
With all the other fields filled, the block header is now complete and the process of mining can begin. The goal is now to find a value for the nonce that results in a block header hash that is less than the target. The mining node will need to test billions or trillions of nonce values before a nonce is found that satisfies the requirement.
Mining the Block
Now that a candidate block has been constructed by Jing’s node, it is time for Jing’s hardware mining rig to "mine" the block, to find a solution to the Proof-of-Work algorithm that makes the block valid. Throughout this book we have studied cryptographic hash functions as used in various aspects of the bitcoin system. The hash function SHA256 is the function used in bitcoin’s mining process.
In the simplest terms, mining is the process of hashing the block header repeatedly, changing one parameter, until the resulting hash matches a specific target. The hash function’s result cannot be determined in advance, nor can a pattern be created that will produce a specific hash value. This feature of hash functions means that the only way to produce a hash result matching a specific target is to try again and again, randomly modifying the input until the desired hash result appears by chance.
Proof-of-Work Algorithm
A hash algorithm takes an arbitrary-length data input and produces a fixed-length deterministic result, a digital fingerprint of the input. For any specific input, the resulting hash will always be the same and can be easily calculated and verified by anyone implementing the same hash algorithm. The key characteristic of a cryptographic hash algorithm is that it is computationally infeasible to find two different inputs that produce the same fingerprint (known as a collision). As a corollary, it is also virtually impossible to select an input in such a way as to produce a desired fingerprint, other than trying random inputs.
With SHA256, the output is always 256 bits long, regardless of the size of the input. In [sha256_example1], we will use the Python interpreter to calculate the SHA256 hash of the phrase, "I am Satoshi Nakamoto."
$ python
[sha256_example1] shows the result of calculating the hash of "I am Satoshi Nakamoto": 5d7c7ba21cbbcd75d14800b100252d5b428e5b1213d27c385bc141ca6b47989e. This 256-bit number is the hash or digest of the phrase and depends on every part of the phrase. Adding a single letter, punctuation mark, or any other character will produce a different hash.
Now, if we change the phrase, we should expect to see completely different hashes. Let’s try that by adding a number to the end of our phrase, using the simple Python scripting in [sha256_example_generator].
# example of iterating a nonce in a hashing algorithm's input import hashlib text = "I am Satoshi Nakamoto" # iterate nonce from 0 to 19 for nonce in xrange(20): # add the nonce to the end of the text input = text + str(nonce) # calculate the SHA-256 hash of the input (text+nonce) hash = hashlib.sha256(input).hexdigest() # show the input and hash result print input, '=>', hash
Running this will produce the hashes of several phrases, made different by adding a number at the end of the text. By incrementing the number, we can get different hashes, as shown in [sha256_example_generator_output].
$ python hash_example.pyI am Satoshi Nakamoto0 => a80a81401765c8eddee25df36728d732...
I am Satoshi Nakamoto1 => f7bc9a6304a4647bb41241a677b5345f...
I am Satoshi Nakamoto2 => ea758a8134b115298a1583ffb80ae629...
I am Satoshi Nakamoto3 => bfa9779618ff072c903d773de30c99bd...
I am Satoshi Nakamoto4 => bce8564de9a83c18c31944a66bde992f...
I am Satoshi Nakamoto5 => eb362c3cf3479be0a97a20163589038e...
I am Satoshi Nakamoto6 => 4a2fd48e3be420d0d28e202360cfbaba...
I am Satoshi Nakamoto7 => 790b5a1349a5f2b909bf74d0d166b17a...
I am Satoshi Nakamoto8 => 702c45e5b15aa54b625d68dd947f1597...
I am Satoshi Nakamoto9 => 7007cf7dd40f5e933cd89fff5b791ff0...
I am Satoshi Nakamoto10 => c2f38c81992f4614206a21537bd634a...
I am Satoshi Nakamoto11 => 7045da6ed8a914690f087690e1e8d66...
I am Satoshi Nakamoto12 => 60f01db30c1a0d4cbce2b4b22e88b9b...
I am Satoshi Nakamoto13 => 0ebc56d59a34f5082aaef3d66b37a66...
I am Satoshi Nakamoto14 => 27ead1ca85da66981fd9da01a8c6816...
I am Satoshi Nakamoto15 => 394809fb809c5f83ce97ab554a2812c...
I am Satoshi Nakamoto16 => 8fa4992219df33f50834465d3047429...
I am Satoshi Nakamoto17 => dca9b8b4f8d8e1521fa4eaa46f4f0cd...
I am Satoshi Nakamoto18 => 9989a401b2a3a318b01e9ca9a22b0f3...
I am Satoshi Nakamoto19 => cda56022ecb5b67b2bc93a2d764e75f...Each phrase produces a completely different hash result. They seem completely random, but you can reproduce the exact results in this example on any computer with Python and see the same exact hashes.
The number used as a variable in such a scenario is called a nonce. The nonce is used to vary the output of a cryptographic function, in this case to vary the SHA256 fingerprint of the phrase.
To make a challenge out of this algorithm, let’s set a target: find a phrase that produces a hexadecimal hash that starts with a zero. Fortunately, this isn’t difficult! [sha256_example_generator_output] shows that the phrase "I am Satoshi Nakamoto13" produces the hash 0ebc56d59a34f5082aaef3d66b37a661696c2b618e62432727216ba9531041a5, which fits our criteria. It took 13 attempts to find it. In terms of probabilities, if the output of the hash function is evenly distributed we would expect to find a result with a 0 as the hexadecimal prefix once every 16 hashes (one out of 16 hexadecimal digits 0 through F). In numerical terms, that means finding a hash value that is less than 0x1000000000000000000000000000000000000000000000000000000000000000. We call this threshold the target and the goal is to find a hash that is numerically less than the target. If we decrease the target, the task of finding a hash that is less than the target becomes more and more difficult.
To give a simple analogy, imagine a game where players throw a pair of dice repeatedly, trying to throw less than a specified target. In the first round, the target is 12. Unless you throw double-six, you win. In the next round the target is 11. Players must throw 10 or less to win, again an easy task. Let’s say a few rounds later the target is down to 5. Now, more than half the dice throws will exceed the target and therefore be invalid. It takes exponentially more dice throws to win, the lower the target gets. Eventually, when the target is 2 (the minimum possible), only one throw out of every 36, or 2% of them, will produce a winning result.
From the perspective of an observer who knows that the target of the dice game is 2, if someone has succeeded in casting a winning throw it can be assumed that they attempted, on average, 36 throws. In other words, one can estimate the amount of work it takes to succeed from the difficulty imposed by the target. When the algorithm is a based on a deterministic function such as SHA256, the input itself constitutes proof that a certain amount of work was done to produce a result below the target. Hence, Proof-of-Work.
|
Tip
|
Even though each attempt produces a random outcome, the probability of any possible outcome can be calculated in advance. Therefore, an outcome of specified difficulty constitutes proof of a specific amount of work. |
In [sha256_example_generator_output], the winning "nonce" is 13 and this result can be confirmed by anyone independently. Anyone can add the number 13 as a suffix to the phrase "I am Satoshi Nakamoto" and compute the hash, verifying that it is less than the target. The successful result is also Proof-of-Work, because it proves we did the work to find that nonce. While it only takes one hash computation to verify, it took us 13 hash computations to find a nonce that worked. If we had a lower target (higher difficulty) it would take many more hash computations to find a suitable nonce, but only one hash computation for anyone to verify. Furthermore, by knowing the target, anyone can estimate the difficulty using statistics and therefore know how much work was needed to find such a nonce.
|
Tip
|
The Proof-of-Work must produce a hash that is less than the target. A higher target means it is less difficult to find a hash that is below the target. A lower target means it is more difficult to find a hash below the target. The target and difficulty are inversely related. |
Bitcoin’s Proof-of-Work is very similar to the challenge shown in [sha256_example_generator_output]. The miner constructs a candidate block filled with transactions. Next, the miner calculates the hash of this block’s header and sees if it is smaller than the current target. If the hash is not less than the target, the miner will modify the nonce (usually just incrementing it by one) and try again. At the current difficulty in the bitcoin network, miners have to try quadrillions of times before finding a nonce that results in a low enough block header hash.
A very simplified Proof-of-Work algorithm is implemented in Python in [pow_example1].
#!/usr/bin/env python # example of proof-of-work algorithm import hashlib import time max_nonce = 2 ** 32 # 4 billion def proof_of_work(header, difficulty_bits): # calculate the difficulty target target = 2 ** (256-difficulty_bits) for nonce in xrange(max_nonce): hash_result = hashlib.sha256(str(header)+str(nonce)).hexdigest() # check if this is a valid result, below the target if long(hash_result, 16) < target: print "Success with nonce %d" % nonce print "Hash is %s" % hash_result return (hash_result,nonce) print "Failed after %d (max_nonce) tries" % nonce return nonce if __name__ == '__main__': nonce = 0 hash_result = '' # difficulty from 0 to 31 bits for difficulty_bits in xrange(32): difficulty = 2 ** difficulty_bits print "Difficulty: %ld (%d bits)" % (difficulty, difficulty_bits) print "Starting search..." # checkpoint the current time start_time = time.time() # make a new block which includes the hash from the previous block # we fake a block of transactions - just a string new_block = 'test block with transactions' + hash_result # find a valid nonce for the new block (hash_result, nonce) = proof_of_work(new_block, difficulty_bits) # checkpoint how long it took to find a result end_time = time.time() elapsed_time = end_time - start_time print "Elapsed Time: %.4f seconds" % elapsed_time if elapsed_time > 0: # estimate the hashes per second hash_power = float(long(nonce)/elapsed_time) print "Hashing Power: %ld hashes per second" % hash_power
Running this code, you can set the desired difficulty (in bits, how many of the leading bits must be zero) and see how long it takes for your computer to find a solution. In [pow_example_outputs], you can see how it works on an average laptop.
$ python proof-of-work-example.py*
Difficulty: 1 (0 bits)
[...]
Difficulty: 8 (3 bits)
Starting search...
Success with nonce 9
Hash is 1c1c105e65b47142f028a8f93ddf3dabb9260491bc64474738133ce5256cb3c1
Elapsed Time: 0.0004 seconds
Hashing Power: 25065 hashes per second
Difficulty: 16 (4 bits)
Starting search...
Success with nonce 25
Hash is 0f7becfd3bcd1a82e06663c97176add89e7cae0268de46f94e7e11bc3863e148
Elapsed Time: 0.0005 seconds
Hashing Power: 52507 hashes per second
Difficulty: 32 (5 bits)
Starting search...
Success with nonce 36
Hash is 029ae6e5004302a120630adcbb808452346ab1cf0b94c5189ba8bac1d47e7903
Elapsed Time: 0.0006 seconds
Hashing Power: 58164 hashes per second
[...]
Difficulty: 4194304 (22 bits)
Starting search...
Success with nonce 1759164
Hash is 0000008bb8f0e731f0496b8e530da984e85fb3cd2bd81882fe8ba3610b6cefc3
Elapsed Time: 13.3201 seconds
Hashing Power: 132068 hashes per second
Difficulty: 8388608 (23 bits)
Starting search...
Success with nonce 14214729
Hash is 000001408cf12dbd20fcba6372a223e098d58786c6ff93488a9f74f5df4df0a3
Elapsed Time: 110.1507 seconds
Hashing Power: 129048 hashes per second
Difficulty: 16777216 (24 bits)
Starting search...
Success with nonce 24586379
Hash is 0000002c3d6b370fccd699708d1b7cb4a94388595171366b944d68b2acce8b95
Elapsed Time: 195.2991 seconds
Hashing Power: 125890 hashes per second
[...]
Difficulty: 67108864 (26 bits)
Starting search...
Success with nonce 84561291
Hash is 0000001f0ea21e676b6dde5ad429b9d131a9f2b000802ab2f169cbca22b1e21a
Elapsed Time: 665.0949 seconds
Hashing Power: 127141 hashes per secondAs you can see, increasing the difficulty by 1 bit causes a doubling in the time it takes to find a solution. If you think of the entire 256-bit number space, each time you constrain one more bit to zero, you decrease the search space by half. In [pow_example_outputs], it takes 84 million hash attempts to find a nonce that produces a hash with 26 leading bits as zero. Even at a speed of more than 120,000 hashes per second, it still requires 10 minutes on a laptop to find this solution.
At the time of writing, the network is attempting to find a block whose header hash is less than:
0000000000000000029AB9000000000000000000000000000000000000000000As you can see, there are a lot of zeros at the beginning of that target, meaning that the acceptable range of hashes is much smaller, hence it’s more difficult to find a valid hash. It will take on average more than 1.8 septa-hashes (thousand billion billion hashes) per second for the network to discover the next block. That seems like an impossible task, but fortunately the network is bringing 3 exa-hashes per second (EH/sec) of processing power to bear, which will be able to find a block in about 10 minutes on average.
Target Representation
In [block277316], we saw that the block contains the target, in a notation called "target bits" or just "bits," which in block 277,316 has the value of 0x1903a30c. This notation expresses the Proof-of-Work target as a coefficient/exponent format, with the first two hexadecimal digits for the exponent and the next six hex digits as the coefficient. In this block, therefore, the exponent is 0x19 and the coefficient is 0x03a30c.
The formula to calculate the difficulty target from this representation is:
target = coefficient * 2^(8 * (exponent – 3))Using that formula, and the difficulty bits value 0x1903a30c, we get:
target = 0x03a30c * 2^(0x08 * (0x19 - 0x03))^
=> target = 0x03a30c * 2^(0x08 * 0x16)^
=> target = 0x03a30c * 2^0xB0^which in decimal is:
=> target = 238,348 * 2^176^
=> target = 22,829,202,948,393,929,850,749,706,076,701,368,331,072,452,018,388,575,715,328switching back to hexadecimal:
=> target = 0x0000000000000003A30C00000000000000000000000000000000000000000000This means that a valid block for height 277,316 is one that has a block header hash that is less than the target. In binary that number must have more than 60 leading bits set to zero. With this level of difficulty, a single miner processing 1 trillion hashes per second (1 terahash per second or 1 TH/sec) would only find a solution once every 8,496 blocks or once every 59 days, on average.
Retargeting to Adjust Difficulty
As we saw, the target determines the difficulty and therefore affects how long it takes to find a solution to the Proof-of-Work algorithm. This leads to the obvious questions: Why is the difficulty adjustable, who adjusts it, and how?
Bitcoin’s blocks are generated every 10 minutes, on average. This is bitcoin’s heartbeat and underpins the frequency of currency issuance and the speed of transaction settlement. It has to remain constant not just over the short term, but over a period of many decades. Over this time, it is expected that computer power will continue to increase at a rapid pace. Furthermore, the number of participants in mining and the computers they use will also constantly change. To keep the block generation time at 10 minutes, the difficulty of mining must be adjusted to account for these changes. In fact, the Proof-of-Work target is a dynamic parameter that is periodically adjusted to meet a 10-minute block interval goal. In simple terms, the target is set so that the current mining power will result in a 10-minute block interval.
How, then, is such an adjustment made in a completely decentralized network? Retargeting occurs automatically and on every node independently. Every 2,016 blocks, all nodes retarget the Proof-of-Work. The equation for retargeting measures the time it took to find the last 2,016 blocks and compares that to the expected time of 20,160 minutes (2,016 blocks times the desired 10-minute block interval). The ratio between the actual timespan and desired timespan is calculated and a proportionate adjustment (up or down) is made to the target. In simple terms: If the network is finding blocks faster than every 10 minutes, the difficulty increases (target decreases). If block discovery is slower than expected, the difficulty decreases (target increases).
The equation can be summarized as:
New Target = Old Target * (Actual Time of Last 2016 Blocks / 20160 minutes)[retarget_code] shows the code used in the Bitcoin Core client.
// Limit adjustment step int64_t nActualTimespan = pindexLast->GetBlockTime() - nFirstBlockTime; LogPrintf(" nActualTimespan = %d before bounds\n", nActualTimespan); if (nActualTimespan < params.nPowTargetTimespan/4) nActualTimespan = params.nPowTargetTimespan/4; if (nActualTimespan > params.nPowTargetTimespan*4) nActualTimespan = params.nPowTargetTimespan*4; // Retarget const arith_uint256 bnPowLimit = UintToArith256(params.powLimit); arith_uint256 bnNew; arith_uint256 bnOld; bnNew.SetCompact(pindexLast->nBits); bnOld = bnNew; bnNew *= nActualTimespan; bnNew /= params.nPowTargetTimespan; if (bnNew > bnPowLimit) bnNew = bnPowLimit;
|
Note
|
While the target calibration happens every 2,016 blocks, because of an off-by-one error in the original Bitcoin Core client it is based on the total time of the previous 2,015 blocks (not 2,016 as it should be), resulting in a retargeting bias toward higher difficulty by 0.05%. |
The parameters Interval (2,016 blocks) and TargetTimespan (two weeks as 1,209,600 seconds) are defined in chainparams.cpp.
To avoid extreme volatility in the difficulty, the retargeting adjustment must be less than a factor of four (4) per cycle. If the required target adjustment is greater than a factor of four, it will be adjusted by a factor of 4 and not more. Any further adjustment will be accomplished in the next retargeting period because the imbalance will persist through the next 2,016 blocks. Therefore, large discrepancies between hashing power and difficulty might take several 2,016 block cycles to balance out.
|
Tip
|
The difficulty of mining a bitcoin block is approximately 10 minutes of processing for the entire network, based on the time it took to mine the previous 2,016 blocks, adjusted every 2,016 blocks. This is achieved by lowering or raising the target. |
Note that the target is independent of the number of transactions or the value of transactions. This means that the amount of hashing power and therefore electricity expended to secure bitcoin is also entirely independent of the number of transactions. Bitcoin can scale up, achieve broader adoption, and remain secure without any increase in hashing power from today’s level. The increase in hashing power represents market forces as new miners enter the market to compete for the reward. As long as enough hashing power is under the control of miners acting honestly in pursuit of the reward, it is enough to prevent "takeover" attacks and, therefore, it is enough to secure bitcoin.
The difficulty of mining is closely related to the cost of electricity and the exchange rate of bitcoin vis-a-vis the currency used to pay for electricity. High-performance mining systems are about as efficient as possible with the current generation of silicon fabrication, converting electricity into hashing computation at the highest rate possible. The primary influence on the mining market is the price of one kilowatt-hour of electricity in bitcoin, because that determines the profitability of mining and therefore the incentives to enter or exit the mining market.
Successfully Mining the Block
As we saw earlier, Jing’s node has constructed a candidate block and prepared it for mining. Jing has several hardware mining rigs with application-specific integrated circuits, where hundreds of thousands of integrated circuits run the SHA256 algorithm in parallel at incredible speeds. Many of these specialized machines are connected to his mining node over USB or a local area network. Next, the mining node running on Jing’s desktop transmits the block header to his mining hardware, which starts testing trillions of nonces per second.
Almost 11 minutes after starting to mine block 277,316, one of the hardware mining machines finds a solution and sends it back to the mining node. When inserted into the block header, the nonce 4,215,469,401 produces a block hash of:
0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569which is less than the target:
0000000000000003A30C00000000000000000000000000000000000000000000Immediately, Jing’s mining node transmits the block to all its peers. They receive, validate, and then propagate the new block. As the block ripples out across the network, each node adds it to its own copy of the blockchain, extending it to a new height of 277,316 blocks. As mining nodes receive and validate the block, they abandon their efforts to find a block at the same height and immediately start computing the next block in the chain, using Jing’s block as the "parent." By building on top of Jing’s newly discovered block, the other miners are essentially "voting" with their mining power and endorsing Jing’s block and the chain it extends.
In the next section, we’ll look at the process each node uses to validate a block and select the longest chain, creating the consensus that forms the decentralized blockchain.
Validating a New Block
The third step in bitcoin’s consensus mechanism is independent validation of each new block by every node on the network. As the newly solved block moves across the network, each node performs a series of tests to validate it before propagating it to its peers. This ensures that only valid blocks are propagated on the network. The independent validation also ensures that miners who act honestly get their blocks incorporated in the blockchain, thus earning the reward. Those miners who act dishonestly have their blocks rejected and not only lose the reward, but also waste the effort expended to find a Proof-of-Work solution, thus incurring the cost of electricity without compensation.
When a node receives a new block, it will validate the block by checking it against a long list of criteria that must all be met; otherwise, the block is rejected. These criteria can be seen in the Bitcoin Core client in the functions CheckBlock and CheckBlockHeader and include:
-
The block data structure is syntactically valid
-
The block header hash is less than the target (enforces the Proof-of-Work)
-
The block timestamp is less than two hours in the future (allowing for time errors)
-
The block size is within acceptable limits
-
The first transaction (and only the first) is a coinbase transaction
-
All transactions within the block are valid using the transaction checklist discussed in [tx_verification]
The independent validation of each new block by every node on the network ensures that the miners cannot cheat. In previous sections we saw how miners get to write a transaction that awards them the new bitcoin created within the block and claim the transaction fees. Why don’t miners write themselves a transaction for a thousand bitcoin instead of the correct reward? Because every node validates blocks according to the same rules. An invalid coinbase transaction would make the entire block invalid, which would result in the block being rejected and, therefore, that transaction would never become part of the ledger. The miners have to construct a perfect block, based on the shared rules that all nodes follow, and mine it with a correct solution to the Proof-of-Work. To do so, they expend a lot of electricity in mining, and if they cheat, all the electricity and effort is wasted. This is why independent validation is a key component of decentralized consensus.
Assembling and Selecting Chains of Blocks
The final step in bitcoin’s decentralized consensus mechanism is the assembly of blocks into chains and the selection of the chain with the most Proof-of-Work. Once a node has validated a new block, it will then attempt to assemble a chain by connecting the block to the existing blockchain.
Nodes maintain three sets of blocks: those connected to the main blockchain, those that form branches off the main blockchain (secondary chains), and finally, blocks that do not have a known parent in the known chains (orphans). Invalid blocks are rejected as soon as any one of the validation criteria fails and are therefore not included in any chain.
The "main chain" at any time is whichever valid chain of blocks has the most cumulative Proof-of-Work associated with it. Under most circumstances this is also the chain with the most blocks in it, unless there are two equal-length chains and one has more Proof-of-Work. The main chain will also have branches with blocks that are "siblings" to the blocks on the main chain. These blocks are valid but not part of the main chain. They are kept for future reference, in case one of those chains is extended to exceed the main chain in work. In the next section ([forks]), we will see how secondary chains occur as a result of an almost simultaneous mining of blocks at the same height.
When a new block is received, a node will try to slot it into the existing blockchain. The node will look at the block’s "previous block hash" field, which is the reference to the block’s parent. Then, the node will attempt to find that parent in the existing blockchain. Most of the time, the parent will be the "tip" of the main chain, meaning this new block extends the main chain. For example, the new block 277,316 has a reference to the hash of its parent block 277,315. Most nodes that receive 277,316 will already have block 277,315 as the tip of their main chain and will therefore link the new block and extend that chain.
Sometimes, as we will see in [forks], the new block extends a chain that is not the main chain. In that case, the node will attach the new block to the secondary chain it extends and then compare the work of the secondary chain to the main chain. If the secondary chain has more cumulative work than the main chain, the node will reconverge on the secondary chain, meaning it will select the secondary chain as its new main chain, making the old main chain a secondary chain. If the node is a miner, it will now construct a block extending this new, longer, chain.
If a valid block is received and no parent is found in the existing chains, that block is considered an "orphan." Orphan blocks are saved in the orphan block pool where they will stay until their parent is received. Once the parent is received and linked into the existing chains, the orphan can be pulled out of the orphan pool and linked to the parent, making it part of a chain. Orphan blocks usually occur when two blocks that were mined within a short time of each other are received in reverse order (child before parent).
By selecting the greatest-cumulative-work valid chain, all nodes eventually achieve network-wide consensus. Temporary discrepancies between chains are resolved eventually as more work is added, extending one of the possible chains. Mining nodes "vote" with their mining power by choosing which chain to extend by mining the next block. When they mine a new block and extend the chain, the new block itself represents their vote.
In the next section we will look at how discrepancies between competing chains (forks) are resolved by the independent selection of the greatest-cumulative-work chain.
Blockchain Forks
Because the blockchain is a decentralized data structure, different copies of it are not always consistent. Blocks might arrive at different nodes at different times, causing the nodes to have different perspectives of the blockchain. To resolve this, each node always selects and attempts to extend the chain of blocks that represents the most Proof-of-Work, also known as the longest chain or greatest cumulative work chain. By summing the work recorded in each block in a chain, a node can calculate the total amount of work that has been expended to create that chain. As long as all nodes select the greatest-cumulative-work chain, the global bitcoin network eventually converges to a consistent state. Forks occur as temporary inconsistencies between versions of the blockchain, which are resolved by eventual reconvergence as more blocks are added to one of the forks.
|
Tip
|
The blockchain forks described in this section occur naturally as a result of transmission delays in the global network. We will also look at deliberately induced forks later in this chapter. |
In the next few diagrams, we follow the progress of a "fork" event across the network. The diagram is a simplified representation of the bitcoin network. For illustration purposes, different blocks are shown as different shapes (star, triangle, upside-down triangle, rhombus), spreading across the network. Each node in the network is represented as a circle.
Each node has its own perspective of the global blockchain. As each node receives blocks from its neighbors, it updates its own copy of the blockchain, selecting the greatest-cumulative-work chain. For illustration purposes, each node contains a shape that represents the block that it believes is currently the tip of the main chain. So, if you see a star shape in the node, that means that the star block is the tip of the main chain, as far as that node is concerned.
In the first diagram ([fork1]), the network has a unified perspective of the blockchain, with the star block as the tip of the main chain.
A "fork" occurs whenever there are two candidate blocks competing to form the longest blockchain. This occurs under normal conditions whenever two miners solve the Proof-of-Work algorithm within a short period of time from each other. As both miners discover a solution for their respective candidate blocks, they immediately broadcast their own "winning" block to their immediate neighbors who begin propagating the block across the network. Each node that receives a valid block will incorporate it into its blockchain, extending the blockchain by one block. If that node later sees another candidate block extending the same parent, it connects the second candidate on a secondary chain. As a result, some nodes will "see" one candidate block first, while other nodes will see the other candidate block and two competing versions of the blockchain will emerge.
In [fork2], we see two miners (Node A and Node B) who mine two different blocks almost simultaneously. Both of these blocks are children of the star block, and extend the chain by building on top of the star block. To help us track it, one is visualized as a triangle block originating from Node A, and the other is shown as an upside-down triangle block originating from Node B.
Let’s assume, for example, that a miner Node A finds a Proof-of-Work solution for a block "triangle" that extends the blockchain, building on top of the parent block "star." Almost simultaneously, the miner Node B who was also extending the chain from block "star" finds a solution for block "upside-down triangle," his candidate block. Now, there are two possible blocks; one we call "triangle," originating in Node A; and one we call "upside-down triangle," originating in Node B. Both blocks are valid, both blocks contain a valid solution to the Proof-of-Work, and both blocks extend the same parent (block "star"). Both blocks likely contain most of the same transactions, with only perhaps a few differences in the order of transactions.
As the two blocks propagate, some nodes receive block "triangle" first and some receive block "upside-down triangle" first. As shown in [fork3], the network splits into two different perspectives of the blockchain; one side topped with a triangle block, the other with the upside-down-triangle block.
In the diagram, a randomly chosen "Node X" received the triangle block first and extended the star chain with it. Node X selected the chain with "triangle" block as the main chain. Later, Node X also received the "upside-down triangle" block. Since it was received second, it is assumed to have "lost" the race. Yet, the "upside-down triangle" block is not discarded. It is linked to the "star" block parent and forms a secondary chain. While Node X assumes it has correctly selected the winning chain, it keeps the "losing" chain so that it has the information needed to reconverge if the "losing" chain ends up "winning."
On the other side of the network, Node Y constructs a blockchain based on its own perspective of the sequence of events. It received "upside-down triangle" first and elected that chain as the "winner." When it later received "triangle" block, it connected it to the "star" block parent as a secondary chain.
Neither side is "correct," or "incorrect." Both are valid perspectives of the blockchain. Only in hindsight will one prevail, based on how these two competing chains are extended by additional work.
Mining nodes whose perspective resembles Node X will immediately begin mining a candidate block that extends the chain with "triangle" as its tip. By linking "triangle" as the parent of their candidate block, they are voting with their hashing power. Their vote supports the chain that they have elected as the main chain.
Any mining node whose perspective resembles Node Y will start building a candidate node with "upside-down triangle" as its parent, extending the chain that they believe is the main chain. And so, the race begins again.
Forks are almost always resolved within one block. While part of the network’s hashing power is dedicated to building on top of "triangle" as the parent, another part of the hashing power is focused on building on top of "upside-down triangle." Even if the hashing power is almost evenly split, it is likely that one set of miners will find a solution and propagate it before the other set of miners have found any solutions. Let’s say, for example, that the miners building on top of "triangle" find a new block "rhombus" that extends the chain (e.g., star-triangle-rhombus). They immediately propagate this new block and the entire network sees it as a valid solution as shown in [fork4].
All nodes that had chosen "triangle" as the winner in the previous round will simply extend the chain one more block. The nodes that chose "upside-down triangle" as the winner, however, will now see two chains: star-triangle-rhombus and star-upside-down-triangle. The chain star-triangle-rhombus is now longer (more cumulative work) than the other chain. As a result, those nodes will set the chain star-triangle-rhombus as the main chain and change the star-upside-down-triangle chain to a secondary chain, as shown in [fork5]. This is a chain reconvergence, because those nodes are forced to revise their view of the blockchain to incorporate the new evidence of a longer chain. Any miners working on extending the chain star-upside-down-triangle will now stop that work because their candidate block is an "orphan," as its parent "upside-down-triangle" is no longer on the longest chain. The transactions within "upside-down-triangle" are re-inserted in the mempool for inclusion in the next block, because the block they were in is no longer in the main chain. The entire network reconverges on a single blockchain star-triangle-rhombus, with "rhombus" as the last block in the chain. All miners immediately start working on candidate blocks that reference "rhombus" as their parent to extend the star-triangle-rhombus chain.
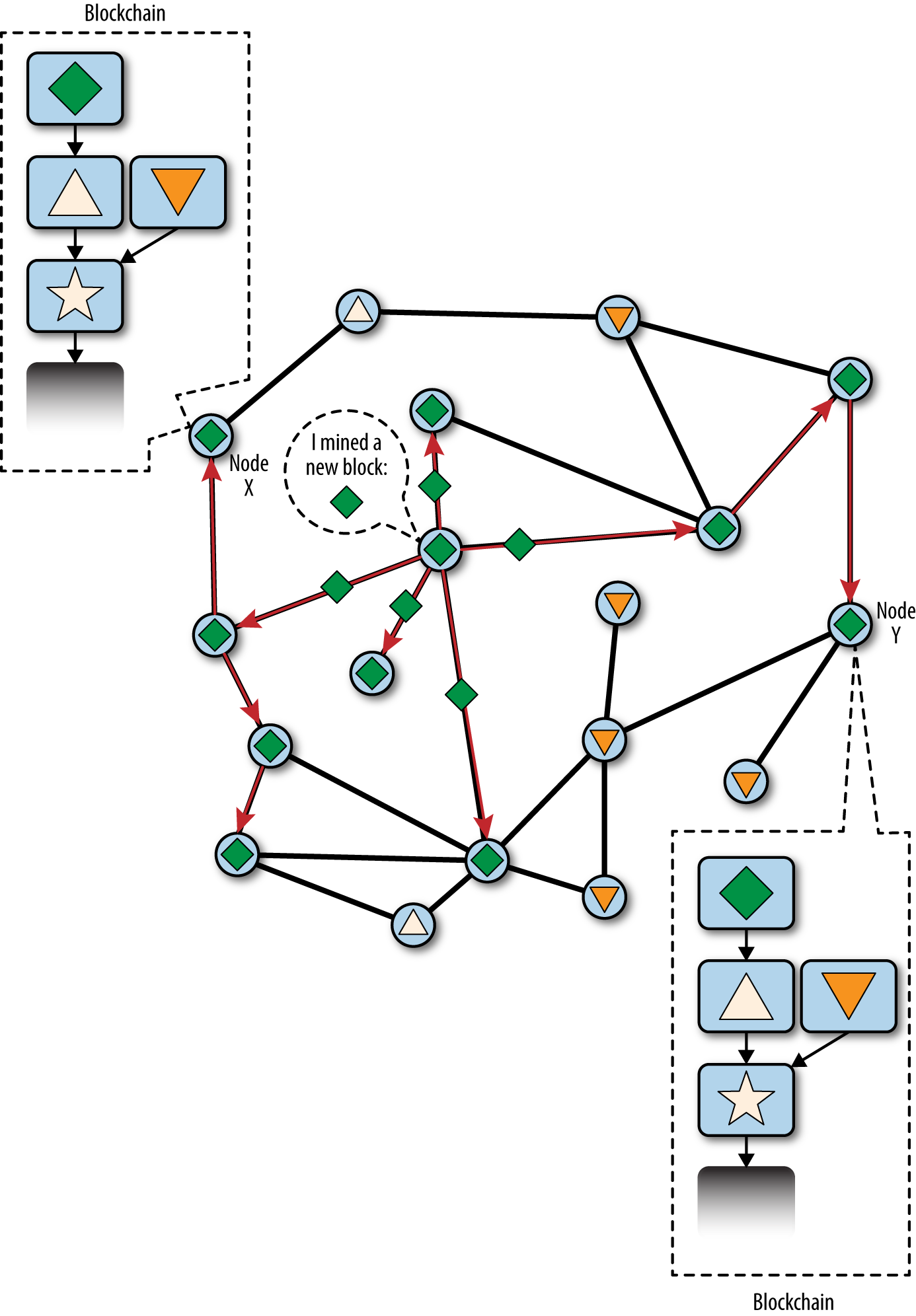
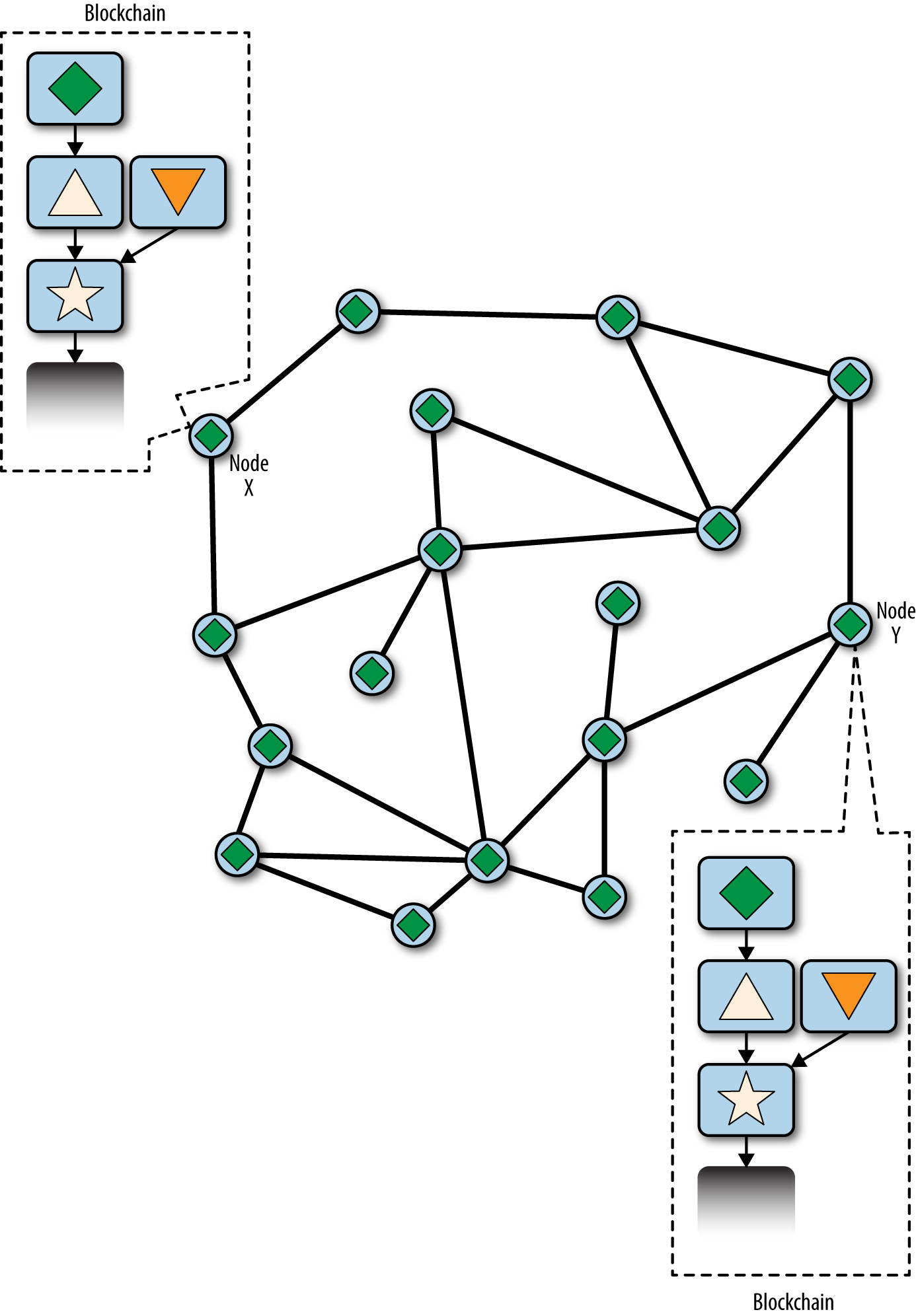
It is theoretically possible for a fork to extend to two blocks, if two blocks are found almost simultaneously by miners on opposite "sides" of a previous fork. However, the chance of that happening is very low. Whereas a one-block fork might occur every day, a two-block fork occurs at most once every few weeks.
Bitcoin’s block interval of 10 minutes is a design compromise between fast confirmation times (settlement of transactions) and the probability of a fork. A faster block time would make transactions clear faster but lead to more frequent blockchain forks, whereas a slower block time would decrease the number of forks but make settlement slower.
Mining and the Hashing Race
Bitcoin mining is an extremely competitive industry. The hashing power has increased exponentially every year of bitcoin’s existence. Some years the growth has reflected a complete change of technology, such as in 2010 and 2011 when many miners switched from using CPU mining to GPU mining and field programmable gate array (FPGA) mining. In 2013 the introduction of ASIC mining lead to another giant leap in mining power, by placing the SHA256 function directly on silicon chips specialized for the purpose of mining. The first such chips could deliver more mining power in a single box than the entire bitcoin network in 2010.
The following list shows the total hashing power of the bitcoin network, over the first five years of operation:
- 2009
-
0.5 MH/sec–8 MH/sec (16× growth)
- 2010
-
8 MH/sec–116 GH/sec (14,500× growth)
- 2011
-
16 GH/sec–9 TH/sec (562× growth)
- 2012
-
9 TH/sec–23 TH/sec (2.5× growth)
- 2013
-
23 TH/sec–10 PH/sec (450× growth)
- 2014
-
10 PH/sec–300 PH/sec (3000× growth)
- 2015
-
300 PH/sec-800 PH/sec (266× growth)
- 2016
-
800 PH/sec-2.5 EH/sec (312× growth))
In the chart in [network_hashing_power], we can see that bitcoin network’s hashing power increased over the past two years. As you can see, the competition between miners and the growth of bitcoin has resulted in an exponential increase in the hashing power (total hashes per second across the network).
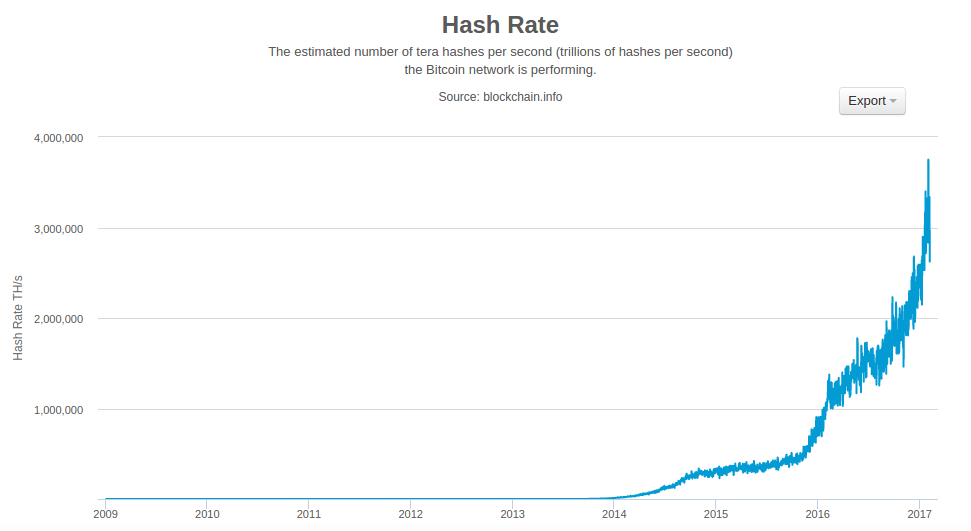
As the amount of hashing power applied to mining bitcoin has exploded, the difficulty has risen to match it. The difficulty metric in the chart shown in [bitcoin_difficulty] is measured as a ratio of current difficulty over minimum difficulty (the difficulty of the first block).
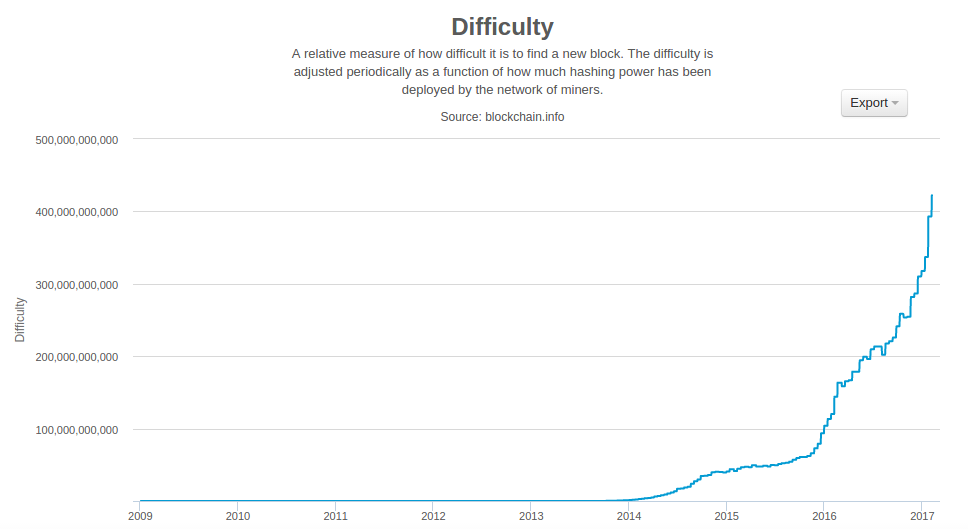
In the last two years, the ASIC mining chips have become increasingly denser, approaching the cutting edge of silicon fabrication with a feature size (resolution) of 16 nanometers (nm). Currently, ASIC manufacturers are aiming to overtake general-purpose CPU chip manufacturers, designing chips with a feature size of 14 nm, because the profitability of mining is driving this industry even faster than general computing. There are no more giant leaps left in bitcoin mining, because the industry has reached the forefront of Moore’s Law, which stipulates that computing density will double approximately every 18 months. Still, the mining power of the network continues to advance at an exponential pace as the race for higher density chips is matched with a race for higher density data centers where thousands of these chips can be deployed. It’s no longer about how much mining can be done with one chip, but how many chips can be squeezed into a building, while still dissipating the heat and providing adequate power.
The Extra Nonce Solution
Since 2012, bitcoin mining has evolved to resolve a fundamental limitation in the structure of the block header. In the early days of bitcoin, a miner could find a block by iterating through the nonce until the resulting hash was below the target. As difficulty increased, miners often cycled through all 4 billion values of the nonce without finding a block. However, this was easily resolved by updating the block timestamp to account for the elapsed time. Because the timestamp is part of the header, the change would allow miners to iterate through the values of the nonce again with different results. Once mining hardware exceeded 4 GH/sec, however, this approach became increasingly difficult because the nonce values were exhausted in less than a second. As ASIC mining equipment started pushing and then exceeding the TH/sec hash rate, the mining software needed more space for nonce values in order to find valid blocks. The timestamp could be stretched a bit, but moving it too far into the future would cause the block to become invalid. A new source of "change" was needed in the block header. The solution was to use the coinbase transaction as a source of extra nonce values. Because the coinbase script can store between 2 and 100 bytes of data, miners started using that space as extra nonce space, allowing them to explore a much larger range of block header values to find valid blocks. The coinbase transaction is included in the merkle tree, which means that any change in the coinbase script causes the merkle root to change. Eight bytes of extra nonce, plus the 4 bytes of "standard" nonce allow miners to explore a total 296 (8 followed by 28 zeros) possibilities per second without having to modify the timestamp. If, in the future, miners could run through all these possibilities, they could then modify the timestamp. There is also more space in the coinbase script for future expansion of the extra nonce space.
Mining Pools
In this highly competitive environment, individual miners working alone (also known as solo miners) don’t stand a chance. The likelihood of them finding a block to offset their electricity and hardware costs is so low that it represents a gamble, like playing the lottery. Even the fastest consumer ASIC mining system cannot keep up with commercial systems that stack tens of thousands of these chips in giant warehouses near hydroelectric powerstations. Miners now collaborate to form mining pools, pooling their hashing power and sharing the reward among thousands of participants. By participating in a pool, miners get a smaller share of the overall reward, but typically get rewarded every day, reducing uncertainty.
Let’s look at a specific example. Assume a miner has purchased mining hardware with a combined hashing rate of 14,000 gigahashes per second (GH/s), or 14 TH/s. In 2017 this equipment costs approximately $2,500 USD. The hardware consumes 1375 watts (1.3 kW) of electricity when running, 32 kW-hours a day, at a cost of $1 to $2 per day at very low electricity rates. At current bitcoin difficulty, the miner will be able to solo mine a block approximately once every 4 years. If the miner does find a single block in that timeframe, the payout of 12.5 bitcoin, at approximately $1,000 per bitcoin, will result in a single payout of $12,500, which will not even cover the entire cost of the hardware and the electricity consumed over the time period, leaving a net loss of approximately $1,000. However, the chance of finding a block in a 4-year period depends on the miner’s luck. He might find two blocks in 4 years and make a very large profit. Or he might not find a block for 5 years and suffer a bigger financial loss. Even worse, the difficulty of the bitcoin Proof-of-Work algorithm is likely to go up significantly over that period, at the current rate of growth of hashing power, meaning the miner has, at most, one year to break even before the hardware is effectively obsolete and must be replaced by more powerful mining hardware. If this miner participates in a mining pool, instead of waiting for a once-in-four-years $12,500 windfall, he will be able to earn approximately $50 to $60 per week. The regular payouts from a mining pool will help him amortize the cost of hardware and electricity over time without taking an enormous risk. The hardware will still be obsolete in one or two years and the risk is still high, but the revenue is at least regular and reliable over that period. Financially this only makes sense at very low electricity cost (less than 1 cent per kW) and only at very large scale.
Mining pools coordinate many hundreds or thousands of miners, over specialized pool-mining protocols. The individual miners configure their mining equipment to connect to a pool server, after creating an account with the pool. Their mining hardware remains connected to the pool server while mining, synchronizing their efforts with the other miners. Thus, the pool miners share the effort to mine a block and then share in the rewards.
Successful blocks pay the reward to a pool bitcoin address, rather than individual miners. The pool server will periodically make payments to the miners' bitcoin addresses, once their share of the rewards has reached a certain threshold. Typically, the pool server charges a percentage fee of the rewards for providing the pool-mining service.
Miners participating in a pool split the work of searching for a solution to a candidate block, earning "shares" for their mining contribution. The mining pool sets a higher target (lower difficulty) for earning a share, typically more than 1,000 times easier than the bitcoin network’s target. When someone in the pool successfully mines a block, the reward is earned by the pool and then shared with all miners in proportion to the number of shares they contributed to the effort.
Pools are open to any miner, big or small, professional or amateur. A pool will therefore have some participants with a single small mining machine, and others with a garage full of high-end mining hardware. Some will be mining with a few tens of a kilowatt of electricity, others will be running a data center consuming a megawatt of power. How does a mining pool measure the individual contributions, so as to fairly distribute the rewards, without the possibility of cheating? The answer is to use bitcoin’s Proof-of-Work algorithm to measure each pool miner’s contribution, but set at a lower difficulty so that even the smallest pool miners win a share frequently enough to make it worthwhile to contribute to the pool. By setting a lower difficulty for earning shares, the pool measures the amount of work done by each miner. Each time a pool miner finds a block header hash that is less than the pool target, she proves she has done the hashing work to find that result. More importantly, the work to find shares contributes, in a statistically measurable way, to the overall effort to find a hash lower than the bitcoin network’s target. Thousands of miners trying to find low-value hashes will eventually find one low enough to satisfy the bitcoin network target.
Let’s return to the analogy of a dice game. If the dice players are throwing dice with a goal of throwing less than four (the overall network difficulty), a pool would set an easier target, counting how many times the pool players managed to throw less than eight. When pool players throw less than eight (the pool share target), they earn shares, but they don’t win the game because they don’t achieve the game target (less than four). The pool players will achieve the easier pool target much more often, earning them shares very regularly, even when they don’t achieve the harder target of winning the game. Every now and then, one of the pool players will throw a combined dice throw of less than four and the pool wins. Then, the earnings can be distributed to the pool players based on the shares they earned. Even though the target of eight-or-less wasn’t winning, it was a fair way to measure dice throws for the players, and it occasionally produces a less-than-four throw.
Similarly, a mining pool will set a (higher and easier) pool target that will ensure that an individual pool miner can find block header hashes that are less than the pool target often, earning shares. Every now and then, one of these attempts will produce a block header hash that is less than the bitcoin network target, making it a valid block and the whole pool wins.
Managed pools
Most mining pools are "managed," meaning that there is a company or individual running a pool server. The owner of the pool server is called the pool operator, and he charges pool miners a percentage fee of the earnings.
The pool server runs specialized software and a pool-mining protocol that coordinate the activities of the pool miners. The pool server is also connected to one or more full bitcoin nodes and has direct access to a full copy of the blockchain database. This allows the pool server to validate blocks and transactions on behalf of the pool miners, relieving them of the burden of running a full node. For pool miners, this is an important consideration, because a full node requires a dedicated computer with at least 100 to 150 GB of persistent storage (disk) and at least 2 to 4 GB of memory (RAM). Furthermore, the bitcoin software running on the full node needs to be monitored, maintained, and upgraded frequently. Any downtime caused by a lack of maintenance or lack of resources will hurt the miner’s profitability. For many miners, the ability to mine without running a full node is another big benefit of joining a managed pool.
Pool miners connect to the pool server using a mining protocol such as Stratum (STM) or GetBlockTemplate (GBT). An older standard called GetWork (GWK) has been mostly obsolete since late 2012, because it does not easily support mining at hash rates above 4 GH/s. Both the STM and GBT protocols create block templates that contain a template of a candidate block header. The pool server constructs a candidate block by aggregating transactions, adding a coinbase transaction (with extra nonce space), calculating the merkle root, and linking to the previous block hash. The header of the candidate block is then sent to each of the pool miners as a template. Each pool miner then mines using the block template, at a higher (easier) target than the bitcoin network target, and sends any successful results back to the pool server to earn shares.
Peer-to-peer mining pool (P2Pool)
Managed pools create the possibility of cheating by the pool operator, who might direct the pool effort to double-spend transactions or invalidate blocks (see [consensus_attacks]). Furthermore, centralized pool servers represent a single-point-of-failure. If the pool server is down or is slowed by a denial-of-service attack, the pool miners cannot mine. In 2011, to resolve these issues of centralization, a new pool mining method was proposed and implemented: P2Pool, a peer-to-peer mining pool without a central operator.
P2Pool works by decentralizing the functions of the pool server, implementing a parallel blockchain-like system called a share chain. A share chain is a blockchain running at a lower difficulty than the bitcoin blockchain. The share chain allows pool miners to collaborate in a decentralized pool by mining shares on the share chain at a rate of one share block every 30 seconds. Each of the blocks on the share chain records a proportionate share reward for the pool miners who contribute work, carrying the shares forward from the previous share block. When one of the share blocks also achieves the bitcoin network target, it is propagated and included on the bitcoin blockchain, rewarding all the pool miners who contributed to all the shares that preceded the winning share block. Essentially, instead of a pool server keeping track of pool miner shares and rewards, the share chain allows all pool miners to keep track of all shares using a decentralized consensus mechanism like bitcoin’s blockchain consensus mechanism.
P2Pool mining is more complex than pool mining because it requires that the pool miners run a dedicated computer with enough disk space, memory, and internet bandwidth to support a full bitcoin node and the P2Pool node software. P2Pool miners connect their mining hardware to their local P2Pool node, which simulates the functions of a pool server by sending block templates to the mining hardware. On P2Pool, individual pool miners construct their own candidate blocks, aggregating transactions much like solo miners, but then mine collaboratively on the share chain. P2Pool is a hybrid approach that has the advantage of much more granular payouts than solo mining, but without giving too much control to a pool operator like managed pools.
Even though P2Pool reduces the concentration of power by mining pool operators, it is conceivably vulnerable to 51% attacks against the share chain itself. A much broader adoption of P2Pool does not solve the 51% attack problem for bitcoin itself. Rather, P2Pool makes bitcoin more robust overall, as part of a diversified mining ecosystem.
Consensus Attacks
Bitcoin’s consensus mechanism is, at least theoretically, vulnerable to attack by miners (or pools) that attempt to use their hashing power to dishonest or destructive ends. As we saw, the consensus mechanism depends on having a majority of the miners acting honestly out of self-interest. However, if a miner or group of miners can achieve a significant share of the mining power, they can attack the consensus mechanism so as to disrupt the security and availability of the bitcoin network.
It is important to note that consensus attacks can only affect future consensus, or at best, the most recent past (tens of blocks). Bitcoin’s ledger becomes more and more immutable as time passes. While in theory, a fork can be achieved at any depth, in practice, the computing power needed to force a very deep fork is immense, making old blocks practically immutable. Consensus attacks also do not affect the security of the private keys and signing algorithm (ECDSA). A consensus attack cannot steal bitcoin, spend bitcoin without signatures, redirect bitcoin, or otherwise change past transactions or ownership records. Consensus attacks can only affect the most recent blocks and cause denial-of-service disruptions on the creation of future blocks.
One attack scenario against the consensus mechanism is called the "51% attack." In this scenario a group of miners, controlling a majority (51%) of the total network’s hashing power, collude to attack bitcoin. With the ability to mine the majority of the blocks, the attacking miners can cause deliberate "forks" in the blockchain and double-spend transactions or execute denial-of-service attacks against specific transactions or addresses. A fork/double-spend attack is where the attacker causes previously confirmed blocks to be invalidated by forking below them and re-converging on an alternate chain. With sufficient power, an attacker can invalidate six or more blocks in a row, causing transactions that were considered immutable (six confirmations) to be invalidated. Note that a double-spend can only be done on the attacker’s own transactions, for which the attacker can produce a valid signature. Double-spending one’s own transactions is profitable if by invalidating a transaction the attacker can get an irreversible exchange payment or product without paying for it.
Let’s examine a practical example of a 51% attack. In the first chapter, we looked at a transaction between Alice and Bob for a cup of coffee. Bob, the cafe owner, is willing to accept payment for cups of coffee without waiting for confirmation (mining in a block), because the risk of a double-spend on a cup of coffee is low in comparison to the convenience of rapid customer service. This is similar to the practice of coffee shops that accept credit card payments without a signature for amounts below $25, because the risk of a credit-card chargeback is low while the cost of delaying the transaction to obtain a signature is comparatively larger. In contrast, selling a more expensive item for bitcoin runs the risk of a double-spend attack, where the buyer broadcasts a competing transaction that spends the same inputs (UTXO) and cancels the payment to the merchant. A double-spend attack can happen in two ways: either before a transaction is confirmed, or if the attacker takes advantage of a blockchain fork to undo several blocks. A 51% attack allows attackers to double-spend their own transactions in the new chain, thus undoing the corresponding transaction in the old chain.
In our example, malicious attacker Mallory goes to Carol’s gallery and purchases a beautiful triptych painting depicting Satoshi Nakamoto as Prometheus. Carol sells "The Great Fire" paintings for $250,000 in bitcoin to Mallory. Instead of waiting for six or more confirmations on the transaction, Carol wraps and hands the paintings to Mallory after only one confirmation. Mallory works with an accomplice, Paul, who operates a large mining pool, and the accomplice launches a 51% attack as soon as Mallory’s transaction is included in a block. Paul directs the mining pool to remine the same block height as the block containing Mallory’s transaction, replacing Mallory’s payment to Carol with a transaction that double-spends the same input as Mallory’s payment. The double-spend transaction consumes the same UTXO and pays it back to Mallory’s wallet, instead of paying it to Carol, essentially allowing Mallory to keep the bitcoin. Paul then directs the mining pool to mine an additional block, so as to make the chain containing the double-spend transaction longer than the original chain (causing a fork below the block containing Mallory’s transaction). When the blockchain fork resolves in favor of the new (longer) chain, the double-spent transaction replaces the original payment to Carol. Carol is now missing the three paintings and also has no bitcoin payment. Throughout all this activity, Paul’s mining pool participants might remain blissfully unaware of the double-spend attempt, because they mine with automated miners and cannot monitor every transaction or block.
To protect against this kind of attack, a merchant selling large-value items must wait at least six confirmations before giving the product to the buyer. Alternatively, the merchant should use an escrow multisignature account, again waiting for several confirmations after the escrow account is funded. The more confirmations elapse, the harder it becomes to invalidate a transaction with a 51% attack. For high-value items, payment by bitcoin will still be convenient and efficient even if the buyer has to wait 24 hours for delivery, which would correspond to approximately 144 confirmations.
In addition to a double-spend attack, the other scenario for a consensus attack is to deny service to specific bitcoin participants (specific bitcoin addresses). An attacker with a majority of the mining power can simply ignore specific transactions. If they are included in a block mined by another miner, the attacker can deliberately fork and remine that block, again excluding the specific transactions. This type of attack can result in a sustained denial-of-service against a specific address or set of addresses for as long as the attacker controls the majority of the mining power.
Despite its name, the 51% attack scenario doesn’t actually require 51% of the hashing power. In fact, such an attack can be attempted with a smaller percentage of the hashing power. The 51% threshold is simply the level at which such an attack is almost guaranteed to succeed. A consensus attack is essentially a tug-of-war for the next block and the "stronger" group is more likely to win. With less hashing power, the probability of success is reduced, because other miners control the generation of some blocks with their "honest" mining power. One way to look at it is that the more hashing power an attacker has, the longer the fork he can deliberately create, the more blocks in the recent past he can invalidate, or the more blocks in the future he can control. Security research groups have used statistical modeling to claim that various types of consensus attacks are possible with as little as 30% of the hashing power.
The massive increase of total hashing power has arguably made bitcoin impervious to attacks by a single miner. There is no possible way for a solo miner to control more than a small percentage of the total mining power. However, the centralization of control caused by mining pools has introduced the risk of for-profit attacks by a mining pool operator. The pool operator in a managed pool controls the construction of candidate blocks and also controls which transactions are included. This gives the pool operator the power to exclude transactions or introduce double-spend transactions. If such abuse of power is done in a limited and subtle way, a pool operator could conceivably profit from a consensus attack without being noticed.
Not all attackers will be motivated by profit, however. One potential attack scenario is where an attacker intends to disrupt the bitcoin network without the possibility of profiting from such disruption. A malicious attack aimed at crippling bitcoin would require enormous investment and covert planning, but could conceivably be launched by a well-funded, most likely state-sponsored, attacker. Alternatively, a well-funded attacker could attack bitcoin’s consensus by simultaneously amassing mining hardware, compromising pool operators, and attacking other pools with denial-of-service. All of these scenarios are theoretically possible, but increasingly impractical as the bitcoin network’s overall hashing power continues to grow exponentially.
Undoubtedly, a serious consensus attack would erode confidence in bitcoin in the short term, possibly causing a significant price decline. However, the bitcoin network and software are constantly evolving, so consensus attacks would be met with immediate countermeasures by the bitcoin community, making bitcoin hardier, stealthier, and more robust than ever.
Changing the Consensus Rules
The rules of consensus determine the validity of transactions and blocks. These rules are the basis for collaboration between all bitcoin nodes and are responsible for the convergence of all local perspectives into a single consistent blockchain across the entire network.
While the consensus rules are invariable in the short term and must be consistent across all nodes, they are not invariable in the long term. In order to evolve and develop the bitcoin system, the rules have to change from time to time to accommodate new features, improvements, or bug fixes. Unlike traditional software development, however, upgrades to a consensus system are much more difficult and require coordination between all the participants.
Hard Forks
In [forks] we looked at how the bitcoin network may briefly diverge, with two parts of the network following two different branches of the blockchain for a short time. We saw how this process occurs naturally, as part of the normal operation of the network and how the network reconverges on a common blockchain after one or more blocks are mined.
There is another scenario in which the network may diverge into following two chains: a change in the consensus rules. This type of fork is called a hard fork, because after the fork the network does not reconverge onto a single chain. Instead, the two chains evolve independently. Hard forks occur when part of the network is operating under a different set of consensus rules than the rest of the network. This may occur because of a bug or because of a deliberate change in the implementation of the consensus rules.
Hard forks can be used to change the rules of consensus, but they require coordination between all participants in the system. Any nodes that do not upgrade to the new consensus rules are unable to participate in the consensus mechanism and are forced onto a separate chain at the moment of the hard fork. Thus, a change introduced by a hard fork can be thought of as not "forward compatible," in that nonupgraded systems can no longer process the new consensus rules.
Let’s examine the mechanics of a hard fork with a specific example.
[blockchainwithforks] shows a blockchain with two forks. At block height 4, a one-block fork occurs. This is the type of spontaneous fork we saw in [forks]. With the mining of block 5, the network reconverges on one chain and the fork is resolved.
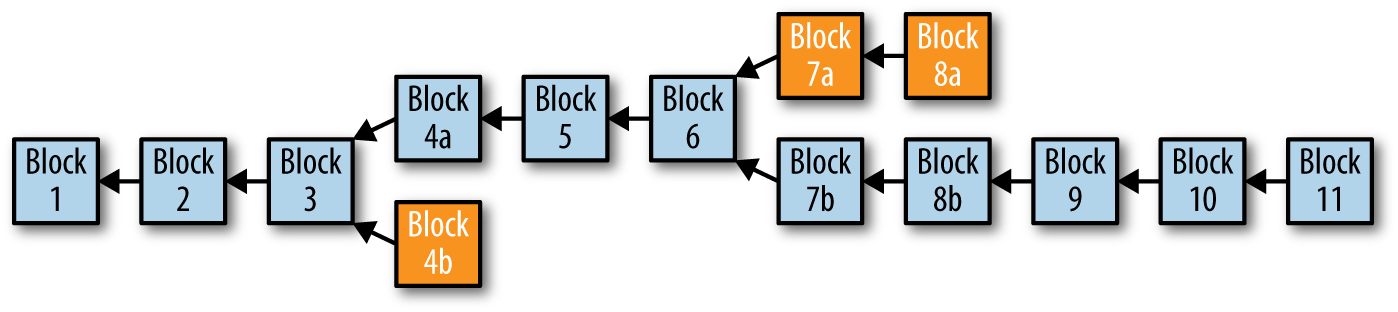
Later, however, at block height 6, a hard fork occurs. Let’s assume that a new implementation of the client is released with a change in the consensus rules. Starting on block height 7, miners running this new implementation will accept a new type of digital signature, let’s call it a "Smores" signature, that is not ECDSA based. Immediately after, a node running the new implementation creates a transaction that contains a Smores signature and a miner with the updated software mines block 7b containing this transaction.
Any node or miner that has not upgraded the software to validate Smores signatures is now unable to process block 7b. From their perspective, both the transaction that contained a Smores signature and block 7b that contained that transaction are invalid, because they are evaluating them based upon the old consensus rules. These nodes will reject the transaction and the block and will not propagate them. Any miners that are using the old rules will not accept block 7b and will continue to mine a candidate block whose parent is block 6. In fact, miners using the old rules may not even receive block 7b if all the nodes they are connected to are also obeying the old rules and therefore not propagating the block. Eventually, they will be able to mine block 7a, which is valid under the old rules and does not contain any transactions with Smores signatures.
The two chains continue to diverge from this point. Miners on the "b" chain will continue to accept and mine transactions containing Smores signatures, while miners on the "a" chain will continue to ignore these transactions. Even if block 8b does not contain any Smores-signed transactions, the miners on the "a" chain cannot process it. To them it appears to be an orphan block, as its parent "7b" is not recognized as a valid block.
Hard Forks: Software, Network, Mining, and Chain
For software developers, the term "fork" has another meaning, adding confusion to the term "hard fork." In open source software, a fork occurs when a group of developers choose to follow a different software roadmap and start a competing implementation of an open source project. We’ve already discussed two circumstances that will lead to a hard fork: a bug in the consensus rules and a deliberate modification of the consensus rules. In the case of a deliberate change to the consensus rules, a software fork precedes the hard fork. However, for this type of hard fork to occur, a new software implementation of the consensus rules must be developed, adopted, and launched.
Examples of software forks that have attempted to change consensus rules include Bitcoin XT, Bitcoin Classic, and most recently Bitcoin Unlimited. However, none of these software forks have resulted in a hard fork. While a software fork is a necessary precondition, it is not in itself sufficient for a hard fork to occur. For a hard fork to occur, the competing implementation must be adopted and the new rules activated, by miners, wallets, and intermediary nodes. Conversely, there are numerous alternative implementations of Bitcoin Core, and even software forks, that do not change the consensus rules and barring a bug, can coexist on the network and interoperate without causing a hard fork.
Consensus rules may differ in obvious and explicit ways, in the validation of transactions or blocks. The rules may also differ in more subtle ways, in the implementation of the consensus rules as they apply to bitcoin scripts or cryptographic primitives such as digital signatures. Finally, the consensus rules may differ in unanticipated ways because of implicit consensus constraints imposed by system limitations or implementation details. An example of the latter was seen in the unanticipated hard fork during the upgrade of Bitcoin Core 0.7 to 0.8, which was caused by a limitation in the Berkley DB implementation used to store blocks.
Conceptually, we can think of a hard fork as developing in four stages: a software fork, a network fork, a mining fork, and a chain fork.
The process begins when an alternative implementation of the client, with modified consensus rules, is created by developers.
When this forked implementation is deployed in the network, a certain percentage of miners, wallet users, and intermediate nodes may adopt and run this implementation. A resulting fork will depend upon whether the new consensus rules apply to blocks, transactions, or some other aspect of the system. If the new consensus rules pertain to transactions, then a wallet creating a transaction under the new rules may precipitate a network fork, followed by a hard fork when the transaction is mined into a block. If the new rules pertain to blocks, then the hard fork process will begin when a block is mined under the new rules.
First, the network will fork. Nodes based on the original implementation of the consensus rules will reject any transactions and blocks that are created under the new rules. Furthermore, the nodes following the original consensus rules will temporarily ban and disconnect from any nodes that are sending them these invalid transactions and blocks. As a result, the network will partition into two: old nodes will only remain connected to old nodes and new nodes will only be connected to new nodes. A single transaction or block based on the new rules will ripple through the network and result in the partition into two networks.
Once a miner using the new rules mines a block, the mining power and chain will also fork. New miners will mine on top of the new block, while old miners will mine a separate chain based on the old rules. The partitioned network will make it so that the miners operating on separate consensus rules won’t likely receive each other’s blocks, as they are connected to two separate networks.
Diverging Miners and Difficulty
As miners diverge into mining two different chains, the hashing power is split between the chains. The mining power can be split in any proportion between the two chains. The new rules may only be followed by a minority, or by the vast majority of the mining power.
Let’s assume, for example, an 80%–20% split, with the majority of the mining power using the new consensus rules. Let’s also assume that the fork occurs immediately after a retargeting period.
The two chains would each inherit the difficulty from the retargeting period. The new consensus rules would have 80% of the previously available mining power committed to them. From the perspective of this chain, the mining power has suddenly declined by 20% vis-a-vis the previous period. Blocks will be found on average every 12 minutes, representing the 20% decline in mining power available to extend this chain. This rate of block issuance will continue (barring any changes in hashing power) until 2016 blocks are mined, which will take approximately 24,192 minutes (at 12 minutes per block), or 16.8 days. After 16.8 days, a retarget will occur and the difficulty will adjust (reduced by 20%) to produce 10-minute blocks again, based on the reduced amount of hashing power in this chain.
The minority chain, mining under the old rules with only 20% of the hashing power, will face a much more difficult task. On this chain, blocks will now be mined every 50 minutes on average. The difficulty will not be adjusted for 2016 blocks, which will take 100,800 minutes, or approximately 10 weeks to mine. Assuming a fixed capacity per block, this will also result in a reduction of transaction capacity by a factor of 5, as there are fewer blocks per hour available to record transactions.
Contentious Hard Forks
This is the dawn of consensus software development. Just as open source development changed both the methods and products of software and created new methodologies, new tools, and new communities in its wake, consensus software development also represents a new frontier in computer science. Out of the debates, experiments, and tribulations of the bitcoin development roadmap, we will see new development tools, practices, methodologies, and communities emerge.
Hard forks are seen as risky because they force a minority to either upgrade or remain on a minority chain. The risk of splitting the entire system into two competing systems is seen by many as an unacceptable risk. As a result, many developers are reluctant to use the hard fork mechanism to implement upgrades to the consensus rules, unless there is near-unanimous support from the entire network. Any hard fork proposals that do not have near-unanimous support are considered too "contentious" to attempt without risking a partition of the system.
The issue of hard forks is highly controversial in the bitcoin development community, especially as it relates to any proposed changes to the consensus rules controlling the maximum block size limit. Some developers are opposed to any form of hard fork, seeing it as too risky. Others see the mechanism of hard fork as an essential tool for upgrading the consensus rules in a way that avoids "technical debt" and provides a clean break with the past. Finally, some developers see hard forks as a mechanism that should be used rarely, with a lot of advance planning and only under near-unanimous consensus.
Already we have seen the emergence of new methodologies to address the risks of hard forks. In the next section, we will look at soft forks, and the BIP-34 and BIP-9 methods for signaling and activation of consensus modifications.
Soft Forks
Not all consensus rule changes cause a hard fork. Only consensus changes that are forward-incompatible cause a fork. If the change is implemented in such a way that an unmodified client still sees the transaction or block as valid under the previous rules, the change can happen without a fork.
The term soft fork was introduced to distinguish this upgrade method from a "hard fork." In practice, a soft fork is not a fork at all. A soft fork is a forward-compatible change to the consensus rules that allows unupgraded clients to continue to operate in consensus with the new rules.
One aspect of soft forks that is not immediately obvious is that soft fork upgrades can only be used to constrain the consensus rules, not to expand them. In order to be forward compatible, transactions and blocks created under the new rules must be valid under the old rules too, but not vice versa. The new rules can only limit what is valid; otherwise, they will trigger a hard fork when rejected under the old rules.
Soft forks can be implemented in a number of ways—the term does not define a single method, rather a set of methods that all have one thing in common: they don’t require all nodes to upgrade or force nonupgraded nodes out of consensus.
Soft forks redefining NOP opcodes
A number of soft forks have been implemented in bitcoin, based on the re-interpretation of NOP opcodes. Bitcoin Script had ten opcodes reserved for future use, NOP1 through NOP10. Under the consensus rules, the presence of these opcodes in a script is interpreted as a null-potent operator, meaning they have no effect. Execution continues after the NOP opcode as if it wasn’t there.
A soft fork therefore can modify the semantics of a NOP code to give it new meaning. For example, BIP-65 (CHECKLOCKTIMEVERIFY) reinterpreted the NOP2 opcode. Clients implementing BIP-65 interpret NOP2 as OP_CHECKLOCKTIMEVERIFY and impose an absolute locktime consensus rule on UTXO that contain this opcode in their locking scripts. This change is a soft fork because a transaction that is valid under BIP-65 is also valid on any client that is not implementing (ignorant of) BIP-65. To the old clients, the script contains an NOP code, which is ignored.
Other ways to soft fork upgrade
The reinterpretation of NOP opcodes was both planned for and an obvious mechanism for consensus upgrades. Recently, however, another soft fork mechanism was introduced that does not rely on NOP opcodes for a very specific type of consensus change. This is examined in more detail in [segwit]. Segwit is an architectural change to the structure of a transaction, which moves the unlocking script (witness) from inside the transaction to an external data structure (segregating it). Segwit was initially envisioned as a hard fork upgrade, as it modified a fundamental structure (transaction). In November 2015, a developer working on Bitcoin Core proposed a mechanism by which segwit could be introduced as a soft fork. The mechanism used for this is a modification of the locking script of UTXO created under segwit rules, such that unmodified clients see the locking script as redeemable with any unlocking script whatsoever. As a result, segwit can be introduced without requiring every node to upgrade or split from the chain: a soft fork.
It is likely that there are other, yet to be discovered, mechanisms by which upgrades can be made in a forward-compatible way as a soft fork.
Criticisms of Soft Forks
Soft forks based on the NOP opcodes are relatively uncontroversial. The NOP opcodes were placed in Bitcoin Script with the explicit goal of allowing non-disruptive upgrades.
However, many developers are concerned that other methods of soft fork upgrades make unacceptable tradeoffs. Common criticisms of soft fork changes include:
- Technical debt
-
Because soft forks are more technically complex than a hard fork upgrade, they introduce technical debt, a term that refers to increasing the future cost of code maintenance because of design tradeoffs made in the past. Code complexity in turn increases the likelihood of bugs and security vulnerabilities.
- Validation relaxation
-
Unmodified clients see transactions as valid, without evaluating the modified consensus rules. In effect, the unmodified clients are not validating using the full range of consensus rules, as they are blind to the new rules. This applies to NOP-based upgrades, as well as other soft fork upgrades.
- Irreversible upgrades
-
Because soft forks create transactions with additional consensus constraints, they become irreversible upgrades in practice. If a soft fork upgrade were to be reversed after being activated, any transactions created under the new rules could result in a loss of funds under the old rules. For example, if a CLTV transaction is evaluated under the old rules, there is no timelock constraint and it can be spent whenever. Therefore, critics contend that a failed soft fork that had to be reversed because of a bug would almost certainly lead to loss of funds.
Soft Fork Signaling with Block Version
Since soft forks allow unmodified clients to continue to operate within consensus, the mechanism for "activating" a soft fork is through miners signaling readiness: a majority of miners must agree that they are ready and willing to enforce the new consensus rules. To coordinate their actions, there is a signaling mechanism that allows them to show their support for a consensus rule change. This mechanism was introduced with the activation of BIP-34 in March 2013 and replaced by the activation of BIP-9 in July 2016.
BIP-34 Signaling and Activation
The first implementation, in BIP-34, used the block version field to allow miners to signal readiness for a specific consensus rule change. Prior to BIP-34, the block version was set to "1" by convention not enforced by consensus.
BIP-34 defined a consensus rule change that required the coinbase field (input) of the coinbase transaction to contain the block height. Prior to BIP-34, the coinbase could contain any arbitrary data the miners chose to include. After activation of BIP-34, valid blocks had to contain a specific block-height at the beginning of the coinbase and be identified with a version number greater than or equal to "2."
To signal the change and activation of BIP-34, miners set the block version to "2," instead of "1." This did not immediately make version "1" blocks invalid. Once activated, version "1" blocks would become invalid and all version "2" blocks would be required to contain the block height in the coinbase to be valid.
BIP-34 defined a two-step activation mechanism, based on a rolling window of 1000 blocks. A miner would signal his or her individual readiness for BIP-34 by constructing blocks with "2" as the version number. Strictly speaking, these blocks did not yet have to comply with the new consensus rule of including the block-height in the coinbase transaction because the consensus rule had not yet been activated. The consensus rules activated in two steps:
-
If 75% (750 of the most recent 1000 blocks) are marked with version "2," then version "2" blocks must contain block height in the coinbase transaction or they are rejected as invalid. Version "1" blocks are still accepted by the network and do not need to contain block-height. The old and new consensus rules coexist during this period.
-
When 95% (950 of the most recent 1000 blocks) are version "2," version "1" blocks are no longer considered valid. Version "2" blocks are valid only if they contain the block-height in the coinbase (as per the previous threshold). Thereafter, all blocks must comply with the new consensus rules, and all valid blocks must contain block-height in the coinbase transaction.
After successful signaling and activation under the BIP-34 rules, this mechanism was used twice more to activate soft forks:
After the activation of BIP-65, the signaling and activation mechanism of BIP-34 was retired and replaced with the BIP-9 signaling mechanism described next.
The standard is defined in BIP-34 (Block v2, Height in Coinbase).
BIP-9 Signaling and Activation
The mechanism used by BIP-34, BIP-66, and BIP-65 was successful in activating three soft forks. However, it was replaced because it had several limitations:
-
By using the integer value of the block version, only one soft fork could be activated at a time, so it required coordination between soft fork proposals and agreement on their prioritization and sequencing.
-
Furthermore, because the block version was incremented, the mechanism didn’t offer a straightforward way to reject a change and then propose a different one. If old clients were still running, they could mistake signaling for a new change as signaling for the previously rejected change.
-
Each new change irrevocably reduced the available block versions for future changes.
BIP-9 was proposed to overcome these challenges and improve the rate and ease of implementing future changes.
BIP-9 interprets the block version as a bit field instead of an integer. Because the block version was originally used as an integer, versions 1 through 4, only 29 bits remain available to be used as a bit field. This leaves 29 bits that can be used to independently and simultaneously signal readiness on 29 different proposals.
BIP-9 also sets a maximum time for signaling and activation. This way miners don’t need to signal forever. If a proposal is not activated within the TIMEOUT period (defined in the proposal), the proposal is considered rejected. The proposal may be resubmitted for signaling with a different bit, renewing the activation period.
Furthermore, after the TIMEOUT has passed and a feature has been activated or rejected, the signaling bit can be reused for another feature without confusion. Therefore, up to 29 changes can be signaled in parallel and after TIMEOUT the bits can be "recycled" to propose new changes.
|
Note
|
While signaling bits can be reused or recycled, as long as the voting period does not overlap, the authors of BIP-9 recommend that bits are reused only when necessary; unexpected behavior could occur due to bugs in older software. In short, we should not expect to see reuse until all 29 bits have been used once. |
Proposed changes are identified by a data structure that contains the following fields:
- name
-
A short description used to distinguish between proposals. Most often the BIP describing the proposal, as "bipN," where N is the BIP number.
- bit
-
0 through 28, the bit in the block version that miners use to signal approval for this proposal.
- starttime
-
The time (based on Median Time Past, or MTP) that signaling starts after which the bit’s value is interpreted as signaling readiness for the proposal.
- endtime
-
The time (based on MTP) after which the change is considered rejected if it has not reached the activation threshold.
Unlike BIP-34, BIP-9 counts activation signaling in whole intervals based on the difficulty retarget period of 2016 blocks. For every retarget period, if the sum of blocks signaling for a proposal exceeds 95% (1916 of 2016), the proposal will be activated one retarget period later.
BIP-9 offers a proposal state diagram to illustrate the various stages and transitions for a proposal, as shown in [bip9states].
Proposals start in the DEFINED state, once their parameters are known (defined) in the bitcoin software. For blocks with MTP after the start time, the proposal state transitions to STARTED. If the voting threshold is exceeded within a retarget period and the timeout has not been exceeded, the proposal state transitions to LOCKED_IN. One retarget period later, the proposal becomes ACTIVE. Proposals remain in the ACTIVE state perpetually once they reach that state. If the timeout is elapsed before the voting threshold has been reached, the proposal state changes to FAILED, indicating a rejected proposal. REJECTED proposals remain in that state perpetually.
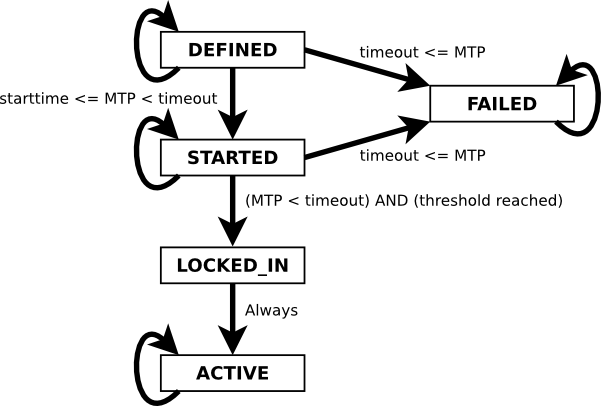
BIP-9 was first implemented for the activation of CHECKSEQUENCEVERIFY and associated BIPs (68, 112, 113). The proposal named "csv" was activated successfully in July of 2016.
The standard is defined in BIP-9 (Version bits with timeout and delay).
Consensus Software Development
Consensus software development continues to evolve and there is much discussion on the various mechanisms for changing the consensus rules. By its very nature, bitcoin sets a very high bar on coordination and consensus for changes. As a decentralized system, it has no "authority" that can impose its will on the participants of the network. Power is diffused between multiple constituencies such as miners, core developers, wallet developers, exchanges, merchants, and end users. Decisions cannot be made unilaterally by any of these constituencies. For example, while miners can theoretically change the rules by simple majority (51%), they are constrained by the consent of the other constituencies. If they act unilaterally, the rest of the participants may simply refuse to follow them, keeping the economic activity on a minority chain. Without economic activity (transactions, merchants, wallets, exchanges), the miners will be mining a worthless coin with empty blocks. This diffusion of power means that all the participants must coordinate, or no changes can be made. Status quo is the stable state of this system with only a few changes possible if there is strong consensus by a very large majority. The 95% threshold for soft forks is reflective of this reality.
It is important to recognize that there is no perfect solution for consensus development. Both hard forks and soft forks involve tradeoffs. For some types of changes, soft forks may be a better choice; for others, hard forks may be a better choice. There is no perfect choice; both carry risks. The one constant characteristic of consensus software development is that change is difficult and consensus forces compromise.
Some see this as a weakness of consensus systems. In time, you may come to see it as I do, as the system’s greatest strength.
Bitcoin Security
Securing bitcoin is challenging because bitcoin is not an abstract reference to value, like a balance in a bank account. Bitcoin is very much like digital cash or gold. You’ve probably heard the expression, "Possession is nine-tenths of the law." Well, in bitcoin, possession is ten-tenths of the law. Possession of the keys to unlock the bitcoin is equivalent to possession of cash or a chunk of precious metal. You can lose it, misplace it, have it stolen, or accidentally give the wrong amount to someone. In every one of these cases, users have no recourse, just as if they dropped cash on a public sidewalk.
However, bitcoin has capabilities that cash, gold, and bank accounts do not. A bitcoin wallet, containing your keys, can be backed up like any file. It can be stored in multiple copies, even printed on paper for hard-copy backup. You can’t "back up" cash, gold, or bank accounts. Bitcoin is different enough from anything that has come before that we need to think about bitcoin security in a novel way too.
Security Principles
The core principle in bitcoin is decentralization and it has important implications for security. A centralized model, such as a traditional bank or payment network, depends on access control and vetting to keep bad actors out of the system. By comparison, a decentralized system like bitcoin pushes the responsibility and control to the users. Because security of the network is based on Proof-of-Work, not access control, the network can be open and no encryption is required for bitcoin traffic.
On a traditional payment network, such as a credit card system, the payment is open-ended because it contains the user’s private identifier (the credit card number). After the initial charge, anyone with access to the identifier can "pull" funds and charge the owner again and again. Thus, the payment network has to be secured end-to-end with encryption and must ensure that no eavesdroppers or intermediaries can compromise the payment traffic, in transit or when it is stored (at rest). If a bad actor gains access to the system, he can compromise current transactions and payment tokens that can be used to create new transactions. Worse, when customer data is compromised, the customers are exposed to identity theft and must take action to prevent fraudulent use of the compromised accounts.
Bitcoin is dramatically different. A bitcoin transaction authorizes only a specific value to a specific recipient and cannot be forged or modified. It does not reveal any private information, such as the identities of the parties, and cannot be used to authorize additional payments. Therefore, a bitcoin payment network does not need to be encrypted or protected from eavesdropping. In fact, you can broadcast bitcoin transactions over an open public channel, such as unsecured WiFi or Bluetooth, with no loss of security.
Bitcoin’s decentralized security model puts a lot of power in the hands of the users. With that power comes responsibility for maintaining the secrecy of the keys. For most users that is not easy to do, especially on general-purpose computing devices such as internet-connected smartphones or laptops. Although bitcoin’s decentralized model prevents the type of mass compromise seen with credit cards, many users are not able to adequately secure their keys and get hacked, one by one.
Developing Bitcoin Systems Securely
The most important principle for bitcoin developers is decentralization. Most developers will be familiar with centralized security models and might be tempted to apply these models to their bitcoin applications, with disastrous results.
Bitcoin’s security relies on decentralized control over keys and on independent transaction validation by miners. If you want to leverage bitcoin’s security, you need to ensure that you remain within the bitcoin security model. In simple terms: don’t take control of keys away from users and don’t take transactions off the blockchain.
For example, many early bitcoin exchanges concentrated all user funds in a single "hot" wallet with keys stored on a single server. Such a design removes control from users and centralizes control over keys in a single system. Many such systems have been hacked, with disastrous consequences for their customers.
Another common mistake is to take transactions "off blockchain" in a misguided effort to reduce transaction fees or accelerate transaction processing. An "off blockchain" system will record transactions on an internal, centralized ledger and only occasionally synchronize them to the bitcoin blockchain. This practice, again, substitutes decentralized bitcoin security with a proprietary and centralized approach. When transactions are off blockchain, improperly secured centralized ledgers can be falsified, diverting funds and depleting reserves, unnoticed.
Unless you are prepared to invest heavily in operational security, multiple layers of access control, and audits (as the traditional banks do) you should think very carefully before taking funds outside of bitcoin’s decentralized security context. Even if you have the funds and discipline to implement a robust security model, such a design merely replicates the fragile model of traditional financial networks, plagued by identity theft, corruption, and embezzlement. To take advantage of bitcoin’s unique decentralized security model, you have to avoid the temptation of centralized architectures that might feel familiar but ultimately subvert bitcoin’s security.
The Root of Trust
Traditional security architecture is based upon a concept called the root of trust, which is a trusted core used as the foundation for the security of the overall system or application. Security architecture is developed around the root of trust as a series of concentric circles, like layers in an onion, extending trust outward from the center. Each layer builds upon the more-trusted inner layer using access controls, digital signatures, encryption, and other security primitives. As software systems become more complex, they are more likely to contain bugs, which make them vulnerable to security compromise. As a result, the more complex a software system becomes, the harder it is to secure. The root of trust concept ensures that most of the trust is placed within the least complex part of the system, and therefore least vulnerable, parts of the system, while more complex software is layered around it. This security architecture is repeated at different scales, first establishing a root of trust within the hardware of a single system, then extending that root of trust through the operating system to higher-level system services, and finally across many servers layered in concentric circles of diminishing trust.
Bitcoin security architecture is different. In bitcoin, the consensus system creates a trusted public ledger that is completely decentralized. A correctly validated blockchain uses the genesis block as the root of trust, building a chain of trust up to the current block. Bitcoin systems can and should use the blockchain as their root of trust. When designing a complex bitcoin application that consists of services on many different systems, you should carefully examine the security architecture in order to ascertain where trust is being placed. Ultimately, the only thing that should be explicitly trusted is a fully validated blockchain. If your application explicitly or implicitly vests trust in anything but the blockchain, that should be a source of concern because it introduces vulnerability. A good method to evaluate the security architecture of your application is to consider each individual component and evaluate a hypothetical scenario where that component is completely compromised and under the control of a malicious actor. Take each component of your application, in turn, and assess the impacts on the overall security if that component is compromised. If your application is no longer secure when components are compromised, that shows you have misplaced trust in those components. A bitcoin application without vulnerabilities should be vulnerable only to a compromise of the bitcoin consensus mechanism, meaning that its root of trust is based on the strongest part of the bitcoin security architecture.
The numerous examples of hacked bitcoin exchanges serve to underscore this point because their security architecture and design fails even under the most casual scrutiny. These centralized implementations had invested trust explicitly in numerous components outside the bitcoin blockchain, such as hot wallets, centralized ledger databases, vulnerable encryption keys, and similar schemes.
User Security Best Practices
Humans have used physical security controls for thousands of years. By comparison, our experience with digital security is less than 50 years old. Modern general-purpose operating systems are not very secure and not particularly suited to storing digital money. Our computers are constantly exposed to external threats via always-on internet connections. They run thousands of software components from hundreds of authors, often with unconstrained access to the user’s files. A single piece of rogue software, among the many thousands installed on your computer, can compromise your keyboard and files, stealing any bitcoin stored in wallet applications. The level of computer maintenance required to keep a computer virus-free and trojan-free is beyond the skill level of all but a tiny minority of computer users.
Despite decades of research and advancements in information security, digital assets are still woefully vulnerable to a determined adversary. Even the most highly protected and restricted systems, in financial services companies, intelligence agencies, and defense contractors, are frequently breached. Bitcoin creates digital assets that have intrinsic value and can be stolen and diverted to new owners instantly and irrevocably. This creates a massive incentive for hackers. Until now, hackers had to convert identity information or account tokens—such as credit cards and bank accounts—into value after compromising them. Despite the difficulty of fencing and laundering financial information, we have seen ever-escalating thefts. Bitcoin escalates this problem because it doesn’t need to be fenced or laundered; it is intrinsic value within a digital asset.
Fortunately, bitcoin also creates the incentives to improve computer security. Whereas previously the risk of computer compromise was vague and indirect, bitcoin makes these risks clear and obvious. Holding bitcoin on a computer serves to focus the user’s mind on the need for improved computer security. As a direct result of the proliferation and increased adoption of bitcoin and other digital currencies, we have seen an escalation in both hacking techniques and security solutions. In simple terms, hackers now have a very juicy target and users have a clear incentive to defend themselves.
Over the past three years, as a direct result of bitcoin adoption, we have seen tremendous innovation in the realm of information security in the form of hardware encryption, key storage and hardware wallets, multisignature technology, and digital escrow. In the following sections we will examine various best practices for practical user security.
Physical Bitcoin Storage
Because most users are far more comfortable with physical security than information security, a very effective method for protecting bitcoin is to convert them into physical form. Bitcoin keys are nothing more than long numbers. This means that they can be stored in a physical form, such as printed on paper or etched on a metal coin. Securing the keys then becomes as simple as physically securing the printed copy of the bitcoin keys. A set of bitcoin keys that is printed on paper is called a "paper wallet," and there are many free tools that can be used to create them. I personally keep the vast majority of my bitcoin (99% or more) stored on paper wallets, encrypted with BIP-38, with multiple copies locked in safes. Keeping bitcoin offline is called cold storage and it is one of the most effective security techniques. A cold storage system is one where the keys are generated on an offline system (one never connected to the internet) and stored offline either on paper or on digital media, such as a USB memory stick.
Hardware Wallets
In the long term, bitcoin security increasingly will take the form of hardware tamper-proof wallets. Unlike a smartphone or desktop computer, a bitcoin hardware wallet has just one purpose: to hold bitcoin securely. Without general-purpose software to compromise and with limited interfaces, hardware wallets can deliver an almost foolproof level of security to nonexpert users. I expect to see hardware wallets become the predominant method of bitcoin storage. For an example of such a hardware wallet, see the Trezor.
Balancing Risk
Although most users are rightly concerned about bitcoin theft, there is an even bigger risk. Data files get lost all the time. If they contain bitcoin, the loss is much more painful. In the effort to secure their bitcoin wallets, users must be very careful not to go too far and end up losing the bitcoin. In July 2011, a well-known bitcoin awareness and education project lost almost 7,000 bitcoin. In their effort to prevent theft, the owners had implemented a complex series of encrypted backups. In the end they accidentally lost the encryption keys, making the backups worthless and losing a fortune. Like hiding money by burying it in the desert, if you secure your bitcoin too well you might not be able to find it again.
Diversifying Risk
Would you carry your entire net worth in cash in your wallet? Most people would consider that reckless, yet bitcoin users often keep all their bitcoin in a single wallet. Instead, users should spread the risk among multiple and diverse bitcoin wallets. Prudent users will keep only a small fraction, perhaps less than 5%, of their bitcoin in an online or mobile wallet as "pocket change." The rest should be split between a few different storage mechanisms, such as a desktop wallet and offline (cold storage).
Multisig and Governance
Whenever a company or individual stores large amounts of bitcoin, they should consider using a multisignature bitcoin address. Multisignature addresses secure funds by requiring more than one signature to make a payment. The signing keys should be stored in a number of different locations and under the control of different people. In a corporate environment, for example, the keys should be generated independently and held by several company executives, to ensure no single person can compromise the funds. Multisignature addresses can also offer redundancy, where a single person holds several keys that are stored in different locations.
Survivability
One important security consideration that is often overlooked is availability, especially in the context of incapacity or death of the key holder. Bitcoin users are told to use complex passwords and keep their keys secure and private, not sharing them with anyone. Unfortunately, that practice makes it almost impossible for the user’s family to recover any funds if the user is not available to unlock them. In most cases, in fact, the families of bitcoin users might be completely unaware of the existence of the bitcoin funds.
If you have a lot of bitcoin, you should consider sharing access details with a trusted relative or lawyer. A more complex survivability scheme can be set up with multi-signature access and estate planning through a lawyer specialized as a "digital asset executor."
Conclusion
Bitcoin is a completely new, unprecedented, and complex technology. Over time we will develop better security tools and practices that are easier to use by nonexperts. For now, bitcoin users can use many of the tips discussed here to enjoy a secure and trouble-free bitcoin experience.
Blockchain Applications
Let’s now build on our understanding of bitcoin by looking at it as an application platform. Nowadays, many people use the term "blockchain" to refer to any application platform that shares the design principles of bitcoin. The term is often misused and applied to many things that fail to deliver the primary features that bitcoin’s blockchain delivers.
In this chapter we will look at the features offered by the bitcoin blockchain, as an application platform. We will consider the application building primitives, which form the building blocks of any blockchain application. We will look at several important applications that use these primitives, such as colored coins, payment (state) channels, and routed payment channels (Lightning Network).
Introduction
The bitcoin system was designed as a decentralized currency and payment system. However, most of its functionality is derived from much lower-level constructs that can be used for much broader applications. Bitcoin wasn’t built with components such as accounts, users, balances, and payments. Instead, it uses a transactional scripting language with low-level cryptographic functions, as we saw in [transactions]. Just like the higher-level concepts of accounts, balances, and payments can be derived from these basic primitives, so can many other complex applications. Thus, the bitcoin blockchain can become an application platform offering trust services to applications, such as smart contracts, far surpassing the original purpose of digital currency and payments.
Building Blocks (Primitives)
When operating correctly and over the long term, the bitcoin system offers certain guarantees, which can be used as building blocks to create applications. These include:
- No Double-Spend
-
The most fundamental guarantee of bitcoin’s decentralized consensus algorithm ensures that no UTXO can be spent twice.
- Immutability
-
Once a transaction is recorded in the blockchain and sufficient work has been added with subsequent blocks, the transaction’s data becomes immutable. Immutability is underwritten by energy, as rewriting the blockchain requires the expenditure of energy to produce Proof-of-Work. The energy required and therefore the degree of immutability increases with the amount of work committed on top of the block containing a transaction.
- Neutrality
-
The decentralized bitcoin network propagates valid transactions regardless of the origin or content of those transactions. This means that anyone can create a valid transaction with sufficient fees and trust they will be able to transmit that transaction and have it included in the blockchain at anytime.
- Secure Timestamping
-
The consensus rules reject any block whose timestamp is too far in the past or future. This ensures that timestamps on blocks can be trusted. The timestamp on a block implies an unspent-before guarantee for the inputs of all included transactions.
- Authorization
-
Digital signatures, validated in a decentralized network, offer authorization guarantees. Scripts that contain a requirement for a digital signature cannot be executed without authorization by the holder of the private key implied in the script.
- Auditability
-
All transactions are public and can be audited. All transactions and blocks can be linked back in an unbroken chain to the genesis block.
- Accounting
-
In any transaction (except the coinbase transaction) the value of inputs is equal to the value of outputs plus fees. It is not possible to create or destroy bitcoin value in a transaction. The outputs cannot exceed the inputs.
- Nonexpiration
-
A valid transaction does not expire. If it is valid today, it will be valid in the near future, as long as the inputs remain unspent and the consensus rules do not change.
- Integrity
-
A bitcoin transaction signed with
SIGHASH_ALLor parts of a transaction signed by anotherSIGHASHtype cannot be modified without invalidating the signature, thus invalidating the transaction itself. - Transaction Atomicity
-
Bitcoin transactions are atomic. They are either valid and confirmed (mined) or not. Partial transactions cannot be mined and there is no interim state for a transaction. At any point in time a transaction is either mined, or not.
- Discrete (Indivisible) Units of Value
-
Transaction outputs are discrete and indivisible units of value. They can either be spent or unspent, in full. They cannot be divided or partially spent.
- Quorum of Control
-
Multisignature constraints in scripts impose a quorum of authorization, predefined in the multisignature scheme. The M-of-N requirement is enforced by the consensus rules.
- Timelock/Aging
-
Any script clause containing a relative or absolute timelock can only be executed after its age exceeds the time specified.
- Replication
-
The decentralized storage of the blockchain ensures that when a transaction is mined, after sufficient confirmations, it is replicated across the network and becomes durable and resilient to power loss, data loss, etc.
- Forgery Protection
-
A transaction can only spend existing, validated outputs. It is not possible to create or counterfeit value.
- Consistency
-
In the absence of miner partitions, blocks that are recorded in the blockchain are subject to reorganization or disagreement with exponentially decreasing likelihood, based on the depth at which they are recorded. Once deeply recorded, the computation and energy required to change makes change practically infeasible.
- Recording External State
-
A transaction can commit a data value, via
OP_RETURN, representing a state transition in an external state machine. - Predictable Issuance
-
Less than 21 million bitcoin will be issued, at a predictable rate.
The list of building blocks is not complete and more are added with each new feature introduced into bitcoin.
Applications from Building Blocks
The building blocks offered by bitcoin are elements of a trust platform that can be used to compose applications. Here are some examples of applications that exist today and the building blocks they use:
- Proof-of-Existence (Digital Notary)
-
Immutability + Timestamp + Durability. A digital fingerprint can be committed with a transaction to the blockchain, proving that a document existed (Timestamp) at the time it was recorded. The fingerprint cannot be modified ex-post-facto (Immutability) and the proof will be stored permanently (Durability).
- Kickstarter (Lighthouse)
-
Consistency + Atomicity + Integrity. If you sign one input and the output (Integrity) of a fundraiser transaction, others can contribute to the fundraiser but it cannot be spent (Atomicity) until the goal (output value) is funded (Consistency).
- Payment Channels
-
Quorum of Control + Timelock + No Double Spend + Nonexpiration + Censorship Resistance + Authorization. A multisig 2-of-2 (Quorum) with a timelock (Timelock) used as the "settlement" transaction of a payment channel can be held (Nonexpiration) and spent whenever (Censorship Resistance) by either party (Authorization). The two parties can then create commitment transactions that double-spend (No Double-Spend) the settlement on a shorter timelock (Timelock).
Colored Coins
The first blockchain application we will discuss is colored coins.
Colored coins refers to a set of similar technologies that use bitcoin transactions to record the creation, ownership, and transfer of extrinsic assets other than bitcoin. By "extrinsic" we mean assets that are not stored directly on the bitcoin blockchain, as opposed to bitcoin itself, which is an asset intrinsic to the blockchain.
Colored coins are used to track digital assets as well as physical assets held by third parties and traded through colored coins certificates of ownership. Digital asset colored coins can represent intangible assets such as a stock certificate, license, virtual property (game items), or most any form of licensed intellectual property (trademarks, copyrights, etc.). Tangible asset colored coins can represent certificates of ownership of commodities (gold, silver, oil), land title, automobiles, boats, aircraft, etc.
The term derives from the idea of "coloring" or marking a nominal amount of bitcoin, for example, a single satoshi, to represent something other than the bitcoin value itself. As an analogy, consider stamping a $1 note with a message saying, "this is a stock certificate of ACME" or "this note can be redeemed for 1 oz of silver" and then trading the $1 note as a certificate of ownership of this other asset. The first implementation of colored coins, named Enhanced Padded-Order-Based Coloring or EPOBC, assigned extrinsic assets to a 1-satoshi output. In this way, it was a true "colored coin," as each asset was added as an attribute (color) of a single satoshi.
More recent implementations of colored coins use the OP_RETURN script opcode to store metadata in a transaction, in conjunction with external data stores that associate the metadata to specific assets.
The two most prominent implementations of colored coins today are Open Assets and Colored Coins by Colu. These two systems use different approaches to colored coins and are not compatible. Colored coins created in one system cannot be seen or used in the other system.
Using Colored Coins
Colored coins are created, transferred, and generally viewed in special wallets that can interpret the colored coins protocol metadata attached to bitcoin transactions. Special care must be taken to avoid using a colored-coin–related key in a regular bitcoin wallet, as the regular wallet may destroy the metadata. Similarly, colored coins should not be sent to addresses managed by regular wallets, but only to addresses that are managed by wallets that are colored-coin-aware. Both Colu and Open Assets systems use special colored-coin addresses to mitigate this risk and to ensure that colored coins are not sent to unaware wallets.
Colored coins are also not visible to most general-purpose blockchain explorers. Instead, you must use a colored-coins explorer to interpret the metadata of a colored coins transaction.
An Open Assets-compatible wallet application and blockchain explorer can be found at coinprism.
A Colu Colored Coins-compatible wallet application and blockchain explorer can be found at Blockchain Explorer.
A Copay wallet plug-in can be found at Colored Coins Copay Addon.
Issuing Colored Coins
Each of the colored coins implementations has a different way of creating colored coins, but they all provide similar functionality. The process of creating a colored coin asset is called issuance. An initial transaction, the issuance transaction registers the asset on the bitcoin blockchain and creates an asset ID that is used to reference the asset. Once issued, assets can be transferred between addresses using transfer transactions.
Assets issued as colored coins can have multiple properties. They can be divisible or indivisible, meaning that the amount of asset in a transfer can be an integer (e.g., 5) or have decimal subdivision (e.g., 4.321). Assets can also have fixed issuance, meaning a certain amount are issued only once, or can be reissued, meaning that new units of the asset can be issued by the original issuer after the initial issuance.
Finally, some colored coins enable dividends, allowing the distribution of bitcoin payments to the owners of a colored coin asset in proportion to their ownership.
Colored Coins Transactions
The metadata that gives meaning to a colored coin transaction is usually stored in one of the outputs using the OP_RETURN opcode. Different colored coins protocols use different encodings for the content of the OP_RETURN data. The output containing the OP_RETURN is called the marker output.
The order of the outputs and position of the marker output may have special meaning in the colored coins protocol. In Open Assets, for example, any outputs before the marker output represent asset issuance. Any outputs after the marker represent asset transfer. The marker output assigns specific values and colors to the other outputs by referencing their order in the transaction.
In Colored Coins (Colu), by comparison, the marker output encodes an opcode that determines how the metadata is interpreted. Opcodes 0x01 through 0x0F indicate an issuance transaction. An issuance opcode is usually followed by an asset ID or other identifier that can be used to retrieve the asset information from an external source (e.g., bittorrent). Opcodes 0x10 through 0x1F represent a transfer transaction. Transfer transaction metadata contain simple scripts that transfer specific amounts of assets from inputs to outputs, by reference to their index. Ordering of inputs and outputs is therefore important in the interpretation of the script.
If the metadata is too long to fit in OP_RETURN, the colored coins protocol may use other "tricks" to store metadata in a transaction. Examples include putting metadata in a redeem script, followed by OP_DROP opcodes to ensure the script ignores the metadata. Another mechanism used is a 1-of-N multisig script where only the first public key is a real public key that can spend the output and subsequent "keys" are replaced by encoded metadata.
In order to correctly interpret the metadata in a colored coins transaction you must use a compatible wallet or block explorer. Otherwise, the transaction looks like a "normal" bitcoin transaction with an OP_RETURN output.
As an example, I created and issued a MasterBTC asset using colored coins. The MasterBTC asset represents a voucher for a free copy of this book. These vouchers can be transferred, traded, and redeemed using a colored coins-compatible wallet.
For this particular example, I used the wallet and explorer at https://coinprism.info, which uses the Open Assets colored coins protocol.
[the_issuance_transaction_as_viewed_on_coinprismio] shows the issuance transaction using the Coinprism block explorer:
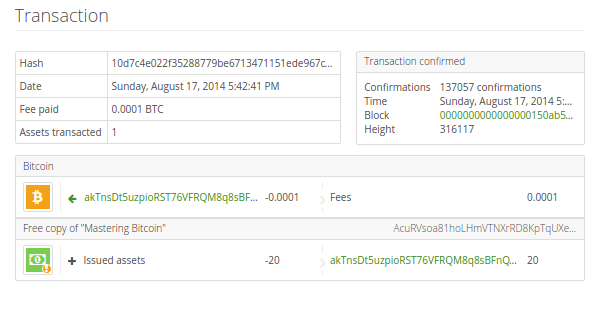
As you can see, coinprism shows the issuance of 20 units of "Free copy of Mastering Bitcoin," the MasterBTC asset, to a special colored coin address:
akTnsDt5uzpioRST76VFRQM8q8sBFnQiwcx|
Warning
|
Any funds or colored assets sent to this address will be lost forever. Do not send value to this example address! |
The transaction ID of the issuance transaction is a "normal" bitcoin transaction ID. [the_issuance_transaction_on_a_block] shows that same transaction in a block explorer that doesn’t decode colored coins. We’ll use blockchain.info:

As you can see, blockchain.info doesn’t recognize this as a colored coins transaction. In fact, it marks the second output with "Unable to decode output address" in red letters.
If you select "Show scripts & coinbase" on that screen, you can see more detail about the transaction ([the_scripts_in_the_issuance_transaction]).

Once again, blockchain.info doesn’t understand the second output. It marks it with "Strange" in red letters. However, we can see that some of the metadata in the marker output is human-readable:
OP_RETURN 4f41010001141b753d68747470733a2f2f6370722e736d2f466f796b777248365559
(decoded) "OA____u=https://cpr.sm/FoykwrH6UYLet’s retrieve the transaction using bitcoin-cli:
$ bitcoin-cli decoderawtransaction `bitcoin-cli getrawtransaction 10d7c4e022f35288779be6713471151ede967caaa39eecd35296aa36d9c109ec`Stripping out the rest of the transaction, the second output looks like this:
{ "value": 0.00000000, "n": 1, "scriptPubKey": "OP_RETURN 4f41010001141b753d68747470733a2f2f6370722e736d2f466f796b777248365559" }
The prefix 4F41 represents the letters "OA", which stands for "Open Assets" and helps us identify that what follows is metadata defined by the Open Assets protocol. The ASCII-encoded string that follows is a link to an asset definition:
u=https://cpr.sm/FoykwrH6UYIf we retrieve this URL, we get a JSON-encoded asset definition, as shown here:
{ "asset_ids": [ "AcuRVsoa81hoLHmVTNXrRD8KpTqUXeqwgH" ], "contract_url": null, "name_short": "MasterBTC", "name": "Free copy of \"Mastering Bitcoin\"", "issuer": "Andreas M. Antonopoulos", "description": "This token is redeemable for a free copy of the book \"Mastering Bitcoin\"", "description_mime": "text/x-markdown; charset=UTF-8", "type": "Other", "divisibility": 0, "link_to_website": false, "icon_url": null, "image_url": null, "version": "1.0" }
Counterparty
Counterparty is a protocol layer built on top of bitcoin. The Counterparty protocol, similar to colored coins, offers the ability to create and trade virtual assets and tokens. In addition, Counterparty offers a decentralized exchange for assets. Counterparty is also implementing smart contracts, based on the Ethereum Virtual Machine (EVM).
Like the colored coins protocols, Counterparty embeds metadata in bitcoin transactions, using the OP_RETURN opcode or 1-of-N multisignature addresses that encode metadata in the place of public keys. Using these mechanisms, Counterparty implements a protocol layer encoded in bitcoin transactions. The additional protocol layer can be interpreted by applications that are Counterparty-aware, such as wallets and blockchain explorers, or any application built using the Counterparty libraries.
Counterparty can be used as a platform for other applications and services, in turn. For example, Tokenly is a platform built on top of Counterparty that allows content creators, artists, and companies to issue tokens that express digital ownership and can be used to rent, access, trade, or shop for content, products, and services. Other applications leveraging Counterparty include games (Spells of Genesis) and grid computing projects (Folding Coin).
More details about Counterparty can be found at https://counterparty.io. The open source project can be found at https://github.com/CounterpartyXCP.
Payment Channels and State Channels
Payment channels are a trustless mechanism for exchanging bitcoin transactions between two parties, outside of the bitcoin blockchain. These transactions, which would be valid if settled on the bitcoin blockchain, are held off-chain instead, acting as promissory notes for eventual batch settlement. Because the transactions are not settled, they can be exchanged without the usual settlement latency, allowing extremely high transaction throughput, low (submillisecond) latency, and fine (satoshi-level) granularity.
Actually, the term channel is a metaphor. State channels are virtual constructs represented by the exchange of state between two parties, outside of the blockchain. There are no "channels" per se and the underlying data transport mechanism is not the channel. We use the term channel to represent the relationship and shared state between two parties, outside of the blockchain.
To further explain this concept, think of a TCP stream. From the perspective of higher-level protocols it is a "socket" connecting two applications across the internet. But if you look at the network traffic, a TCP stream is just a virtual channel over IP packets. Each endpoint of the TCP stream sequences and assembles IP packets to create the illusion of a stream of bytes. Underneath, it’s all disconnected packets. Similarly, a payment channel is just a series of transactions. If properly sequenced and connected, they create redeemable obligations that you can trust even though you don’t trust the other side of the channel.
In this section we will look at various forms of payment channels. First, we will examine the mechanisms used to construct a one-way (unidirectional) payment channel for a metered micropayment service, such as streaming video. Then, we will expand on this mechanism and introduce bidirectional payment channels. Finally, we will look at how bidirectional channels can be connected end-to-end to form multihop channels in a routed network, first proposed under the name Lightning Network.
Payment channels are part of the broader concept of a state channel, which represents an off-chain alteration of state, secured by eventual settlement in a blockchain. A payment channel is a state channel where the state being altered is the balance of a virtual currency.
State Channels—Basic Concepts and Terminology
A state channel is established between two parties, through a transaction that locks a shared state on the blockchain. This is called the funding transaction or anchor transaction. This single transaction must be transmitted to the network and mined to establish the channel. In the example of a payment channel, the locked state is the initial balance (in currency) of the channel.
The two parties then exchange signed transactions, called commitment transactions, that alter the initial state. These transactions are valid transactions in that they could be submitted for settlement by either party, but instead are held off-chain by each party pending the channel closure. State updates can be created as fast as each party can create, sign, and transmit a transaction to the other party. In practice this means that thousands of transactions per second can be exchanged.
When exchanging commitment transactions the two parties also invalidate the previous states, so that the most up-to-date commitment transaction is always the only one that can be redeemed. This prevents either party from cheating by unilaterally closing the channel with an expired prior state that is more favorable to them than the current state. We will examine the various mechanisms that can be used to invalidate prior state in the rest of this chapter.
Finally, the channel can be closed either cooperatively, by submitting a final settlement transaction to the blockchain, or unilaterally, by either party submitting the last commitment transaction to the blockchain. A unilateral close option is needed in case one of the parties unexpectedly disconnects. The settlement transaction represents the final state of the channel and is settled on the blockchain.
In the entire lifetime of the channel, only two transactions need to be submitted for mining on the blockchain: the funding and settlement transactions. In between these two states, the two parties can exchange any number of commitment transactions that are never seen by anyone else, nor submitted to the blockchain.
[payment_channel] illustrates a payment channel between Bob and Alice, showing the funding, commitment, and settlement transactions.
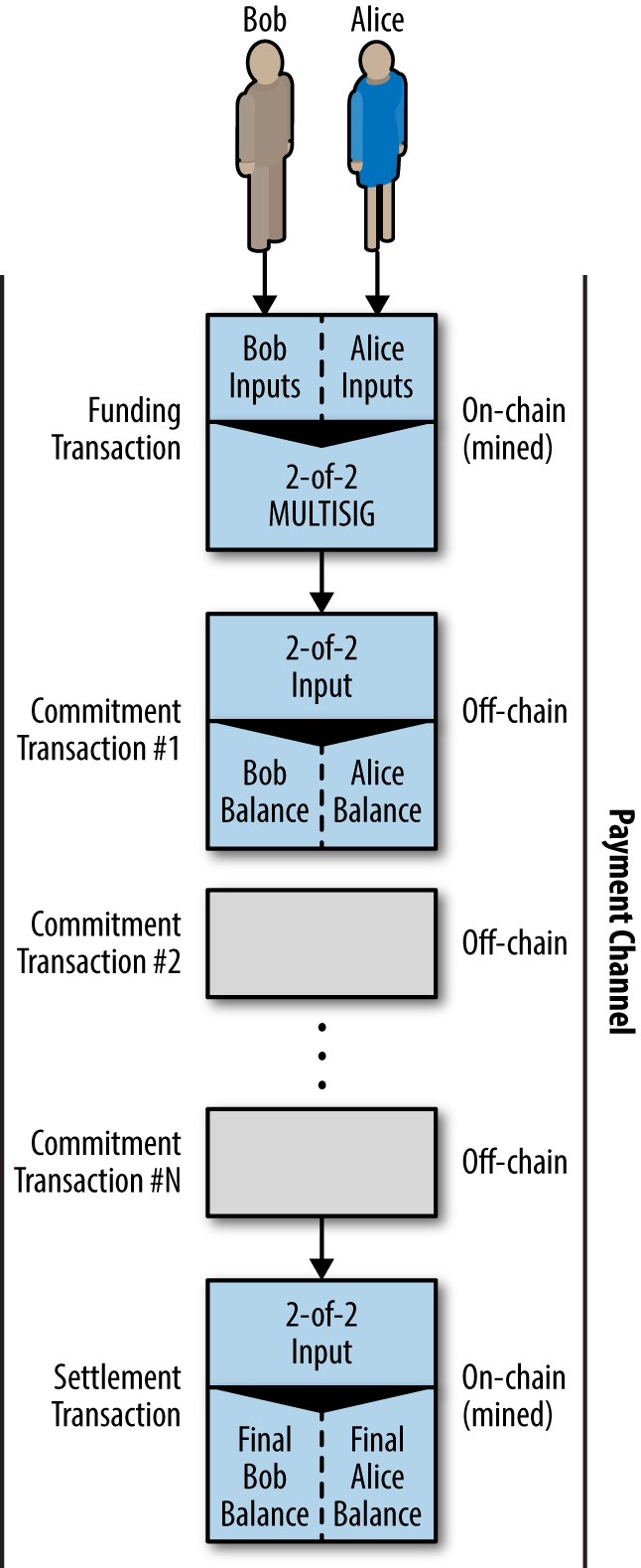
Simple Payment Channel Example
To explain state channels, we have to start with a very simple example. We demonstrate a one-way channel, meaning that value is flowing in one direction only. We will also start with the naive assumption that no one is trying to cheat, to keep things simple. Once we have the basic channel idea explained, we will then look at what it takes to make it trustless so that neither party can cheat, even if they are trying to.
For this example we will assume two participants: Emma and Fabian. Fabian offers a video streaming service that is billed by the second using a micropayment channel. Fabian charges 0.01 millibit (0.00001 BTC) per second of video, equivalent to 36 millibits (0.036 BTC) per hour of video. Emma is a user who purchases this streaming video service from Fabian. [emma_fabian_streaming_video] shows Emma buying the video streaming service from Fabian using a payment channel.
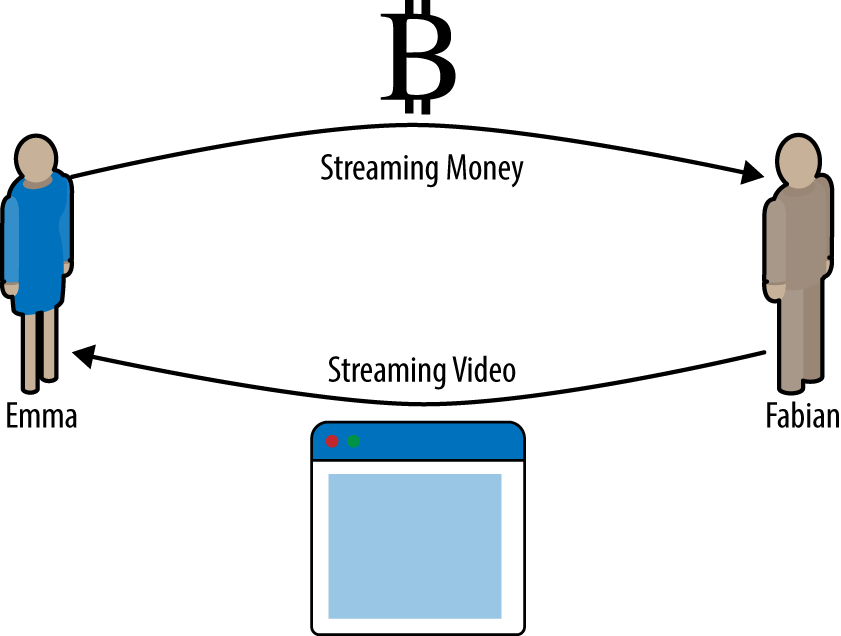
In this example, Fabian and Emma are using special software that handles both the payment channel and the video streaming. Emma is running the software in her browser, Fabian is running it on a server. The software includes basic bitcoin wallet functionality and can create and sign bitcoin transactions. Both the concept and the term "payment channel" are completely hidden from the users. What they see is video that is paid for by the second.
To set up the payment channel, Emma and Fabian establish a 2-of-2 multisignature address, with each of them holding one of the keys. From Emma’s perspective, the software in her browser presents a QR code with a P2SH address (starting with "3"), and asks her to submit a "deposit" for up to 1 hour of video. The address is then funded by Emma. Emma’s transaction, paying to the multisignature address, is the funding or anchor transaction for the payment channel.
For this example, let’s say that Emma funds the channel with 36 millibits (0.036 BTC). This will allow Emma to consume up to 1 hour of streaming video. The funding transaction in this case sets the maximum amount that can be transmitted in this channel, setting the channel capacity.
The funding transaction consumes one or more inputs from Emma’s wallet, sourcing the funds. It creates one output with a value of 36 millibits paid to the multisignature 2-of-2 address controlled jointly between Emma and Fabian. It may have additional outputs for change back to Emma’s wallet.
Once the funding transaction is confirmed, Emma can start streaming video. Emma’s software creates and signs a commitment transaction that changes the channel balance to credit 0.01 millibit to Fabian’s address and refund 35.99 millibits back to Emma. The transaction signed by Emma consumes the 36 millibits output created by the funding transaction and creates two outputs: one for her refund, the other for Fabian’s payment. The transaction is only partially signed—it requires two signatures (2-of-2), but only has Emma’s signature. When Fabian’s server receives this transaction, it adds the second signature (for the 2-of-2 input) and returns it to Emma together with 1 second worth of video. Now both parties have a fully signed commitment transaction that either can redeem, representing the correct up-to-date balance of the channel. Neither party broadcasts this transaction to the network.
In the next round, Emma’s software creates and signs another commitment transaction (commitment #2) that consumes the same 2-of-2 output from the funding transaction. The second commitment transaction allocates one output of 0.2 millibits to Fabian’s address and one output of 35.98 millibits back to Emma’s address. This new transaction is payment for two cumulative seconds of video. Fabian’s software signs and returns the second commitment transaction, together with the another second of video.
In this way, Emma’s software continues to send commitment transactions to Fabian’s server in exchange for streaming video. The balance of the channel gradually accumulates in favor of Fabian, as Emma consumes more seconds of video. Let’s say Emma watches 600 seconds (10 minutes) of video, creating and signing 600 commitment transactions. The last commitment transaction (#600) will have two outputs, splitting the balance of the channel, 6 millibits to Fabian and 30 millibits to Emma.
Finally, Emma clicks "Stop" to stop streaming video. Either Fabian or Emma can now transmit the final state transaction for settlement. This last transaction is the settlement transaction and pays Fabian for all the video Emma consumed, refunding the remainder of the funding transaction to Emma.
[video_payment_channel] shows the channel between Emma and Fabian and the commitment transactions that update the balance of the channel.
In the end, only two transactions are recorded on the blockchain: the funding transaction that established the channel and a settlement transaction that allocated the final balance correctly between the two participants.
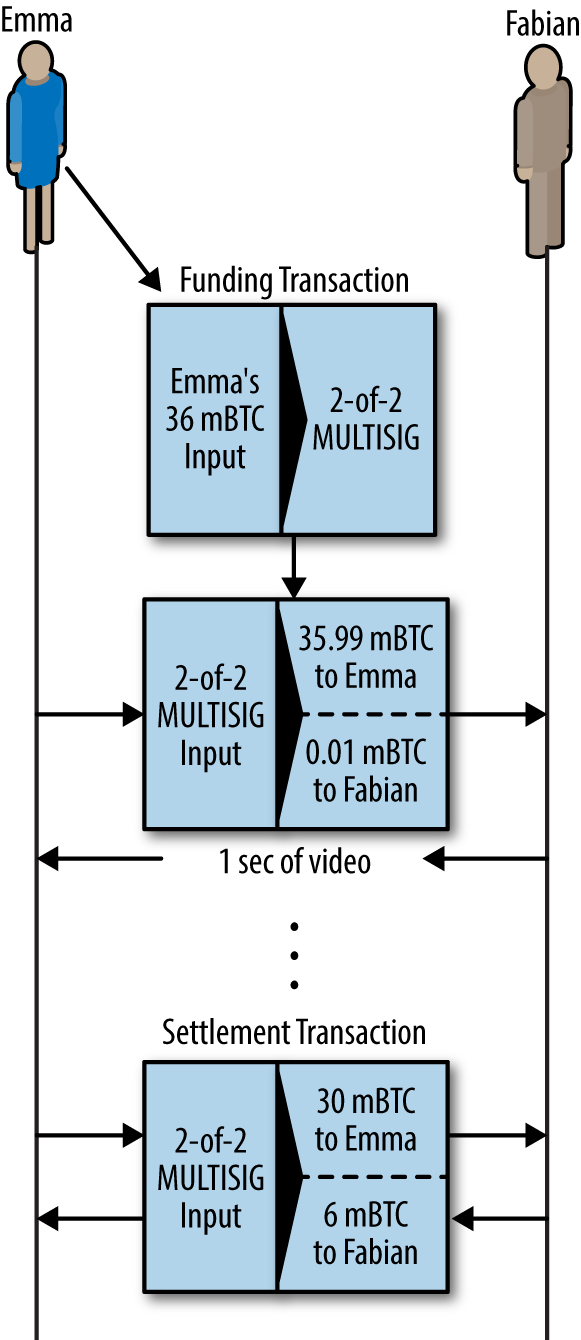
Making Trustless Channels
The channel we just described works, but only if both parties cooperate, without any failures or attempts to cheat. Let’s look at some of the scenarios that break this channel and see what is needed to fix those:
-
Once the funding transaction happens, Emma needs Fabian’s signature to get any money back. If Fabian disappears, Emma’s funds are locked in a 2-of-2 and effectively lost. This channel, as constructed, leads to a loss of funds if one of the parties disconnects before there is at least one commitment transaction signed by both parties.
-
While the channel is running, Emma can take any of the commitment transactions Fabian has countersigned and transmit one to the blockchain. Why pay for 600 seconds of video, if she can transmit commitment transaction #1 and only pay for 1 second of video? The channel fails because Emma can cheat by broadcasting a prior commitment that is in her favor.
Both of these problems can be solved with timelocks—let’s look at how we could use transaction-level timelocks (nLocktime).
Emma cannot risk funding a 2-of-2 multisig unless she has a guaranteed refund. To solve this problem, Emma constructs the funding and refund transaction at the same time. She signs the funding transaction but doesn’t transmit it to anyone. Emma transmits only the refund transaction to Fabian and obtains his signature.
The refund transaction acts as the first commitment transaction and its timelock establishes the upper bound for the channel’s life. In this case, Emma could set the nLocktime to 30 days or 4320 blocks into the future. All subsequent commitment transactions must have a shorter timelock, so that they can be redeemed before the refund transaction.
Now that Emma has a fully signed refund transaction, she can confidently transmit the signed funding transaction knowing that she can eventually, after the timelock expires, redeem the refund transaction even if Fabian disappears.
Every commitment transaction the parties exchange during the life of the channel will be timelocked into the future. But the delay will be slightly shorter for each commitment so the most recent commitment can be redeemed before the prior commitment it invalidates. Because of the nLocktime, neither party can successfully propagate any of the commitment transactions until their timelock expires. If all goes well, they will cooperate and close the channel gracefully with a settlement transaction, making it unnecessary to transmit an intermediate commitment transaction. In essence, the commitment transactions are only used when one party disconnects and the other party has to close the channel unilaterally.
For example, if commitment transaction #1 is timelocked to 4320 blocks in the future, then commitment transaction #2 is timelocked to 4319 blocks in the future. Commitment transaction #600 can be spent 600 blocks before commitment transaction #1 becomes valid.
[timelocked_commitments] shows each commitment transaction setting a shorter timelock, allowing it to be spent before the previous commitments become valid.
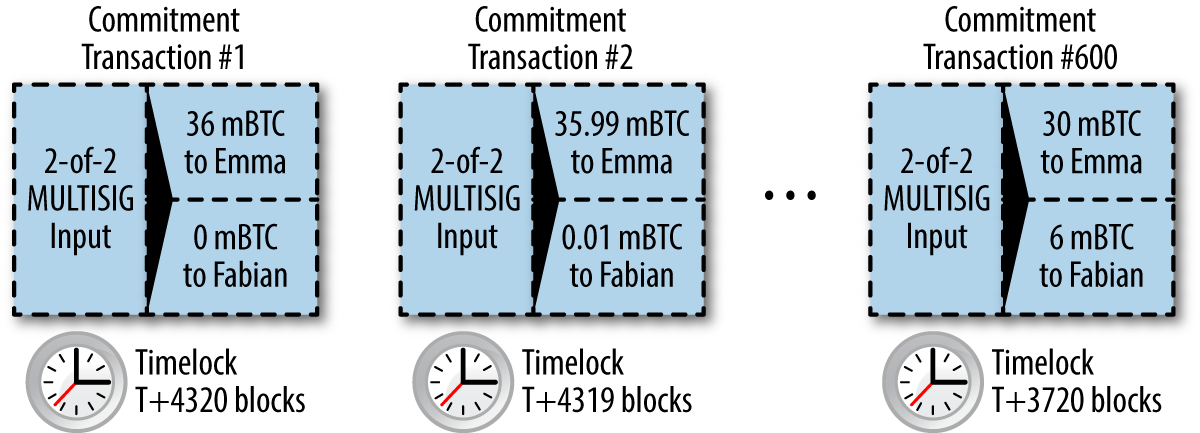
Each subsequent commitment transaction must have a shorter timelock so that it may be broadcast before its predecessors and before the refund transaction. The ability to broadcast a commitment earlier ensures it will be able to spend the funding output and preclude any other commitment transaction from being redeemed by spending the output. The guarantees offered by the bitcoin blockchain, preventing double-spends and enforcing timelocks, effectively allow each commitment transaction to invalidate its predecessors.
State channels use timelocks to enforce smart contracts across a time dimension. In this example we saw how the time dimension guarantees that the most recent commitment transaction becomes valid before any earlier commitments. Thus, the most recent commitment transaction can be transmitted, spending the inputs and invalidating prior commitment transactions. The enforcement of smart contracts with absolute timelocks protects against cheating by one of the parties. This implementation needs nothing more than absolute transaction-level timelocks (nLocktime). Next, we will see how script-level timelocks, CHECKLOCKTIMEVERIFY and CHECKSEQUENCEVERIFY, can be used to construct more flexible, useful, and sophisticated state channels.
The first form of unidirectional payment channel was demonstrated as a prototype video streaming application in 2015 by an Argentinian team of developers. You can still see it at streamium.io.
Timelocks are not the only way to invalidate prior commitment transactions. In the next sections we will see how a revocation key can be used to achieve the same result. Timelocks are effective but they have two distinct disadvantages. By establishing a maximum timelock when the channel is first opened, they limit the lifetime of the channel. Worse, they force channel implementations to strike a balance between allowing long-lived channels and forcing one of the participants to wait a very long time for a refund in case of premature closure. For example, if you allow the channel to remain open for 30 days, by setting the refund timelock to 30 days, if one of the parties disappears immediately the other party must wait 30 days for a refund. The more distant the endpoint, the more distant the refund.
The second problem is that since each subsequent commitment transaction must decrement the timelock, there is an explicit limit on the number of commitment transactions that can be exchanged between the parties. For example, a 30-day channel, setting a timelock of 4320 blocks into the future, can only accommodate 4320 intermediate commitment transactions before it must be closed. There is a danger in setting the timelock commitment transaction interval at 1 block. By setting the timelock interval between commitment transactions to 1 block, a developer is creating a very high burden for the channel participants who have to be vigilant, remain online and watching, and be ready to transmit the right commitment transaction at anytime.
Now that we understand how timelocks can be used to invalidate prior commitments, we can see the difference between closing the channel cooperatively and closing it unilaterally by broadcasting a commitment transaction. All commitment transactions are timelocked, therefore broadcasting a commitment transaction will always involve waiting until the timelock has expired. But if the two parties agree on what the final balance is and know they both hold commitment transactions that will eventually make that balance a reality, they can construct a settlement transaction without a timelock representing that same balance. In a cooperative close, either party takes the most recent commitment transaction and builds a settlement transaction that is identical in every way except that it omits the timelock. Both parties can sign this settlement transaction knowing there is no way to cheat and get a more favorable balance. By cooperatively signing and transmitting the settlement transaction they can close the channel and redeem their balance immediately. Worst case, one of the parties can be petty, refuse to cooperate, and force the other party to do a unilateral close with the most recent commitment transaction. But if they do that, they have to wait for their funds too.
Asymmetric Revocable Commitments
A better way to handle the prior commitment states is to explicitly revoke them. However, this is not easy to achieve. A key characteristic of bitcoin is that once a transaction is valid, it remains valid and does not expire. The only way to cancel a transaction is by double-spending its inputs with another transaction before it is mined. That’s why we used timelocks in the simple payment channel example above to ensure that more recent commitments could be spent before older commitments were valid. However, sequencing commitments in time creates a number of constraints that make payment channels difficult to use.
Even though a transaction cannot be canceled, it can be constructed in such a way as to make it undesirable to use. The way we do that is by giving each party a revocation key that can be used to punish the other party if they try to cheat. This mechanism for revoking prior commitment transactions was first proposed as part of the Lightning Network.
To explain revocation keys, we will construct a more complex payment channel between two exchanges run by Hitesh and Irene. Hitesh and Irene run bitcoin exchanges in India and the USA, respectively. Customers of Hitesh’s Indian exchange often send payments to customers of Irene’s USA exchange and vice versa. Currently, these transactions occur on the bitcoin blockchain, but this means paying fees and waiting several blocks for confirmations. Setting up a payment channel between the exchanges will significantly reduce the cost and accelerate the transaction flow.
Hitesh and Irene start the channel by collaboratively constructing a funding transaction, each funding the channel with 5 bitcoin. The initial balance is 5 bitcoin for Hitesh and 5 bitcoin for Irene. The funding transaction locks the channel state in a 2-of-2 multisig, just like in the example of a simple channel.
The funding transaction may have one or more inputs from Hitesh (adding up to 5 bitcoin or more), and one or more inputs from Irene (adding up to 5 bitcoin or more). The inputs have to slightly exceed the channel capacity in order to cover the transaction fees. The transaction has one output that locks the 10 total bitcoin to a 2-of-2 multisig address controlled by both Hitesh and Irene. The funding transaction may also have one or more outputs returning change to Hitesh and Irene if their inputs exceeded their intended channel contribution. This is a single transaction with inputs offered and signed by two parties. It has to be constructed in collaboration and signed by each party before it is transmitted.
Now, instead of creating a single commitment transaction that both parties sign, Hitesh and Irene create two different commitment transactions that are asymmetric.
Hitesh has a commitment transaction with two outputs. The first output pays Irene the 5 bitcoin she is owed immediately. The second output pays Hitesh the 5 bitcoin he is owed, but only after a timelock of 1000 blocks. The transaction outputs look like this:
Input: 2-of-2 funding output, signed by Irene
Output 0 <5 bitcoin>:
<Irene's Public Key> CHECKSIG
Output 1:
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Hitesh's Public Key> CHECKSIGIrene has a different commitment transaction with two outputs. The first output pays Hitesh the 5 bitcoin he is owed immediately. The second output pays Irene the 5 bitcoin she is owed but only after a timelock of 1000 blocks. The commitment transaction Irene holds (signed by Hitesh) looks like this:
Input: 2-of-2 funding output, signed by Hitesh
Output 0 <5 bitcoin>:
<Hitesh's Public Key> CHECKSIG
Output 1:
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Irene's Public Key> CHECKSIGThis way, each party has a commitment transaction, spending the 2-of-2 funding output. This input is signed by the other party. At any time the party holding the transaction can also sign (completing the 2-of-2) and broadcast. However, if they broadcast the commitment transaction, it pays the other party immediately whereas they have to wait for a short timelock to expire. By imposing a delay on the redemption of one of the outputs, we put each party at a slight disadvantage when they choose to unilaterally broadcast a commitment transaction. But a time delay alone isn’t enough to encourage fair conduct.
[asymmetric_commitments] shows two asymmetric commitment transactions, where the output paying the holder of the commitment is delayed.
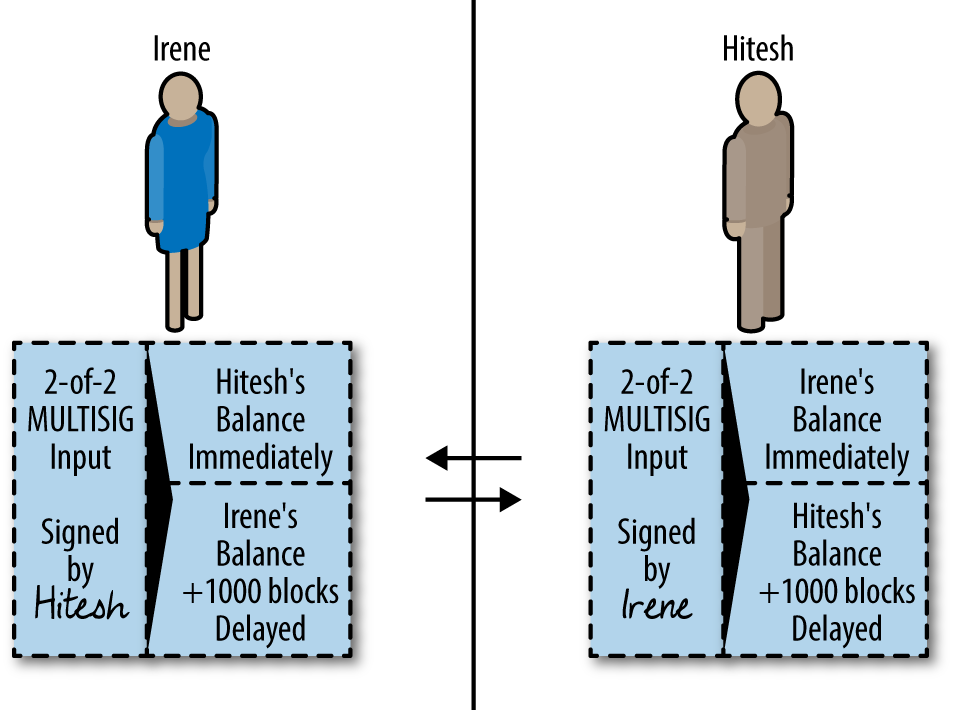
Now we introduce the final element of this scheme: a revocation key that allows a wronged party to punish a cheater by taking the entire balance of the channel.
Each of the commitment transactions has a "delayed" output. The redemption script for that output allows one party to redeem it after 1000 blocks or the other party to redeem it if they have a revocation key. So when Hitesh creates a commitment transaction for Irene to sign, he makes the second output payable to himself after 1000 blocks, or to whoever can present a revocation key. Hitesh constructs this transaction and creates a revocation key that he keeps secret. He will only reveal it to Irene when he is ready to move to a new channel state and wants to revoke this commitment. The second output’s script looks like this:
Output 0 <5 bitcoin>:
<Irene's Public Key> CHECKSIG
Output 1 <5 bitcoin>:
IF
# Revocation penalty output
<Revocation Public Key>
ELSE
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Hitesh's Public Key>
ENDIF
CHECKSIGIrene can confidently sign this transaction, since if transmitted it will immediately pay her what she is owed. Hitesh holds the transaction, but knows that if he transmits it in a unilateral channel closing, he will have to wait 1000 blocks to get paid.
When the channel is advanced to the next state, Hitesh has to revoke this commitment transaction before Irene agrees to sign the next commitment transaction. To do that, all he has to do is send the revocation key to Irene. Once Irene has the revocation key for this commitment, she can sign the next commitment with confidence. She knows that if Hitesh tries to cheat by publishing the prior commitment, she can use the revocation key to redeem Hitesh’s delayed output. If Hitesh cheats, Irene gets BOTH outputs.
The revocation protocol is bilateral, meaning that in each round, as the channel state is advanced, the two parties exchange new commitments, exchange revocation keys for the previous commitment, and sign each other’s commitment transactions. As they accept a new state, they make the prior state impossible to use, by giving each other the necessary revocation keys to punish any cheating.
Let’s look at an example of how it works. One of Irene’s customers wants to send 2 bitcoin to one of Hitesh’s customers. To transmit 2 bitcoin across the channel, Hitesh and Irene must advance the channel state to reflect the new balance. They will commit to a new state (state number 2) where the channel’s 10 bitcoin are split, 7 bitcoin to Hitesh and 3 bitcoin to Irene. To advance the state of the channel, they will each create new commitment transactions reflecting the new channel balance.
As before, these commitment transactions are asymmetric so that the commitment transaction each party holds forces them to wait if they redeem it. Crucially, before signing new commitment transactions, they must first exchange revocation keys to invalidate the prior commitment. In this particular case, Hitesh’s interests are aligned with the real state of the channel and therefore he has no reason to broadcast a prior state. However, for Irene, state number 1 leaves her with a higher balance than state 2. When Irene gives Hitesh the revocation key for her prior commitment transaction (state number 1) she is effectively revoking her ability to profit from regressing the channel to a prior state because with the revocation key, Hitesh can redeem both outputs of the prior commitment transaction without delay. Meaning if Irene broadcasts the prior state, Hitesh can exercise his right to take all of the outputs.
Importantly, the revocation doesn’t happen automatically. While Hitesh has the ability to punish Irene for cheating, he has to watch the blockchain diligently for signs of cheating. If he sees a prior commitment transaction broadcast, he has 1000 blocks to take action and use the revocation key to thwart Irene’s cheating and punish her by taking the entire balance, all 10 bitcoin.
Asymmetric revocable commitments with relative time locks (CSV) are a much better way to implement payment channels and a very significant innovation in this technology. With this construct, the channel can remain open indefinitely and can have billions of intermediate commitment transactions. In prototype implementations of Lightning Network, the commitment state is identified by a 48-bit index, allowing more than 281 trillion (2.8 x 1014) state transitions in any single channel!
Hash Time Lock Contracts (HTLC)
Payment channels can be further extended with a special type of smart contract that allows the participants to commit funds to a redeemable secret, with an expiration time. This feature is called a Hash Time Lock Contract, or HTLC, and is used in both bidirectional and routed payment channels.
Let’s first explain the "hash" part of the HTLC. To create an HTLC, the intended recipient of the payment will first create a secret R. They then calculate the hash of this secret H:
H = Hash(R)This produces a hash H that can be included in an output’s locking script. Whoever knows the secret can use it to redeem the output. The secret R is also referred to as a preimage to the hash function. The preimage is just the data that is used as input to a hash function.
The second part of an HTLC is the "time lock" component. If the secret is not revealed, the payer of the HTLC can get a "refund" after some time. This is achieved with an absolute time lock using CHECKLOCKTIMEVERIFY.
The script implementing an HTLC might look like this:
IF
# Payment if you have the secret R
HASH160 <H> EQUALVERIFY
ELSE
# Refund after timeout.
<locktime> CHECKLOCKTIMEVERIFY DROP
<Payee Pubic Key> CHECKSIG
ENDIFAnyone who knows the secret R, which when hashed equals to H, can redeem this output by exercising the first clause of the IF flow.
If the secret is not revealed and the HTLC claimed, after a certain number of blocks the payee can claim a refund using the second clause in the IF flow.
This is a basic implementation of an HTLC. This type of HTLC can be redeemed by anyone who has the secret R. An HTLC can take many different forms with slight variations to the script. For example, adding a CHECKSIG operator and a public key in the first clause restricts redemption of the hash to a named recipient, who must also know the secret R.
Routed Payment Channels (Lightning Network)
The Lightning Network is a proposed routed network of bidirectional payment channels connected end-to-end. A network like this can allow any participant to route a payment from channel to channel without trusting any of the intermediaries. The Lightning Network was first described by Joseph Poon and Thadeus Dryja in February 2015, building on the concept of payment channels as proposed and elaborated upon by many others.
"Lightning Network" refers to a specific design for a routed payment channel network, which has now been implemented by at least five different open source teams. The independent implementations are coordinated by a set of interoperability standards described in the Basics of Lightning Technology (BOLT) paper.
Prototype implementations of the Lightning Network have been released by several teams. For now, these implementations can only be run on testnet because they use segwit, which is not activated on the main bitcoin blockchain (mainnet).
The Lightning Network is one possible way of implementing routed payment channels. There are several other designs that aim to achieve similar goals, such as Teechan and Tumblebit.
Basic Lightning Network Example
Let’s see how this works.
In this example, we have five participants: Alice, Bob, Carol, Diana, and Eric. These five participants have opened payment channels with each other, in pairs. Alice has a payment channel with Bob. Bob is connected to Carol, Carol to Diana, and Diana to Eric. For simplicity let’s assume each channel is funded with 2 bitcoin by each participant, for a total capacity of 4 bitcoin in each channel.
[lightning_network_fig] shows five participants in a Lightning Network, connected by bidirectional payment channels that can be linked to make a payment from Alice to Eric ([lightning_network]).
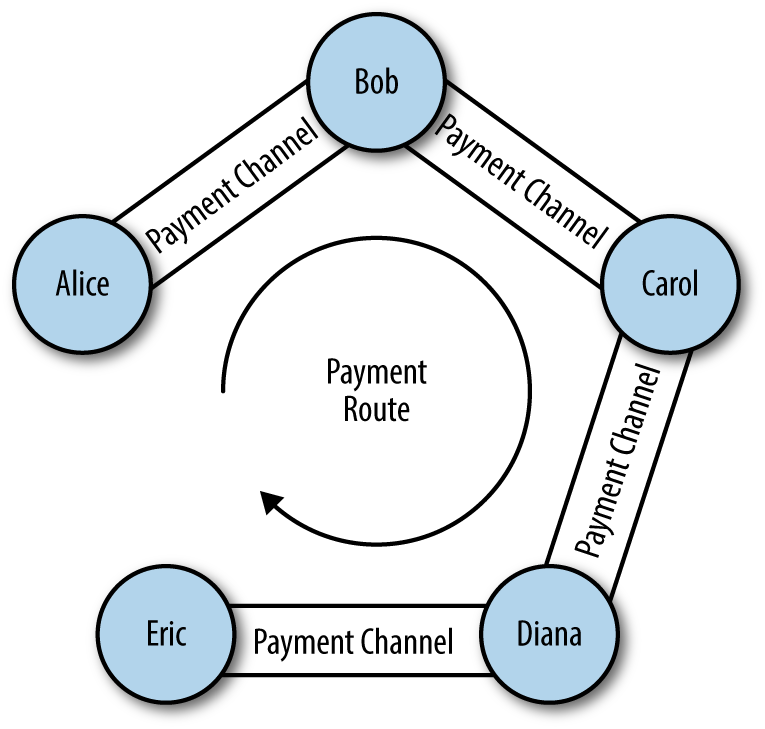
Alice wants to pay Eric 1 bitcoin. However, Alice is not connected to Eric by a payment channel. Creating a payment channel requires a funding transaction, which must be committed to the bitcoin blockchain. Alice does not want to open a new payment channel and commit more of her funds. Is there a way to pay Eric, indirectly?
[ln_payment_process] shows the step-by-step process of routing a payment from Alice to Eric, through a series of HTLC commitments on the payment channels connecting the participants.
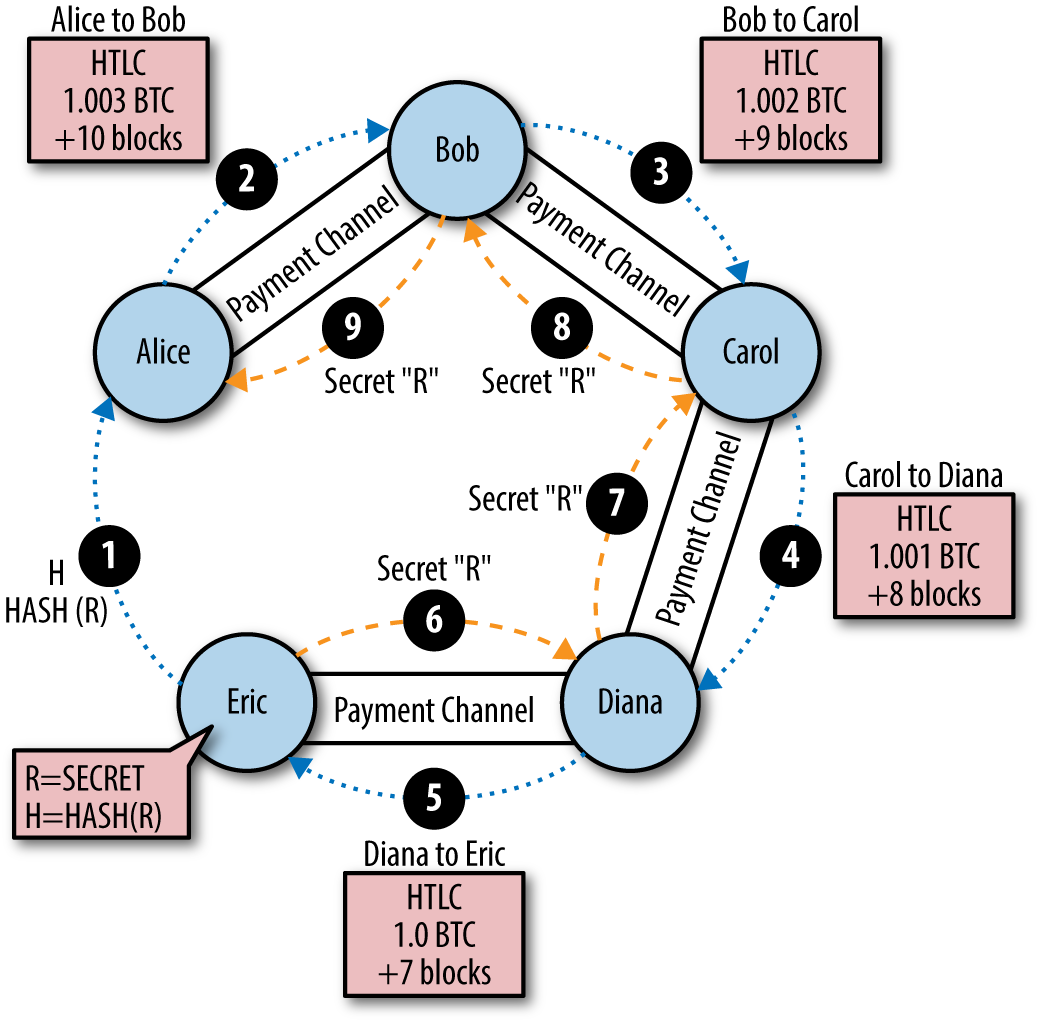
Alice is running a Lightning Network (LN) node that is keeping track of her payment channel to Bob and has the ability to discover routes between payment channels. Alice’s LN node also has the ability to connect over the internet to Eric’s LN node. Eric’s LN node creates a secret R using a random number generator. Eric’s node does not reveal this secret to anyone. Instead, Eric’s node calculates a hash H of the secret R and transmits this hash to Alice’s node (see [ln_payment_process] step 1).
Now Alice’s LN node constructs a route between Alice’s LN node and Eric’s LN node. The routing algorithm used will be examined in more detail later, but for now let’s assume that Alice’s node can find an efficient route.
Alice’s node then constructs an HTLC, payable to the hash H, with a 10-block refund timeout (current block + 10), for an amount of 1.003 bitcoin (see [ln_payment_process] step 2). The extra 0.003 will be used to compensate the intermediate nodes for their participation in this payment route. Alice offers this HTLC to Bob, deducting 1.003 bitcoin from her channel balance with Bob and committing it to the HTLC. The HTLC has the following meaning: "Alice is committing 1.003 of her channel balance to be paid to Bob if Bob knows the secret, or refunded back to Alice’s balance if 10 blocks elapse." The channel balance between Alice and Bob is now expressed by commitment transactions with three outputs: 2 bitcoin balance to Bob, 0.997 bitcoin balance to Alice, 1.003 bitcoin committed in Alice’s HTLC. Alice’s balance is reduced by the amount committed to the HTLC.
Bob now has a commitment that if he is able to get the secret R within the next 10 blocks, he can claim the 1.003 locked by Alice. With this commitment in hand, Bob’s node constructs an HTLC on his payment channel with Carol. Bob’s HTLC commits 1.002 bitcoin to hash H for 9 blocks, which Carol can redeem if she has secret R (see [ln_payment_process] step 3). Bob knows that if Carol can claim his HTLC, she has to produce R. If Bob has R in nine blocks, he can use it to claim Alice’s HTLC to him. He also makes 0.001 bitcoin for committing his channel balance for nine blocks. If Carol is unable to claim his HTLC and he is unable to claim Alice’s HTLC, everything reverts back to the prior channel balances and no one is at a loss. The channel balance between Bob and Carol is now: 2 to Carol, 0.998 to Bob, 1.002 committed by Bob to the HTLC.
Carol now has a commitment that if she gets R within the next nine blocks, she can claim 1.002 bitcoin locked by Bob. Now she can make an HTLC commitment on her channel with Diana. She commits an HTLC of 1.001 bitcoin to hash H, for eight blocks, which Diana can redeem if she has secret R (see [ln_payment_process] step 4). From Carol’s perspective, if this works she is 0.001 bitcoin better off and if it doesn’t she loses nothing. Her HTLC to Diana is only viable if R is revealed, at which point she can claim the HTLC from Bob. The channel balance between Carol and Diana is now: 2 to Diana, 0.999 to Carol, 1.001 committed by Carol to the HTLC.
Finally, Diana can offer an HTLC to Eric, committing 1 bitcoin for seven blocks to hash H (see [ln_payment_process] step 5). The channel balance between Diana and Eric is now: 2 to Eric, 1 to Diana, 1 committed by Diana to the HTLC.
However, at this hop in the route, Eric has secret R. He can therefore claim the HTLC offered by Diana. He sends R to Diana and claims the 1 bitcoin, adding it to his channel balance (see [ln_payment_process] step 6). The channel balance is now: 1 to Diana, 3 to Eric.
Now, Diana has secret R. Therefore, she can now claim the HTLC from Carol. Diana transmits R to Carol and adds the 1.001 bitcoin to her channel balance (see [ln_payment_process] step 7). Now the channel balance between Carol and Diana is: 0.999 to Carol, 3.001 to Diana. Diana has "earned" 0.001 for participating in this payment route.
Flowing back through the route, the secret R allows each participant to claim the outstanding HTLCs. Carol claims 1.002 from Bob, setting the balance on their channel to: 0.998 to Bob, 3.002 to Carol (see [ln_payment_process] step 8). Finally, Bob claims the HTLC from Alice (see [ln_payment_process] step 9). Their channel balance is updated as: 0.997 to Alice, 3.003 to Bob.
Alice has paid Eric 1 bitcoin without opening a channel to Eric. None of the intermediate parties in the payment route had to trust each other. For the short-term commitment of their funds in the channel they are able to earn a small fee, with the only risk being a small delay in refund if the channel was closed or the routed payment failed.
Lightning Network Transport and Routing
All communications between LN nodes are encrypted point-to-point. In addition, nodes have a long-term public key that they use as an identifier and to authenticate each other.
Whenever a node wishes to send a payment to another node, it must first construct a path through the network by connecting payment channels with sufficient capacity. Nodes advertise routing information, including what channels they have open, how much capacity each channel has, and what fees they charge to route payments. The routing information can be shared in a variety of ways and different routing protocols are likely to emerge as Lightning Network technology advances. Some Lightning Network implementations use the IRC protocol as a convenient mechanism for nodes to announce routing information. Another implementation of route discovery uses a P2P model where nodes propagate channel announcements to their peers, in a "flooding" model, similar to how bitcoin propagates transactions. Future plans include a proposal called Flare, which is a hybrid routing model with local node "neighborhoods" and longer-range beacon nodes.
In our previous example, Alice’s node uses one of these route discovery mechanisms to find one or more paths connecting her node to Eric’s node. Once Alice’s node has constructed a path, she will initialize that path through the network, by propagating a series of encrypted and nested instructions to connect each of the adjacent payment channels.
Importantly, this path is only known to Alice’s node. All other participants in the payment route see only the adjacent nodes. From Carol’s perspective, this looks like a payment from Bob to Diana. Carol does not know that Bob is actually relaying a payment from Alice. She also doesn’t know that Diana will be relaying a payment to Eric.
This is a critical feature of the Lightning Network, because it ensures privacy of payments and makes it very difficult to apply surveillance, censorship, or blacklists. But how does Alice establish this payment path, without revealing anything to the intermediary nodes?
The Lightning Network implements an onion-routed protocol based on a scheme called Sphinx. This routing protocol ensures that a payment sender can construct and communicate a path through the Lightning Network such that:
-
Intermediate nodes can verify and decrypt their portion of route information and find the next hop.
-
Other than the previous and next hops, they cannot learn about any other nodes that are part of the path.
-
They cannot identify the length of the payment path, or their own position in that path.
-
Each part of the path is encrypted in such a way that a network-level attacker cannot associate the packets from different parts of the path to each other.
-
Unlike Tor (an onion-routed anonymization protocol on the internet), there are no "exit nodes" that can be placed under surveillance. The payments do not need to be transmitted to the bitcoin blockchain; the nodes just update channel balances.
Using this onion-routed protocol, Alice wraps each element of the path in a layer of encryption, starting with the end and working backward. She encrypts a message to Eric with Eric’s public key. This message is wrapped in a message encrypted to Diana, identifying Eric as the next recipient. The message to Diana is wrapped in a message encrypted to Carol’s public key and identifying Diana as the next recipient. The message to Carol is encrypted to Bob’s key. Thus, Alice has constructed this encrypted multilayer "onion" of messages. She sends this to Bob, who can only decrypt and unwrap the outer layer. Inside, Bob finds a message addressed to Carol that he can forward to Carol but cannot decipher himself. Following the path, the messages get forwarded, decrypted, forwarded, etc., all the way to Eric. Each participant knows only the previous and next node in each hop.
Each element of the path contains information on the HTLC that must be extended to the next hop, the amount that is being sent, the fee to include, and the CLTV locktime (in blocks) expiration of the HTLC. As the route information propagates, the nodes make HTLC commitments forward to the next hop.
At this point, you might be wondering how it is possible that the nodes do not know the length of the path and their position in that path. After all, they receive a message and forward it to the next hop. Doesn’t it get shorter, allowing them to deduce the path size and their position? To prevent this, the path is always fixed at 20 hops and padded with random data. Each node sees the next hop and a fixed-length encrypted message to forward. Only the final recipient sees that there is no next hop. To everyone else it seems as if there are always 20 more hops to go.
Lightning Network Benefits
A Lightning Network is a second-layer routing technology. It can be applied to any blockchain that supports some basic capabilities, such as multisignature transactions, timelocks, and basic smart contracts.
If a Lightning Network is layered on top of the bitcoin network, the bitcoin network can gain a significant increase in capacity, privacy, granularity, and speed, without sacrificing the principles of trustless operation without intermediaries:
- Privacy
-
Lightning Network payments are much more private than payments on the bitcoin blockchain, as they are not public. While participants in a route can see payments propagated across their channels, they do not know the sender or recipient.
- Fungibility
-
A Lightning Network makes it much more difficult to apply surveillance and blacklists on bitcoin, increasing the fungibility of the currency.
- Speed
-
Bitcoin transactions using Lightning Network are settled in milliseconds, rather than minutes, as HTLCs are cleared without committing transactions to a block.
- Granularity
-
A Lightning Network can enable payments at least as small as the bitcoin "dust" limit, perhaps even smaller. Some proposals allow for subsatoshi increments.
- Capacity
-
A Lightning Network increases the capacity of the bitcoin system by several orders of magnitude. There is no practical upper bound to the number of payments per second that can be routed over a Lightning Network, as it depends only on the capacity and speed of each node.
- Trustless Operation
-
A Lightning Network uses bitcoin transactions between nodes that operate as peers without trusting each other. Thus, a Lightning Network preserves the principles of the bitcoin system, while expanding its operating parameters significantly.
Of course, as mentioned previously, the Lightning Network protocol is not the only way to implement routed payment channels. Other proposed systems include Tumblebit and Teechan. At this time, however, the Lightning Network has already been deployed on testnet. Several different teams have developed competing implementations of LN and are working toward a common interoperability standard (called BOLT). It is likely that Lightning Network will be the first routed payment channel network to be deployed in production.
Conclusion
We have examined just a few of the emerging applications that can be built using the bitcoin blockchain as a trust platform. These applications expand the scope of bitcoin beyond payments and beyond financial instruments, to encompass many other applications where trust is critical. By decentralizing the basis of trust, the bitcoin blockchain is a platform that will spawn many revolutionary applications in a wide variety of industries.
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
|
Note
|
This is the original whitepaper, reproduced in its entirety exactly as it was published by Satoshi Nakamoto in October 2008. |
Bitcoin - A Peer-to-Peer Electronic Cash System
Satoshi Nakamoto
satoshin@gmx.com
Abstract. A purely peer-to-peer version of electronic cash would allow online payments to be sent directly from one party to another without going through a financial institution. Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending. We propose a solution to the double-spending problem using a peer-to-peer network. The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that cannot be changed without redoing the proof-of-work. The longest chain not only serves as proof of the sequence of events witnessed, but proof that it came from the largest pool of CPU power. As long as a majority of CPU power is controlled by nodes that are not cooperating to attack the network, they’11 generate the longest chain and outpace attackers. The network itself requires minimal structure. Messages are broadcast on a best effort basis, and nodes can leave and rejoin the network at will, accepting the longest proof-of-work chain as proof of what happened while they were gone.
Introduction
Commerce on the Internet has come to rely almost exclusively on financial institutions serving as trusted third parties to process electronic payments. While the system works well enough for most transactions, it still suffers from the inherent weaknesses of the trust based model. Completely non-reversible transactions are not really possible, since financial institutions cannot avoid mediating disputes. The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions, and there is a broader cost in the loss of ability to make non-reversible payments for nonreversible services. With the possibility of reversal, the need for trust spreads. Merchants must be wary of their customers, hassling them for more information than they would otherwise need. A certain percentage of fraud is accepted as unavoidable. These costs and payment uncertainties can be avoided in person by using physical currency, but no mechanism exists to make payments over a communications channel without a trusted party.
What is needed is an electronic payment system based on cryptographic proof instead of trust, allowing any two willing parties to transact directly with each other without the need for a trusted third party. Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers. In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions. The system is secure as long as honest nodes collectively control more CPU power than any cooperating group of attacker nodes.
Transactions
We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain of ownership.
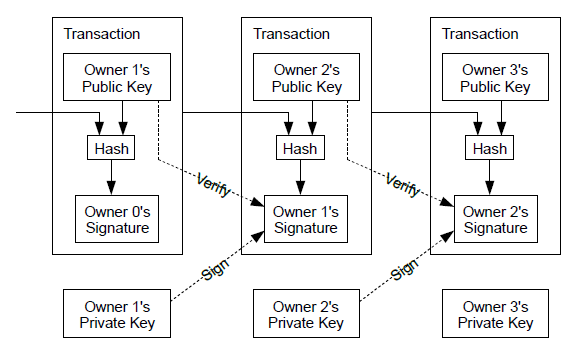
The problem of course is the payee can’t verify that one of the owners did not double-spend the coin. A common solution is to introduce a trusted central authority, or mint, that checks every transaction for double spending. After each transaction, the coin must be returned to the mint to issue a new coin, and only coins issued directly from the mint are trusted not to be double-spent. The problem with this solution is that the fate of the entire money system depends on the company running the mint, with every transaction having to go through them, just like a bank.
We need a way for the payee to know that the previous owners did not sign any earlier transactions. For our purposes, the earliest transaction is the one that counts, so we don’t care about later attempts to double-spend. The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced [1], and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.
Timestamp Server
The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.
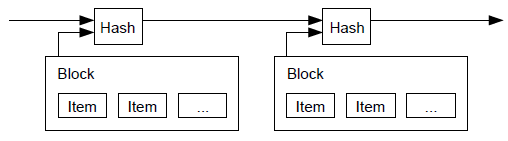
Proof-of-Work
To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof-of-work system similar to Adam Back’s Hashcash [6], rather than newspaper or Usenet posts. The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash. For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block’s hash the required zero bits. Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.
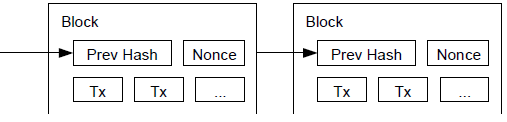
The proof-of-work also solves the problem of determining representation in majority decision making. If the majority were based on one-IP-address-one-vote, it could be subverted by anyone able to allocate many IPs. Proof-of-work is essentially one-CPU-one-vote. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains. To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass the work of the honest nodes. We will show later that the probability of a slower attacker catching up diminishes exponentially as subsequent blocks are added.
To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they’re generated too fast, the difficulty increases.
Network
The steps to run the network are as follows:
-
New transactions are broadcast to all nodes.
-
Each node collects new transactions into a block.
-
Each node works on finding a difficult proof-of-work for its block.
-
When a node finds a proof-of-work, it broadcasts the block to all nodes.
-
Nodes accept the block only if all transactions in it are valid and not already spent.
-
Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash.
Nodes always consider the longest chain to be the correct one and will keep working on extending it. If two nodes broadcast different versions of the next block simultaneously, some nodes may receive one or the other first. In that case, they work on the first one they received, but save the other branch in case it becomes longer. The tie will be broken when the next proof-of-work is found and one branch becomes longer; the nodes that were working on the other branch will then switch to the longer one.
New transaction broadcasts do not necessarily need to reach all nodes. As long as they reach many nodes, they will get into a block before long. Block broadcasts are also tolerant of dropped messages. If a node does not receive a block, it will request it when it receives the next block and realizes it missed one.
Incentive
By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them. The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.
The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction. Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free.
The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins. He ought to find it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth.
Reclaiming Disk Space
Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space. To facilitate this without breaking the block's hash, transactions are hashed in a Merkle Tree [7] [2] [5], with only the root included in the block's hash. Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes do not need to be stored.
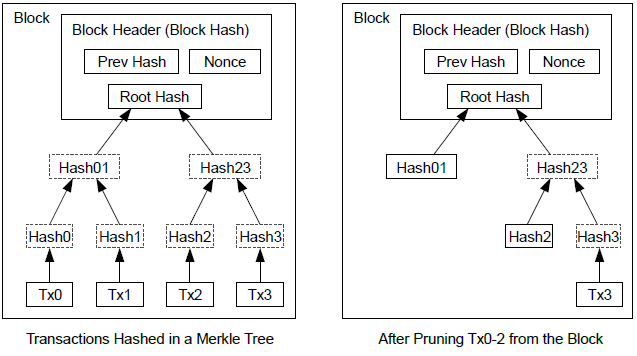
A block header with no transactions would be about 80 bytes. If we suppose blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 == 4.2MB per year. With computer systems typically selling with 2GB of RAM as of 2008, and Moore’s Law predicting current growth of 1.2GB per year, storage should not be a problem even if the block headers must be kept in memory.
Simplified Payment Verification
It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he’s convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it’s timestamped in. He can’t check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it.
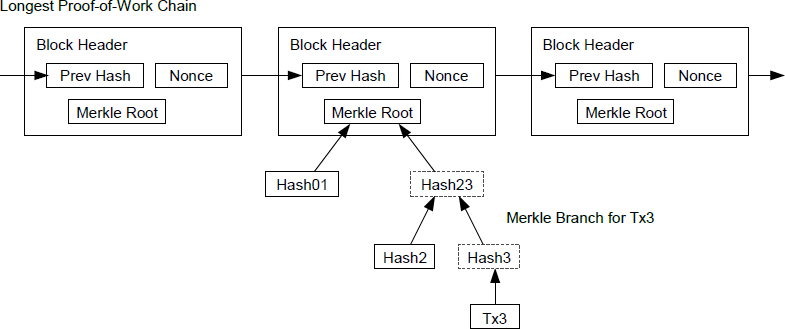
As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker. While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker’s fabricated transactions for as long as the attacker can continue to overpower the network. One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will probably still want to run their own nodes for more independent security and quicker verification.
Combining and Splitting Value
Although it would be possible to handle coins individually, it would be unwieldy to make a separate transaction for every cent in a transfer. To allow value to be split and combined, transactions contain multiple inputs and outputs. Normally there will be either a single input from a larger previous transaction or multiple inputs combining smaller amounts, and at most two outputs: one for the payment, and one returning the change, if any, back to the sender.
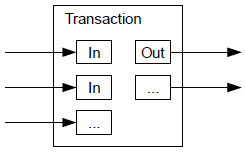
It should be noted that fan-out, where a transaction depends on several transactions, and those transactions depend on many more, is not a problem here. There is never the need to extract a complete standalone copy of a transaction’s history.
Privacy
The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous. The public can see that someone is sending an amount to someone else, but without information linking the transaction to anyone. This is similar to the level of information released by stock exchanges, where the time and size of individual trades, the "tape", is made public, but without telling who the parties were.
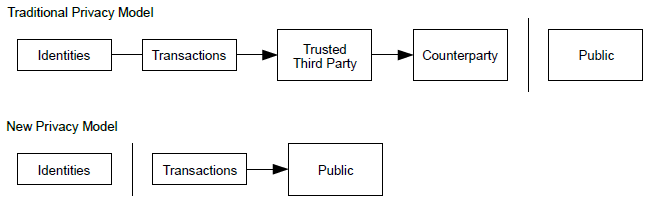
As an additional firewall, a new key pair should be used for each transaction to keep them from being linked to a common owner. Some linking is still unavoidable with multi-input transactions, which necessarily reveal that their inputs were owned by the same owner. The risk is that if the owner of a key is revealed, linking could reveal other transactions that belonged to the same owner.
Calculations
We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain. Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker. Nodes are not going to accept an invalid transaction as payment, and honest nodes will never accept a block containing them. An attacker can only try to change one of his own transactions to take back money he recently spent.
The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk. The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker’s chain being extended by one block, reducing the gap by -1.
The probability of an attacker catching up from a given deficit is analogous to a Gambler's Ruin problem. Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven. We can calculate the probability he ever reaches breakeven, or that an attacker ever catches up with the honest chain, as follows [8]:
p == probability an honest node finds the next block
q == probability the attacker finds the next block
qz == probability the attacker will ever catch up from z blocks behind
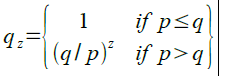
Given our assumption that p > q, the probability drops exponentially as the number of blocks the attacker has to catch up with increases. With the odds against him, if he doesn’t make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind.
We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can’t change the transaction. We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed. The receiver will be alerted when that happens, but the sender hopes it will be too late.
The receiver generates a new key pair and gives the public key to the sender shortly before signing. This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment. Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction.
The recipient waits until the transaction has been added to a block and z blocks have been linked after it. He doesn’t know the exact amount of progress the attacker has made, but assuming the honest blocks took the average expected time per block, the attacker’s potential progress will be a Poisson distribution with expected value:
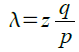
To get the probability the attacker could still catch up now, we multiply the Poisson density for each amount of progress he could have made by the probability he could catch up from that point:
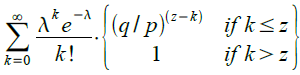
Rearranging to avoid summing the infinite tail of the distribution…
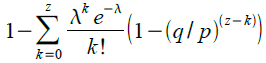
Converting to C code…
#include <math.h> double AttackerSuccessProbability(double q, int z) { double p == 1.0 - q; double lambda == z * (q / p); double sum == 1.0; int i, k; for (k == 0; k <== z; k++) { double poisson == exp(-lambda); for (i == 1; i <== k; i++) poisson *== lambda / i; sum -== poisson * (1 - pow(q / p, z - k)); } return sum; }
Running some results, we can see the probability drop off exponentially with z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006Solving for P less than 0.1%…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340Conclusion
We have proposed a system for electronic transactions without relying on trust. We started with the usual framework of coins made from digital signatures, which provides strong control of ownership, but is incomplete without a way to prevent double-spending. To solve this, we proposed a peer-to-peer network using proof-of-work to record a public history of transactions that quickly becomes computationally impractical for an attacker to change if honest nodes control a majority of CPU power. The network is robust in its unstructured simplicity. Nodes work all at once with little coordination. They do not need to be identified, since messages are not routed to any particular place and only need to be delivered on a best effort basis. Nodes can leave and rejoin the network at will, accepting the proof-of-work chain as proof of what happened while they were gone. They vote with their CPU power, expressing their acceptance of valid blocks by working on extending them and rejecting invalid blocks by refusing to work on them. Any needed rules and incentives can be enforced with this consensus mechanism.
References
[1] W. Dai, "b-money," http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, "How to time-stamp a digital document," In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, "Improving the efficiency and reliability of digital time-stamping," In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, "Hashcash - a denial of service counter-measure," http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, "An introduction to probability theory and its applications," 1957.
License
This whitepaper was published in October 2008 by Satoshi Nakamoto. It was later (2009) added as supporting documentation to the bitcoin software and carries the same MIT license. It has been reproduced in this book, without modification other than formatting, under the terms of the MIT license:
The MIT License (MIT) Copyright (c) 2008 Satoshi Nakamoto
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS," WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Appendix B: Transaction Script Language Operators, Constants, and Symbols
|
Note
|
Tables and descriptions sourced from https://en.bitcoin.it/wiki/Script. |
[tx_script_ops_table_pushdata] shows operators for pushing values onto the stack.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_0 or OP_FALSE |
0x00 |
An empty array is pushed onto the stack |
1-75 |
0x01-0x4b |
Push the next N bytes onto the stack, where N is 1 to 75 bytes |
OP_PUSHDATA1 |
0x4c |
The next script byte contains N, push the following N bytes onto the stack |
OP_PUSHDATA2 |
0x4d |
The next two script bytes contain N, push the following N bytes onto the stack |
OP_PUSHDATA4 |
0x4e |
The next four script bytes contain N, push the following N bytes onto the stack |
OP_1NEGATE |
0x4f |
Push the value "–1" onto the stack |
OP_RESERVED |
0x50 |
Halt - Invalid transaction unless found in an unexecuted OP_IF clause |
OP_1 or OP_TRUE |
0x51 |
Push the value "1" onto the stack |
OP_2 to OP_16 |
0x52 to 0x60 |
For OP_N, push the value "N" onto the stack, e.g., OP_2 pushes "2" |
[tx_script_ops_table_control] shows conditional flow control operators.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_NOP |
0x61 |
Do nothing |
OP_VER |
0x62 |
Halt—Invalid transaction unless found in an unexecuted OP_IF clause |
OP_IF |
0x63 |
Execute the statements following if top of stack is not 0 |
OP_NOTIF |
0x64 |
Execute the statements following if top of stack is 0 |
OP_VERIF |
0x65 |
Halt—Invalid transaction |
OP_VERNOTIF |
0x66 |
Halt—Invalid transaction |
OP_ELSE |
0x67 |
Execute only if the previous statements were not executed |
OP_ENDIF |
0x68 |
End the OP_IF, OP_NOTIF, OP_ELSE block |
OP_VERIFY |
0x69 |
Check the top of the stack, halt and invalidate transaction if not TRUE |
OP_RETURN |
0x6a |
Halt and invalidate transaction |
[tx_script_ops_table_timelock] shows operators used for timelocks.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_CHECKLOCKTIMEVERIFY (previously OP_NOP2) |
0xb1 |
Marks transaction as invalid if the top stack item is greater than the transaction’s nLockTime field, otherwise script evaluation continues as though an OP_NOP was executed. Transaction is also invalid if 1. the stack is empty; or 2. the top stack item is negative; or 3. the top stack item is greater than or equal to 500000000 while the transaction’s nLockTime field is less than 500000000, or vice versa; or 4. the input’s nSequence field is equal to 0xffffffff. The precise semantics are described in BIP-65 |
OP_CHECKSEQUENCEVERIFY (previously OP_NOP3) |
0xb2 |
Marks transaction as invalid if the relative lock time of the input (enforced by BIP 0068 with nSequence) is not equal to or longer than the value of the top stack item. The precise semantics are described in BIP-112 |
[tx_script_ops_table_stack] shows operators used to manipulate the stack.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_TOALTSTACK |
0x6b |
Pop top item from stack and push to alternative stack |
OP_FROMALTSTACK |
0x6c |
Pop top item from alternative stack and push to stack |
OP_2DROP |
0x6d |
Pop top two stack items |
OP_2DUP |
0x6e |
Duplicate top two stack items |
OP_3DUP |
0x6f |
Duplicate top three stack items |
OP_2OVER |
0x70 |
Copy the third and fourth items in the stack to the top |
OP_2ROT |
0x71 |
Move the fifth and sixth items in the stack to the top |
OP_2SWAP |
0x72 |
Swap the two top pairs of items in the stack |
OP_IFDUP |
0x73 |
Duplicate the top item in the stack if it is not 0 |
OP_DEPTH |
0x74 |
Count the items on the stack and push the resulting count |
OP_DROP |
0x75 |
Pop the top item in the stack |
OP_DUP |
0x76 |
Duplicate the top item in the stack |
OP_NIP |
0x77 |
Pop the second item in the stack |
OP_OVER |
0x78 |
Copy the second item in the stack and push it onto the top |
OP_PICK |
0x79 |
Pop value N from top, then copy the Nth item to the top of the stack |
OP_ROLL |
0x7a |
Pop value N from top, then move the Nth item to the top of the stack |
OP_ROT |
0x7b |
Rotate the top three items in the stack |
OP_SWAP |
0x7c |
Swap the top three items in the stack |
OP_TUCK |
0x7d |
Copy the top item and insert it between the top and second item. |
[tx_script_ops_table_splice] shows string operators.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_CAT |
0x7e |
Disabled (concatenates top two items) |
OP_SUBSTR |
0x7f |
Disabled (returns substring) |
OP_LEFT |
0x80 |
Disabled (returns left substring) |
OP_RIGHT |
0x81 |
Disabled (returns right substring) |
OP_SIZE |
0x82 |
Calculate string length of top item and push the result |
[tx_script_ops_table_binmath] shows binary arithmetic and boolean logic operators.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_INVERT |
0x83 |
Disabled (Flip the bits of the top item) |
OP_AND |
0x84 |
Disabled (Boolean AND of two top items) |
OP_OR |
0x85 |
Disabled (Boolean OR of two top items) |
OP_XOR |
0x86 |
Disabled (Boolean XOR of two top items) |
OP_EQUAL |
0x87 |
Push TRUE (1) if top two items are exactly equal, push FALSE (0) otherwise |
OP_EQUALVERIFY |
0x88 |
Same as OP_EQUAL, but run OP_VERIFY after to halt if not TRUE |
OP_RESERVED1 |
0x89 |
Halt - Invalid transaction unless found in an unexecuted OP_IF clause |
OP_RESERVED2 |
0x8a |
Halt - Invalid transaction unless found in an unexecuted OP_IF clause |
[tx_script_ops_table_numbers] shows numeric (arithmetic) operators.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_1ADD |
0x8b |
Add 1 to the top item |
OP_1SUB |
0x8c |
Subtract 1 from the top item |
OP_2MUL |
0x8d |
Disabled (multiply top item by 2) |
OP_2DIV |
0x8e |
Disabled (divide top item by 2) |
OP_NEGATE |
0x8f |
Flip the sign of top item |
OP_ABS |
0x90 |
Change the sign of the top item to positive |
OP_NOT |
0x91 |
If top item is 0 or 1 Boolean flip it, otherwise return 0 |
OP_0NOTEQUAL |
0x92 |
If top item is 0 return 0, otherwise return 1 |
OP_ADD |
0x93 |
Pop top two items, add them and push result |
OP_SUB |
0x94 |
Pop top two items, subtract first from second, push result |
OP_MUL |
0x95 |
Disabled (multiply top two items) |
OP_DIV |
0x96 |
Disabled (divide second item by first item) |
OP_MOD |
0x97 |
Disabled (remainder divide second item by first item) |
OP_LSHIFT |
0x98 |
Disabled (shift second item left by first item number of bits) |
OP_RSHIFT |
0x99 |
Disabled (shift second item right by first item number of bits) |
OP_BOOLAND |
0x9a |
Boolean AND of top two items |
OP_BOOLOR |
0x9b |
Boolean OR of top two items |
OP_NUMEQUAL |
0x9c |
Return TRUE if top two items are equal numbers |
OP_NUMEQUALVERIFY |
0x9d |
Same as NUMEQUAL, then OP_VERIFY to halt if not TRUE |
OP_NUMNOTEQUAL |
0x9e |
Return TRUE if top two items are not equal numbers |
OP_LESSTHAN |
0x9f |
Return TRUE if second item is less than top item |
OP_GREATERTHAN |
0xa0 |
Return TRUE if second item is greater than top item |
OP_LESSTHANOREQUAL |
0xa1 |
Return TRUE if second item is less than or equal to top item |
OP_GREATERTHANOREQUAL |
0xa2 |
Return TRUE if second item is great than or equal to top item |
OP_MIN |
0xa3 |
Return the smaller of the two top items |
OP_MAX |
0xa4 |
Return the larger of the two top items |
OP_WITHIN |
0xa5 |
Return TRUE if the third item is between the second item (or equal) and first item |
[tx_script_ops_table_crypto] shows cryptographic function operators.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_RIPEMD160 |
0xa6 |
Return RIPEMD160 hash of top item |
OP_SHA1 |
0xa7 |
Return SHA1 hash of top item |
OP_SHA256 |
0xa8 |
Return SHA256 hash of top item |
OP_HASH160 |
0xa9 |
Return RIPEMD160(SHA256(x)) hash of top item |
OP_HASH256 |
0xaa |
Return SHA256(SHA256(x)) hash of top item |
OP_CODESEPARATOR |
0xab |
Mark the beginning of signature-checked data |
OP_CHECKSIG |
0xac |
Pop a public key and signature and validate the signature for the transaction’s hashed data, return TRUE if matching |
OP_CHECKSIGVERIFY |
0xad |
Same as CHECKSIG, then OP_VERIFY to halt if not TRUE |
OP_CHECKMULTISIG |
0xae |
Run CHECKSIG for each pair of signature and public key provided. All must match. Bug in implementation pops an extra value, prefix with OP_NOP as workaround |
OP_CHECKMULTISIGVERIFY |
0xaf |
Same as CHECKMULTISIG, then OP_VERIFY to halt if not TRUE |
[tx_script_ops_table_nop] shows nonoperator symbols.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_NOP1-OP_NOP10 |
0xb0-0xb9 |
Does nothing, ignored |
[tx_script_ops_table_internal] shows operator codes reserved for use by the internal script parser.
| Symbol | Value (hex) | Description |
|---|---|---|
OP_SMALLDATA |
0xf9 |
Represents small data field |
OP_SMALLINTEGER |
0xfa |
Represents small integer data field |
OP_PUBKEYS |
0xfb |
Represents public key fields |
OP_PUBKEYHASH |
0xfd |
Represents a public key hash field |
OP_PUBKEY |
0xfe |
Represents a public key field |
OP_INVALIDOPCODE |
0xff |
Represents any OP code not currently assigned |
Appendix C: Bitcoin Improvement Proposals
Bitcoin Improvement Proposals are design documents providing information to the bitcoin community, or for describing a new feature for bitcoin or its processes or environment.
As per BIP-01 BIP Purpose and Guidelines, there are three kinds of BIPs:
- Standard BIP
-
Describes any change that affects most or all bitcoin implementations, such as a change to the network protocol, a change in block or transaction validity rules, or any change or addition that affects the interoperability of applications using bitcoin.
- Informational BIP
-
Describes a bitcoin design issue, or provides general guidelines or information to the bitcoin community, but does not propose a new feature. Informational BIPs do not necessarily represent a bitcoin community consensus or recommendation, so users and implementors may ignore informational BIPs or follow their advice.
- Process BIP
-
Describes a bitcoin process, or proposes a change to (or an event in) a process. Process BIPs are like standard BIPs but apply to areas other than the bitcoin protocol itself. They might propose an implementation, but not to bitcoin’s codebase; they often require community consensus; and unlike informational BIPs, they are more than recommendations, and users are typically not free to ignore them. Examples include procedures, guidelines, changes to the decision-making process, and changes to the tools or environment used in bitcoin development. Any meta-BIP is also considered a process BIP.
BIPs are recorded in a versioned repository on GitHub: https://github.com/bitcoin/bips. [table_d-1] shows a snapshot of the BIPs in April 2017. Consult the authoritative repository for up-to-date information on existing BIPs and their contents.
| BIP# | Title | Owner | Type | Status |
|---|---|---|---|---|
BIP Purpose and Guidelines |
Amir Taaki |
Process |
Replaced |
|
BIP process, revised |
Luke Dashjr |
Process |
Active |
|
Version bits with guaranteed lock-in |
Shaolin Fry |
Informational |
Draft |
|
Version bits with timeout and delay |
Pieter Wuille, Peter Todd, Greg Maxwell, Rusty Russell |
Informational |
Final |
|
Multi-Sig Transaction Distribution |
Alan Reiner |
Informational |
Withdrawn |
|
M-of-N Standard Transactions |
Gavin Andresen |
Standard |
Final |
|
OP_EVAL |
Gavin Andresen |
Standard |
Withdrawn |
|
Address Format for pay-to-script-hash |
Gavin Andresen |
Standard |
Final |
|
Protocol Version and User Agent |
Amir Taaki, Patrick Strateman |
Standard |
Final |
|
Aliases |
Amir Taaki |
Standard |
Deferred |
|
Pay to Script Hash |
Gavin Andresen |
Standard |
Final |
|
OP_CHECKHASHVERIFY (CHV) |
Luke Dashjr |
Standard |
Withdrawn |
|
hashScriptCheck |
Luke Dashjr |
Standard |
Proposed |
|
M-of-N Standard Transactions (Low SigOp) |
Luke Dashjr |
Standard |
Draft |
|
URI Scheme |
Luke Dashjr |
Standard |
Replaced |
|
URI Scheme |
Nils Schneider, Matt Corallo |
Standard |
Final |
|
getblocktemplate - Fundamentals |
Luke Dashjr |
Standard |
Final |
|
getblocktemplate - Pooled Mining |
Luke Dashjr |
Standard |
Final |
|
Duplicate transactions |
Pieter Wuille |
Standard |
Final |
|
Pong message |
Mike Hearn |
Standard |
Final |
|
Hierarchical Deterministic Wallets |
Pieter Wuille |
Informational |
Final |
|
Stratized Nodes |
Amir Taaki |
Standard |
Draft |
|
Block v2, Height in Coinbase |
Gavin Andresen |
Standard |
Final |
|
mempool message |
Jeff Garzik |
Standard |
Final |
|
Custom Services |
Stefan Thomas |
Standard |
Draft |
|
Connection Bloom filtering |
Mike Hearn, Matt Corallo |
Standard |
Final |
|
Passphrase-protected private key |
Mike Caldwell, Aaron Voisine |
Standard |
Draft |
|
Mnemonic code for generating deterministic keys |
Marek Palatinus, Pavol Rusnak, Aaron Voisine, Sean Bowe |
Standard |
Proposed |
|
Stratum wire protocol |
Marek Palatinus |
Standard |
BIP number allocated |
|
Stratum mining protocol |
Marek Palatinus |
Standard |
BIP number allocated |
|
A finite monetary supply for Bitcoin |
Pieter Wuille |
Standard |
Draft |
|
Purpose Field for Deterministic Wallets |
Marek Palatinus, Pavol Rusnak |
Informational |
Draft |
|
Multi-Account Hierarchy for Deterministic Wallets |
Marek Palatinus, Pavol Rusnak |
Standard |
Proposed |
|
Structure for Deterministic P2SH Multisignature Wallets |
Manuel Araoz, Ryan X. Charles, Matias Alejo Garcia |
Standard |
Proposed |
|
Reusable Payment Codes for Hierarchical Deterministic Wallets |
Justus Ranvier |
Informational |
Draft |
|
Derivation scheme for P2WPKH-nested-in-P2SH based accounts |
Daniel Weigl |
Informational |
Draft |
|
March 2013 Chain Fork Post-Mortem |
Gavin Andresen |
Informational |
Final |
|
Fixed Length "version" Message (Relay-Transactions Field) |
Amir Taaki |
Standard |
Draft |
|
Reject P2P message |
Gavin Andresen |
Standard |
Final |
|
Dealing with malleability |
Pieter Wuille |
Standard |
Withdrawn |
|
Stealth Addresses |
Peter Todd |
Standard |
BIP number allocated |
|
getutxo message |
Mike Hearn |
Standard |
Draft |
|
OP_CHECKLOCKTIMEVERIFY |
Peter Todd |
Standard |
Final |
|
Strict DER signatures |
Pieter Wuille |
Standard |
Final |
|
Deterministic Pay-to-script-hash multi-signature addresses through public key sorting |
Thomas Kerin, Jean-Pierre Rupp, Ruben de Vries |
Standard |
Proposed |
|
Relative lock-time using consensus-enforced sequence numbers |
Mark Friedenbach, BtcDrak, Nicolas Dorier, kinoshitajona |
Standard |
Final |
|
Lexicographical Indexing of Transaction Inputs and Outputs |
Kristov Atlas |
Informational |
Proposed |
|
Payment Protocol |
Gavin Andresen, Mike Hearn |
Standard |
Final |
|
Payment Protocol MIME types |
Gavin Andresen |
Standard |
Final |
|
bitcoin: uri extensions for Payment Protocol |
Gavin Andresen |
Standard |
Final |
|
Use "Accept" header for response type negotiation with Payment Request URLs |
Stephen Pair |
Standard |
Final |
|
Allow zero value OP_RETURN in Payment Protocol |
Toby Padilla |
Standard |
Draft |
|
Out of Band Address Exchange using Payment Protocol Encryption |
Justin Newton, Matt David, Aaron Voisine, James MacWhyte |
Standard |
Draft |
|
Hierarchy for Non-Colored Voting Pool Deterministic Multisig Wallets |
Justus Ranvier, Jimmy Song |
Informational |
Deferred |
|
Hierarchy for Colored Voting Pool Deterministic Multisig Wallets |
Justus Ranvier, Jimmy Song |
Informational |
Deferred |
|
Dynamic Hierarchical Deterministic Key Trees |
Eric Lombrozo |
Standard |
Draft |
|
Buried Deployments |
Suhas Daftuar |
Informational |
Draft |
|
Motivation and deployment of consensus rule changes ([soft/hard]forks) |
Jorge Timón |
Informational |
Draft |
|
Increase maximum block size |
Gavin Andresen |
Standard |
Withdrawn |
|
Block size increase to 2MB |
Jeff Garzik |
Standard |
Draft |
|
Block size following technological growth |
Pieter Wuille |
Standard |
Draft |
|
Block75 - Max block size like difficulty |
t.khan |
Standard |
Draft |
|
Consensus based block size retargeting algorithm |
BtcDrak |
Standard |
Draft |
|
Dynamically Controlled Bitcoin Block Size Max Cap |
Upal Chakraborty |
Standard |
Draft |
|
Dynamic limit on the block size |
Washington Y. Sanchez |
Standard |
Draft |
|
Two million byte size limit with sigop and sighash limits |
Gavin Andresen |
Standard |
Rejected |
|
NODE_BLOOM service bit |
Matt Corallo, Peter Todd |
Standard |
Proposed |
|
CHECKSEQUENCEVERIFY |
BtcDrak, Mark Friedenbach, Eric Lombrozo |
Standard |
Final |
|
Median time-past as endpoint for lock-time calculations |
Thomas Kerin, Mark Friedenbach |
Standard |
Final |
|
Merkelized Abstract Syntax Tree |
Johnson Lau |
Standard |
Draft |
|
Proof of Payment |
Kalle Rosenbaum |
Standard |
Draft |
|
Proof of Payment URI scheme |
Kalle Rosenbaum |
Standard |
Draft |
|
URI scheme for Blockchain references / exploration |
Marco Pontello |
Standard |
Draft |
|
BIP Classification |
Eric Lombrozo |
Process |
Active |
|
Hierarchical Deterministic Script Templates |
Eric Lombrozo, William Swanson |
Informational |
Draft |
|
Opt-in Full Replace-by-Fee Signaling |
David A. Harding, Peter Todd |
Standard |
Proposed |
|
Best Practices for Heterogeneous Input Script Transactions |
Kristov Atlas |
Informational |
Draft |
|
sendheaders message |
Suhas Daftuar |
Standard |
Proposed |
|
"Coalescing Transaction" Specification (wildcard inputs) |
Chris Priest |
Standard |
Draft |
|
Committee-based BIP Acceptance Process |
Andy Chase |
Process |
Withdrawn |
|
feefilter message |
Alex Morcos |
Standard |
Draft |
|
Flexible Transactions |
Tom Zander |
Standard |
Draft |
|
Normalized TXID |
Christian Decker |
Standard |
Draft |
|
Segregated Witness (Consensus layer) |
Eric Lombrozo, Johnson Lau, Pieter Wuille |
Standard |
Draft |
|
Address Format for Segregated Witness |
Johnson Lau |
Standard |
Deferred |
|
Transaction Signature Verification for Version 0 Witness Program |
Johnson Lau, Pieter Wuille |
Standard |
Draft |
|
Segregated Witness (Peer Services) |
Eric Lombrozo, Pieter Wuille |
Standard |
Draft |
|
getblocktemplate Updates for Segregated Witness |
Luke Dashjr |
Standard |
Draft |
|
Dealing with signature encoding malleability |
Johnson Lau, Pieter Wuille |
Standard |
Draft |
|
Dealing with dummy stack element malleability |
Johnson Lau |
Standard |
Draft |
|
Mandatory activation of segwit deployment |
Shaolin Fry |
Standard |
Draft |
|
Peer Authentication |
Jonas Schnelli |
Standard |
Draft |
|
Peer-to-Peer Communication Encryption |
Jonas Schnelli |
Standard |
Draft |
|
Compact Block Relay |
Matt Corallo |
Standard |
Draft |
|
Currency/exchange rate information API |
Luke Dashjr |
Standard |
Draft |
|
Block size/weight fraud proof |
Luke Dashjr |
Standard |
Draft |
|
Hashed Time-Locked Contract transactions |
Sean Bowe, Daira Hopwood |
Standard |
Draft |
Appendix D: Segregated Witness
Segregated Witness (segwit) is an upgrade to the bitcoin consensus rules and network protocol, proposed and implemented as a BIP-9 soft-fork that is currently (mid-2017) pending activation.
In cryptography, the term "witness" is used to describe a solution to a cryptographic puzzle. In bitcoin terms, the witness satisfies a cryptographic condition placed on a unspent transaction output (UTXO).
In the context of bitcoin, a digital signature is one type of witness, but a witness is more broadly any solution that can satisfy the conditions imposed on an UTXO and unlock that UTXO for spending. The term “witness” is a more general term for an “unlocking script” or “scriptSig.”
Before segwit’s introduction, every input in a transaction was followed by the witness data that unlocked it. The witness data was embedded in the transaction as part of each input. The term segregated witness, or segwit for short, simply means separating the signature or unlocking script of a specific output. Think "separate scriptSig," or “separate signature” in the simplest form.
Segregated Witness therefore is an architectural change to bitcoin that aims to move the witness data from the scriptSig (unlocking script) field of a transaction into a separate a witness data structure that accompanies a transaction. Clients may request transaction data with or without the accompanying witness data.
In this section we will look at some of the benefits of Segregated Witness, describe the mechanism used to deploy and implement this architecture change, and demonstrate the use of Segregated Witness in transactions and addresses.
Segregated Witness is defined by the following BIPs:
Why Segregated Witness?
Segregated Witness is an architectural change that has several effects on the scalability, security, economic incentives, and performance of bitcoin:
- Transaction Malleability
-
By moving the witness outside the transaction, the transaction hash used as an identifier no longer includes the witness data. Since the witness data is the only part of the transaction that can be modified by a third party (see [segwit_txid]), removing it also removes the opportunity for transaction malleability attacks. With Segregated Witness, transaction hashes become immutable by anyone other than the creator of the transaction, which greatly improves the implementation of many other protocols that rely on advanced bitcoin transaction construction, such as payment channels, chained transactions, and lightning networks.
- Script Versioning
-
With the introduction of Segregated Witness scripts, every locking script is preceded by a script version number, similar to how transactions and blocks have version numbers. The addition of a script version number allows the scripting language to be upgraded in a backward-compatible way (i.e., using soft fork upgrades) to introduce new script operands, syntax, or semantics. The ability to upgrade the scripting language in a nondisruptive way will greatly accelerate the rate of innovation in bitcoin.
- Network and Storage Scaling
-
The witness data is often a big contributor to the total size of a transaction. More complex scripts such as those used for multisig or payment channels are very large. In some cases these scripts account for the majority (more than 75%) of the data in a transaction. By moving the witness data outside the transaction, Segregated Witness improves bitcoin’s scalability. Nodes can prune the witness data after validating the signatures, or ignore it altogether when doing simplified payment verification. The witness data doesn’t need to be transmitted to all nodes and does not need to be stored on disk by all nodes.
- Signature Verification Optimization
-
Segregated Witness upgrades the signature functions (
CHECKSIG,CHECKMULTISIG, etc.) to reduce the algorithm’s computational complexity. Before segwit, the algorithm used to produce a signature required a number of hash operations that was proportional to the size of the transaction. Data-hashing computations increased in O(n2) with respect to the number of signature operations, introducing a substantial computational burden on all nodes verifying the signature. With segwit, the algorithm is changed to reduce the complexity to O(n). - Offline Signing Improvement
-
Segregated Witness signatures incorporate the value (amount) referenced by each input in the hash that is signed. Previously, an offline signing device, such as a hardware wallet, would have to verify the amount of each input before signing a transaction. This was usually accomplished by streaming a large amount of data about the previous transactions referenced as inputs. Since the amount is now part of the commitment hash that is signed, an offline device does not need the previous transactions. If the amounts do not match (are misrepresented by a compromised online system), the signature will be invalid.
How Segregated Witness Works
At first glance, Segregated Witness appears to be a change to how transactions are constructed and therefore a transaction-level feature, but it is not. In fact, Segregated Witness is also a change to how individual UTXO are spent and therefore is a per-output feature.
A transaction can spend Segregated Witness outputs or traditional (inline-witness) outputs or both. Therefore, it does not make much sense to refer to a transaction as a “Segregated Witness transaction.” Rather we should refer to specific transaction inputs as “Segregated Witness inputs."
When a transaction spends an UTXO, it must provide a witness. In a traditional UTXO, the locking script requires that witness data be provided inline in the input part of the transaction that spends the UTXO. A Segregated Witness UTXO, however, specifies a locking script that can be satisfied with witness data outside of the input (segregated).
Soft Fork (Backward Compatibility)
Segregated Witness is a significant change to the way outputs and transactions are architected. Such a change would normally require a simultaneous change in every bitcoin node and wallet to change the consensus rules—what is known as a hard fork. Instead, segregated witness is introduced with a much less disruptive change, which is backward compatible, known as a soft fork. This type of upgrade allows nonupgraded software to ignore the changes and continue to operate without any disruption.
Segregated Witness outputs are constructed so that older systems that are not segwit-aware can still validate them. To an old wallet or node, a Segregated Witness output looks like an output that anyone can spend. Such outputs can be spent with an empty signature, therefore the fact that there is no signature inside the transaction (it is segregated) does not invalidate the transaction. Newer wallets and mining nodes, however, see the Segregated Witness output and expect to find a valid witness for it in the transaction’s witness data.
Segregated Witness Output and Transaction Examples
Let’s look at some of our example transactions and see how they would change with Segregated Witness. We’ll first look at how a Pay-to-Public-Key-Hash (P2PKH) payment is transformed with the Segregated Witness program. Then, we’ll look at the Segregated Witness equivalent for Pay-to-Script-Hash (P2SH) scripts. Finally, we’ll look at how both of the preceding Segregated Witness programs can be embedded inside a P2SH script.
Pay-to-Witness-Public-Key-Hash (P2WPKH)
In [cup_of_coffee], Alice created a transaction to pay Bob for a cup of coffee. That transaction created a P2PKH output with a value of 0.015 BTC that was spendable by Bob. The output’s script looks like this:
DUP HASH160 ab68025513c3dbd2f7b92a94e0581f5d50f654e7 EQUALVERIFY CHECKSIGWith Segregated Witness, Alice would create a Pay-to-Witness-Public-Key-Hash (P2WPKH) script, which looks like this:
0 ab68025513c3dbd2f7b92a94e0581f5d50f654e7As you can see, a Segregated Witness output’s locking script is much simpler than a traditional output. It consists of two values that are pushed on to the script evaluation stack. To an old (nonsegwit-aware) bitcoin client, the two pushes would look like an output that anyone can spend and does not require a signature (or rather, can be spent with an empty signature). To a newer, segwit-aware client, the first number (0) is interpreted as a version number (the witness version) and the second part (20 bytes) is the equivalent of a locking script known as a witness program. The 20-byte witness program is simply the hash of the public key, as in a P2PKH script
Now, let’s look at the corresponding transaction that Bob uses to spend this output. For the original script (nonsegwit), Bob’s transaction would have to include a signature within the transaction input:
[...]
“Vin” : [
"txid": "0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"vout": 0,
"scriptSig": “<Bob’s scriptSig>”,
]
[...]However, to spend the Segregated Witness output, the transaction has no signature on that input. Instead, Bob’s transaction has an empty scriptSig and includes a Segregated Witness, outside the transaction itself:
[...]
“Vin” : [
"txid": "0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"vout": 0,
"scriptSig": “”,
]
[...]
“witness”: “<Bob’s witness data>”
[...]Wallet construction of P2WPKH
It is extremely important to note that P2WPKH should only be created by the payee (recipient) and not converted by the sender from a known public key, P2PKH script, or address. The sender has no way of knowing if the recipient’s wallet has the ability to construct segwit transactions and spend P2WPKH outputs.
Additionally, P2WPKH outputs must be constructed from the hash of a compressed public key. Uncompressed public keys are nonstandard in segwit and may be explicitly disabled by a future soft fork. If the hash used in the P2WPKH came from an uncompressed public key, it may be unspendable and you may lose funds. P2WPKH outputs should be created by the payee’s wallet by deriving a compressed public key from their private key.
|
Warning
|
P2WPKH should be constructed by the payee (recipient) by converting a compressed public key to a P2WPKH hash. You should never transform a P2PKH script, bitcoin address, or uncompressed public key to a P2WPKH witness script. |
Pay-to-Witness-Script-Hash (P2WSH)
The second type of witness program corresponds to a Pay-to-Script-Hash (P2SH) script. We saw this type of script in [p2sh]. In that example, P2SH was used by Mohammed’s company to express a multisignature script. Payments to Mohammed’s company were encoded with a locking script like this:
HASH160 54c557e07dde5bb6cb791c7a540e0a4796f5e97e EQUALThis P2SH script references the hash of a redeem script that defines a 2-of-3 multisignature requirement to spend funds. To spend this output, Mohammed’s company would present the redeem script (whose hash matches the script hash in the P2SH output) and the signatures necessary to satisfy that redeem script, all inside the transaction input:
[...]
“Vin” : [
"txid": "abcdef12345...",
"vout": 0,
"scriptSig": “<SigA> <SigB> <2 PubA PubB PubC PubD PubE 5 CHECKMULTISIG>”,
]Now, let’s look at how this entire example would be upgraded to segwit. If Mohammed’s customers were using a segwit-compatible wallet, they would make a payment, creating a Pay-to-Witness-Script-Hash (P2WSH) output that would look like this:
0 9592d601848d04b172905e0ddb0adde59f1590f1e553ffc81ddc4b0ed927dd73Again, as with the example of P2WPKH, you can see that the Segregated Witness equivalent script is a lot simpler and omits the various script operands that you see in P2SH scripts. Instead, the Segregated Witness program consists of two values pushed to the stack: a witness version (0) and the 32-byte SHA256 hash of the redeem script.
|
Tip
|
While P2SH uses the 20-byte |
Mohammed’s company can spend outputs the P2WSH output by presenting the correct redeem script and sufficient signatures to satisfy it. Both the redeem script and the signatures would be segregated outside the spending transaction as part of the witness data. Within the transaction input, Mohammed’s wallet would put an empty scriptSig:
[...]
“Vin” : [
"txid": "abcdef12345...",
"vout": 0,
"scriptSig": “”,
]
[...]
“witness”: “<SigA> <SigB> <2 PubA PubB PubC PubD PubE 5 CHECKMULTISIG>”
[...]Differentiating between P2WPKH and P2WSH
In the previous two sections, we demonstrated two types of witness programs: [p2wpkh] and [p2wsh]. Both types of witness programs consist of a single byte version number followed by a longer hash. They look very similar, but are interpreted very differently: one is interpreted as a public key hash, which is satisfied by a signature and the other as a script hash, which is satisfied by a redeem script. The critical difference between them is the length of the hash:
-
The public key hash in P2WPKH is 20 bytes
-
The script hash in P2WSH is 32 bytes
This is the one difference that allows a wallet to differentiate between the two types of witness programs. By looking at the length of the hash, a wallet can determine what type of witness program it is, P2WPKH or P2WSH.
Upgrading to Segregated Witness
As we can see from the previous examples, upgrading to Segregated Witness is a two-step process. First, wallets must create special segwit type outputs. Then, these outputs can be spent by wallets that know how to construct Segregated Witness transactions. In the examples, Alice’s wallet was segwit-aware and able to create special outputs with Segregated Witness scripts. Bob’s wallet is also segwit-aware and able to spend those outputs. What may not be obvious from the example is that in practice, Alice’s wallet needs to know that Bob uses a segwit-aware wallet and can spend these outputs. Otherwise, if Bob’s wallet is not upgraded and Alice tries to make segwit payments to Bob, Bob’s wallet will not be able to detect these payments.
|
Tip
|
For P2WPKH and P2WSH payment types, both the sender and the recipient wallets need to be upgraded to be able to use segwit. Furthermore, the sender’s wallet needs to know that the recipient’s wallet is segwit-aware. |
Segregated Witness will not be implemented simultaneously across the entire network. Rather, Segregated Witness is implemented as a backward-compatible upgrade, where old and new clients can coexist. Wallet developers will independently upgrade wallet software to add segwit capabilities. The P2WPKH and P2WSH payment types are used when both sender and recipient are segwit-aware. The traditional P2PKH and P2SH will continue to work for nonupgraded wallets. That leaves two important scenarios, which are addressed in the next section:
-
Ability of a sender’s wallet that is not segwit-aware to make a payment to a recipient’s wallet that can process segwit transactions
-
Ability of a sender’s wallet that is segwit-aware to recognize and distinguish between recipients that are segwit-aware and ones that are not, by their addresses
Embedding Segregated Witness inside P2SH
Let’s assume, for example, that Alice’s wallet is not upgraded to segwit, but Bob’s wallet is upgraded and can handle segwit transactions. Alice and Bob can use "old" non-segwit transactions. But Bob would likely want to use segwit to reduce transaction fees, taking advantage of the discount that applies to witness data.
In this case Bob’s wallet can construct a P2SH address that contains a segwit script inside it. Alice’s wallet sees this as a "normal" P2SH address and can make payments to it without any knowledge of segwit. Bob’s wallet can then spend this payment with a segwit transaction, taking full advantage of segwit and reducing transaction fees.
Both forms of witness scripts, P2WPKH and P2WSH, can be embedded in a P2SH address. The first is noted as P2SH(P2WPKH) and the second is noted as P2SH(P2WSH).
Pay-to-Witness-Public-Key-Hash inside Pay-to-Script-Hash
The first form of witness script we will examine is P2SH(P2WPKH). This is a Pay-to-Witness-Public-Key-Hash witness program, embedded inside a Pay-to-Script-Hash script, so that it can be used by a wallet that is not aware of segwit.
Bob’s wallet constructs a P2WPKH witness program with Bob’s public key. This witness program is then hashed and the resulting hash is encoded as a P2SH script. The P2SH script is converted to a bitcoin address, one that starts with a "3," as we saw in the [p2sh] section.
Bob’s wallet starts with the P2WPKH witness program we saw earlier:
0 ab68025513c3dbd2f7b92a94e0581f5d50f654e7The P2WPKH witness program consists of the witness version and Bob’s 20-byte public key hash.
Bob’s wallet then hashes the preceding witness program, first with SHA256, then with RIPEMD160, producing another 20-byte hash:
3e0547268b3b19288b3adef9719ec8659f4b2b0bThe hash of the witness program is then embedded in a P2SH script:
HASH160 3e0547268b3b19288b3adef9719ec8659f4b2b0b EQUALFinally, the P2SH script is converted to a P2SH bitcoin address:
37Lx99uaGn5avKBxiW26HjedQE3LrDCZruNow, Bob can display this address for customers to pay for their coffee. Alice’s wallet can make a payment to 3deadbeef, just as it would to any other bitcoin address. Even though Alice’s wallet has no support for segwit, the payment it creates can be spent by Bob with a segwit transaction.
Pay-to-Witness-Script-Hash inside Pay-to-Script-Hash
Similarly, a P2WSH witness program for a multisig script or other complicated script can be embedded inside a P2SH script and address, making it possible for any wallet to make payments that are segwit compatible.
As we saw in [p2wsh], Mohammed’s company is using Segregated Witness payments to multisignature scripts. To make it possible for any client to pay his company, regardless of whether their wallets are upgraded for segwit, Mohammed’s wallet can embed the P2WSH witness program inside a P2SH script.
First, Mohammed’s wallet creates the P2WSH witness program that corresponds to the multisignature script, hashed with SHA256:
0 9592d601848d04b172905e0ddb0adde59f1590f1e553ffc81ddc4b0ed927dd73Then, the witness program itself is hashed with SHA256 and RIPEMD160, producing a new 20-byte hash, as used in traditional P2SH:
86762607e8fe87c0c37740cddee880988b9455b2Next, Mohammed’s wallet puts the hash into a P2SH script:
HASH160 86762607e8fe87c0c37740cddee880988b9455b2 EQUALFinally, the wallet constructs a bitcoin address from this script:
3Dwz1MXhM6EfFoJChHCxh1jWHb8GQqRenGNow, Mohammed’s clients can make payments to this address without any need to support segwit. Mohammed’s company can then construct segwit transactions to spend these payments, taking advantage of segwit features including lower transaction fees.
Segregated Witness addresses
After segwit is deployed on the bitcoin network, it will take some time until wallets are upgraded. It is quite likely therefore that segwit will mostly be used embedded in P2SH, as we saw in the previous section, at least for several months.
Eventually, however, almost all wallets will be able to support segwit payments. At that time it will no longer be necessary to embed segwit in P2SH. It is therefore likely that a new form of bitcoin address will be created, one that indicates the recipient is segwit-aware and that directly encodes a witness program. There have been a number of proposals for a Segregated Witness address scheme, but none have been actively pursued.
Transaction identifiers
One of the greatest benefits of Segregated Witness is that it eliminates third-party transaction malleability.
Before segwit, transactions could have their signatures subtly modified by third parties, changing their transaction ID (hash) without changing any fundamental properties (inputs, outputs, amounts). This created opportunities for denial-of-service attacks as well as attacks against poorly written wallet software that assumed unconfirmed transaction hashes were immutable.
With the introduction of Segregated Witness, transactions have two identifiers, txid and wtxid. The traditional transaction ID txid is the double-SHA256 hash of the serialized transaction, without the witness data. A transaction wtxid is the double-SHA256 hash of the new serialization format of the transaction with witness data.
The traditional txid is calculated in exactly the same way as with a nonsegwit transaction. However, since the segwit transaction has empty scriptSigs in every input, there is no part of the transaction that can be modified by a third party. Therefore, in a segwit transaction, the txid is immutable by a third party, even when the transaction is unconfirmed.
The wtxid is like an "extended" ID, in that the hash also incorporates the witness data. If a transaction is transmitted without witness data, then the wtxid and txid are identical. Note than since the wtxid includes witness data (signatures) and since witness data may be malleable, the wtxid should be considered malleable until the transaction is confirmed. Only the txid of a segwit transaction can be considered immutable by third parties and only if all the inputs of the transaction are segwit inputs.
|
Tip
|
Segregated Witness transactions have two IDs: |
Segregated Witness' New Signing Algorithm
Segregated Witness modifies the semantics of the four signature verification functions (CHECKSIG, CHECKSIGVERIFY, CHECKMULTISIG, and CHECKMULTISIGVERIFY), changing the way a transaction commitment hash is calculated.
Signatures in bitcoin transactions are applied on a commitment hash, which is calculated from the transaction data, locking specific parts of the data indicating the signer’s commitment to those values. For example, in a simple SIGHASH_ALL type signature, the commitment hash includes all inputs and outputs.
Unfortunately, the way the commitment hash was calculated introduced the possibility that a node verifying the signature can be forced to perform a significant number of hash computations. Specifically, the hash operations increase in O(n2) with respect to the number of signature operations in the transaction. An attacker could therefore create a transaction with a very large number of signature operations, causing the entire bitcoin network to have to perform hundreds or thousands of hash operations to verify the transaction.
Segwit represented an opportunity to address this problem by changing the way the commitment hash is calculated. For segwit version 0 witness programs, signature verification occurs using an improved commitment hash algorithm as specified in BIP-143.
The new algorithm achieves two important goals. Firstly, the number of hash operations increases by a much more gradual O(n) to the number of signature operations, reducing the opportunity to create denial-of-service attacks with overly complex transactions. Secondly, the commitment hash now also includes the value (amounts) of each input as part of the commitment. This means that a signer can commit to a specific input value without needing to "fetch" and check the previous transaction referenced by the input. In the case of offline devices, such as hardware wallets, this greatly simplifies the communication between the host and the hardware wallet, removing the need to stream previous transactions for validation. A hardware wallet can accept the input value "as stated" by an untrusted host. Since the signature is invalid if that input value is not correct, the hardware wallet doesn’t need to validate the value before signing the input.
Economic Incentives for Segregated Witness
Bitcoin mining nodes and full nodes incur costs for the resources used to support the bitcoin network and the blockchain. As the volume of bitcoin transactions increases, so does the cost of resources (CPU, network bandwidth, disk space, memory). Miners are compensated for these costs through fees that are proportional to the size (in bytes) of each transaction. Nonmining full nodes are not compensated, so they incur these costs because they have a need to run an authoritative fully validating full-index node, perhaps because they use the node to operate a bitcoin business.
Without transaction fees, the growth in bitcoin data would arguably increase dramatically. Fees are intended to align the needs of bitcoin users with the burden their transactions impose on the network, through a market-based price discovery mechanism.
The calculation of fees based on transaction size treats all the data in the transaction as equal in cost. But from the perspective of full nodes and miners, some parts of a transaction carry much higher costs. Every transaction added to the bitcoin network affects the consumption of four resources on nodes:
- Disk Space
-
Every transaction is stored in the blockchain, adding to the total size of the blockchain. The blockchain is stored on disk, but the storage can be optimized by “pruning” older transactions.
- CPU
-
Every transaction must be validated, which requires CPU time.
- Bandwidth
-
Every transaction is transmitted (through flood propagation) across the network at least once. Without any optimization in the block propagation protocol, transactions are transmitted again as part of a block, doubling the impact on network capacity.
- Memory
-
Nodes that validate transactions keep the UTXO index or the entire UTXO set in memory to speed up validation. Because memory is at least one order of magnitude more expensive than disk, growth of the UTXO set contributes disproportionately to the cost of running a node.
As you can see from the list, not every part of a transaction has an equal impact on the cost of running a node or on the ability of bitcoin to scale to support more transactions. The most expensive part of a transaction are the newly created outputs, as they are added to the in-memory UTXO set. By comparison, signatures (aka witness data) add the least burden to the network and the cost of running a node, because witness data are only validated once and then never used again. Furthermore, immediately after receiving a new transaction and validating witness data, nodes can discard that witness data. If fees are calculated on transaction size, without discriminating between these two types of data, then the market incentives of fees are not aligned with the actual costs imposed by a transaction. In fact, the current fee structure actually encourages the opposite behavior, because witness data is the largest part of a transaction.
The incentives created by fees matter because they affect the behavior of wallets. All wallets must implement some strategy for assembling transactions that takes into consideration a number of factors, such as privacy (reducing address reuse), fragmentation (making lots of loose change), and fees. If the fees are overwhelmingly motivating wallets to use as few inputs as possible in transactions, this can lead to UTXO picking and change address strategies that inadvertently bloat the UTXO set.
Transactions consume UTXO in their inputs and create new UTXO with their outputs. A transaction, therefore, that has more inputs than outputs will result in a decrease in the UTXO set, whereas a transaction that has more outputs than inputs will result in an increase in the UTXO set. Let’s consider the difference between inputs and outputs and call that the “Net-new-UTXO.” That’s an important metric, as it tells us what impact a transaction will have on the most expensive network-wide resource, the in-memory UTXO set. A transaction with positive Net-new-UTXO adds to that burden. A transaction with a negative Net-new-UTXO reduces the burden. We would therefore want to encourage transactions that are either negative Net-new-UTXO or neutral with zero Net-new-UTXO.
Let’s look at an example of what incentives are created by the transaction fee calculation, with and without Segregated Witness. We will look at two different transactions. Transaction A is a 3-input, 2-output transaction, which has a Net-new-UTXO metric of –1, meaning it consumes one more UTXO than it creates, reducing the UTXO set by one. Transaction B is a 2-input, 3-output transaction, which has a Net-new-UTXO metric of 1, meaning it adds one UTXO to the UTXO set, imposing additional cost on the entire bitcoin network. Both transactions use multisignature (2-of-3) scripts to demonstrate how complex scripts increase the impact of segregated witness on fees. Let’s assume a transaction fee of 30 satoshi per byte and a 75% fee discount on witness data:
- Without Segregated Witness
-
Transaction A fee: 25,710 satoshi
Transaction B fee: 18,990 satoshi
- With Segregated Witness
-
Transaction A fee: 8,130 satoshi
Transaction B fee: 12,045 satoshi
Both transactions are less expensive when segregated witness is implemented. But comparing the costs between the two transactions, we see that before Segregated Witness, the fee is higher for the transaction that has a negative Net-new-UTXO. After Segregated Witness, the transaction fees align with the incentive to minimize new UTXO creation by not inadvertently penalizing transactions with many inputs.
Segregated Witness therefore has two main effects on the fees paid by bitcoin users. Firstly, segwit reduces the overall cost of transactions by discounting witness data and increasing the capacity of the bitcoin blockchain. Secondly, segwit’s discount on witness data corrects a misalignment of incentives that may have inadvertently created more bloat in the UTXO set.
Appendix E: Bitcore
Bitcore is a suite of tools provided by BitPay. Its goal is to provide easy-to-use tools for Bitcoin developers. Almost all of Bitcore’s code is written in JavaScript. There are some modules written specifically for NodeJS. Finally, the "node" module of Bitcore includes Bitcoin Core’s C++ code. Please see https://bitcore.io for more information.
Bitcore’s Feature List
-
Bitcoin full node (bitcore-node)
-
Block explorer (insight)
-
Block, transaction, and wallet utilities (bitcore-lib)
-
Communicating directly with Bitcoin’s P2P network (bitcore-p2p)
-
Seed entropy mnemonic generation (bitcore-mnemonic)
-
Payment protocol (bitcore-payment-protocol)
-
Message verification and signing (bitcore-message)
-
Elliptic curve Integrated Encryption Scheme (bitcore-ecies)
-
Wallet service (bitcore-wallet-service)
-
Wallet client (bitcore-wallet-client)
-
Playground (bitcore-playground)
-
Integrating services directly with Bitcoin Core (bitcore-node)
Bitcore Library Examples
Prerequisities
-
NodeJS >= 4.x or use our hosted online playground
If using NodeJS and the node REPL:
$ npm install -g bitcore-lib bitcore-p2p $ NODE_PATH=$(npm list -g | head -1)/node_modules node
Wallet Examples using bitcore-lib
Creating a new bitcoin address with associated private key:
> bitcore = require('bitcore-lib')
> privateKey = new bitcore.PrivateKey()
> address = privateKey.toAddress().toString()Creating a hierarchical deterministic private key and address:
> hdPrivateKey = bitcore.HDPrivateKey()
> hdPublicKey = bitcore.HDPublicKey(hdPrivateKey)
> hdAddress = new bitcore.Address(hdPublicKey.publicKey).toString()Creating and signing a transaction from a UTXO:
> utxo = {
txId: transaction id containing an unspent output,
outputIndex: output indexi e.g. 0,
address: addressOfUtxo,
script: bitcore.Script.buildPublicKeyHashOut(addressOfUtxo).toString(),
satoshis: amount sent to the address
}
> fee = 3000 //set appropriately for conditions on the network
> tx = new bitcore.Transaction()
.from(utxo)
.to(address, 35000)
.fee(fee)
.enableRBF()
.sign(privateKeyOfUtxo)Replace the last transaction in the mempool (replace-by-fee):
> rbfTx = new Transaction()
.from(utxo)
.to(address, 35000)
.fee(fee*2)
.enableRBF()
.sign(privateKeyOfUtxo);
> tx.serialize();
> rbfTx.serialize();Broadcasting a transaction to the Bitcoin network (note: broadcast valid transactions only; refer to https://bitnodes.21.co/nodes for peer hosts):
-
Copy the code below into a file called broadcast.js.
-
The
txandrbfTxvariables are the output oftx.serialize()andrbfTx.serialize(), respectively. -
In order to replace-by-fee, the peer must support bitcoind option
mempoolreplaceand have it set to1. -
Run the file node broadcast.js:
var p2p = require('bitcore-p2p');
var bitcore = require('bitcore-lib');
var tx = new bitcore.Transaction('output from serialize function');
var rbfTx = new bitcore.Transaction('output from serialize function');
var host = 'ip address'; //use valid peer listening on tcp 8333
var peer = new p2p.Peer({host: host});
var messages = new p2p.Messages();
peer.on('ready', function() {
var txs = [messages.Transaction(tx), messages.Transaction(rbfTx)];
var index = 0;
var interval = setInterval(function() {
peer.sendMessage(txs[index++]);
console.log('tx: ' + index + ' sent');
if (index === txs.length) {
clearInterval(interval);
console.log('disconnecting from peer: ' + host);
peer.disconnect();
}
}, 2000);
});
peer.connect();Appendix F: pycoin, ku, and tx
The Python library pycoin, originally written and maintained by Richard Kiss, is a Python-based library that supports manipulation of bitcoin keys and transactions, even supporting the scripting language enough to properly deal with nonstandard transactions.
The pycoin library supports both Python 2 (2.7.x) and Python 3 (after 3.3) and comes with some handy command-line utilities, ku and tx.
Key Utility (KU)
The command-line utility ku ("key utility") is a Swiss Army knife for manipulating keys. It supports BIP-32 keys, WIF, and addresses (bitcoin and alt coins). Following are some examples.
Create a BIP-32 key using the default entropy sources of GPG and /dev/random:
$ ku create
input : create
network : Bitcoin
wallet key : xprv9s21ZrQH143K3LU5ctPZTBnb9kTjA5Su9DcWHvXJemiJBsY7VqXUG7hipgdWaU
m2nhnzdvxJf5KJo9vjP2nABX65c5sFsWsV8oXcbpehtJi
public version : xpub661MyMwAqRbcFpYYiuvZpKjKhnJDZYAkWSY76JvvD7FH4fsG3Nqiov2CfxzxY8
DGcpfT56AMFeo8M8KPkFMfLUtvwjwb6WPv8rY65L2q8Hz
tree depth : 0
fingerprint : 9d9c6092
parent f'print : 00000000
child index : 0
chain code : 80574fb260edaa4905bc86c9a47d30c697c50047ed466c0d4a5167f6821e8f3c
private key : yes
secret exponent : 112471538590155650688604752840386134637231974546906847202389294096567806844862
hex : f8a8a28b28a916e1043cc0aca52033a18a13cab1638d544006469bc171fddfbe
wif : L5Z54xi6qJusQT42JHA44mfPVZGjyb4XBRWfxAzUWwRiGx1kV4sP
uncompressed : 5KhoEavGNNH4GHKoy2Ptu4KfdNp4r56L5B5un8FP6RZnbsz5Nmb
public pair x : 76460638240546478364843397478278468101877117767873462127021560368290114016034
public pair y : 59807879657469774102040120298272207730921291736633247737077406753676825777701
x as hex : a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
y as hex : 843a0f6ed9c0eb1962c74533795406914fe3f1957c5238951f4fe245a4fcd625
y parity : odd
key pair as sec : 03a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
uncompressed : 04a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
843a0f6ed9c0eb1962c74533795406914fe3f1957c5238951f4fe245a4fcd625
hash160 : 9d9c609247174ae323acfc96c852753fe3c8819d
uncompressed : 8870d869800c9b91ce1eb460f4c60540f87c15d7
Bitcoin address : 1FNNRQ5fSv1wBi5gyfVBs2rkNheMGt86sp
uncompressed : 1DSS5isnH4FsVaLVjeVXewVSpfqktdiQAMCreate a BIP-32 key from a passphrase:
|
Warning
|
The passphrase in this example is way too easy to guess. |
$ ku P:foo
input : P:foo
network : Bitcoin
wallet key : xprv9s21ZrQH143K31AgNK5pyVvW23gHnkBq2wh5aEk6g1s496M8ZMjxncCKZKgb5j
ZoY5eSJMJ2Vbyvi2hbmQnCuHBujZ2WXGTux1X2k9Krdtq
public version : xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWoQayvtS
VYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zy
tree depth : 0
fingerprint : 5d353a2e
parent f'print : 00000000
child index : 0
chain code : 5eeb1023fd6dd1ae52a005ce0e73420821e1d90e08be980a85e9111fd7646bbc
private key : yes
secret exponent : 65825730547097305716057160437970790220123864299761908948746835886007793998275
hex : 91880b0e3017ba586b735fe7d04f1790f3c46b818a2151fb2def5f14dd2fd9c3
wif : L26c3H6jEPVSqAr1usXUp9qtQJw6NHgApq6Ls4ncyqtsvcq2MwKH
uncompressed : 5JvNzA5vXDoKYJdw8SwwLHxUxaWvn9mDea6k1vRPCX7KLUVWa7W
public pair x : 81821982719381104061777349269130419024493616650993589394553404347774393168191
public pair y : 58994218069605424278320703250689780154785099509277691723126325051200459038290
x as hex : b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
y as hex : 826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52
y parity : even
key pair as sec : 02b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
uncompressed : 04b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52
hash160 : 5d353a2ecdb262477172852d57a3f11de0c19286
uncompressed : e5bd3a7e6cb62b4c820e51200fb1c148d79e67da
Bitcoin address : 19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAii
uncompressed : 1MwkRkogzBRMehBntgcq2aJhXCXStJTXHTGet info as JSON:
$ ku P:foo -P -j{ "y_parity": "even", "public_pair_y_hex": "826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52", "private_key": "no", "parent_fingerprint": "00000000", "tree_depth": "0", "network": "Bitcoin", "btc_address_uncompressed": "1MwkRkogzBRMehBntgcq2aJhXCXStJTXHT", "key_pair_as_sec_uncompressed": "04b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52", "public_pair_x_hex": "b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f", "wallet_key": "xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWoQayvtSVYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zy", "chain_code": "5eeb1023fd6dd1ae52a005ce0e73420821e1d90e08be980a85e9111fd7646bbc", "child_index": "0", "hash160_uncompressed": "e5bd3a7e6cb62b4c820e51200fb1c148d79e67da", "btc_address": "19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAii", "fingerprint": "5d353a2e", "hash160": "5d353a2ecdb262477172852d57a3f11de0c19286", "input": "P:foo", "public_pair_x": "81821982719381104061777349269130419024493616650993589394553404347774393168191", "public_pair_y": "58994218069605424278320703250689780154785099509277691723126325051200459038290", "key_pair_as_sec": "02b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f" }
Public BIP32 key:
$ ku -w -P P:foo
xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWoQayvtSVYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zyGenerate a subkey:
$ ku -w -s3/2 P:foo
xprv9wTErTSkjVyJa1v4cUTFMFkWMe5eu8ErbQcs9xajnsUzCBT7ykHAwdrxvG3g3f6BFk7ms5hHBvmbdutNmyg6iogWKxx6mefEw4M8EroLgKjHardened subkey:
$ ku -w -s3/2H P:foo
xprv9wTErTSu5AWGkDeUPmqBcbZWX1xq85ZNX9iQRQW9DXwygFp7iRGJo79dsVctcsCHsnZ3XU3DhsuaGZbDh8iDkBN45k67UKsJUXM1JfRCdn1WIF:
$ ku -W P:foo
L26c3H6jEPVSqAr1usXUp9qtQJw6NHgApq6Ls4ncyqtsvcq2MwKHAddress:
$ ku -a P:foo
19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAiiGenerate a bunch of subkeys:
$ ku P:foo -s 0/0-5 -w
xprv9xWkBDfyBXmZjBG9EiXBpy67KK72fphUp9utJokEBFtjsjiuKUUDF5V3TU8U8cDzytqYnSekc8bYuJS8G3bhXxKWB89Ggn2dzLcoJsuEdRK
xprv9xWkBDfyBXmZnzKf3bAGifK593gT7WJZPnYAmvc77gUQVej5QHckc5Adtwxa28ACmANi9XhCrRvtFqQcUxt8rUgFz3souMiDdWxJDZnQxzx
xprv9xWkBDfyBXmZqdXA8y4SWqfBdy71gSW9sjx9JpCiJEiBwSMQyRxan6srXUPBtj3PTxQFkZJAiwoUpmvtrxKZu4zfsnr3pqyy2vthpkwuoVq
xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuqxYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
xprv9xWkBDfyBXmZv2q3N66hhZ8DAcEnQDnXML1J62krJAcf7Xb1HJwuW2VMJQrCofY2jtFXdiEY8UsRNJfqK6DAdyZXoMvtaLHyWQx3FS4A9zw
xprv9xWkBDfyBXmZw4jEYXUHYc9fT25k9irP87n2RqfJ5bqbjKdT84Mm7Wtc2xmzFuKg7iYf7XFHKkSsaYKWKJbR54bnyAD9GzjUYbAYTtN4ruoGenerate the corresponding addresses:
$ ku P:foo -s 0/0-5 -a
1MrjE78H1R1rqdFrmkjdHnPUdLCJALbv3x
1AnYyVEcuqeoVzH96zj1eYKwoWfwte2pxu
1GXr1kZfxE1FcK6ZRD5sqqqs5YfvuzA1Lb
116AXZc4bDVQrqmcinzu4aaPdrYqvuiBEK
1Cz2rTLjRM6pMnxPNrRKp9ZSvRtj5dDUML
1WstdwPnU6HEUPme1DQayN9nm6j7nDVEMGenerate the corresponding WIFs:
$ ku P:foo -s 0/0-5 -W
L5a4iE5k9gcJKGqX3FWmxzBYQc29PvZ6pgBaePLVqT5YByEnBomx
Kyjgne6GZwPGB6G6kJEhoPbmyjMP7D5d3zRbHVjwcq4iQXD9QqKQ
L4B3ygQxK6zH2NQGxLDee2H9v4Lvwg14cLJW7QwWPzCtKHdWMaQz
L2L2PZdorybUqkPjrmhem4Ax5EJvP7ijmxbNoQKnmTDMrqemY8UF
L2oD6vA4TUyqPF8QG4vhUFSgwCyuuvFZ3v8SKHYFDwkbM765Nrfd
KzChTbc3kZFxUSJ3Kt54cxsogeFAD9CCM4zGB22si8nfKcThQn8CCheck that it works by choosing a BIP32 string (the one corresponding to subkey 0/3):
$ ku -W xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuqxYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
L2L2PZdorybUqkPjrmhem4Ax5EJvP7ijmxbNoQKnmTDMrqemY8UF
$ ku -a xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuqxYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
116AXZc4bDVQrqmcinzu4aaPdrYqvuiBEKYep, looks familiar.
From secret exponent:
$ ku 1
input : 1
network : Bitcoin
secret exponent : 1
hex : 1
wif : KwDiBf89QgGbjEhKnhXJuH7LrciVrZi3qYjgd9M7rFU73sVHnoWn
uncompressed : 5HpHagT65TZzG1PH3CSu63k8DbpvD8s5ip4nEB3kEsreAnchuDf
public pair x : 55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y : 32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex : 79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex : 483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity : even
key pair as sec : 0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed : 0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160 : 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed : 91b24bf9f5288532960ac687abb035127b1d28a5
Bitcoin address : 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH
uncompressed : 1EHNa6Q4Jz2uvNExL497mE43ikXhwF6kZmLitecoin version:
$ ku -nL 1
input : 1
network : Litecoin
secret exponent : 1
hex : 1
wif : T33ydQRKp4FCW5LCLLUB7deioUMoveiwekdwUwyfRDeGZm76aUjV
uncompressed : 6u823ozcyt2rjPH8Z2ErsSXJB5PPQwK7VVTwwN4mxLBFrao69XQ
public pair x : 55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y : 32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex : 79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex : 483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity : even
key pair as sec : 0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed : 0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160 : 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed : 91b24bf9f5288532960ac687abb035127b1d28a5
Litecoin address : LVuDpNCSSj6pQ7t9Pv6d6sUkLKoqDEVUnJ
uncompressed : LYWKqJhtPeGyBAw7WC8R3F7ovxtzAiubdMDogecoin WIF:
$ ku -nD -W 1
QNcdLVw8fHkixm6NNyN6nVwxKek4u7qrioRbQmjxac5TVoTtZuotFrom public pair (on Testnet):
$ ku -nT 55066263022277343669578718895168534326250603453777594175500187360389116729240,even
input : 550662630222773436695787188951685343262506034537775941755001873603
89116729240,even
network : Bitcoin testnet
public pair x : 55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y : 32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex : 79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex : 483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity : even
key pair as sec : 0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed : 0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160 : 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed : 91b24bf9f5288532960ac687abb035127b1d28a5
Bitcoin testnet address : mrCDrCybB6J1vRfbwM5hemdJz73FwDBC8r
uncompressed : mtoKs9V381UAhUia3d7Vb9GNak8QvmcsmeFrom hash160:
$ ku 751e76e8199196d454941c45d1b3a323f1433bd6
input : 751e76e8199196d454941c45d1b3a323f1433bd6
network : Bitcoin
hash160 : 751e76e8199196d454941c45d1b3a323f1433bd6
Bitcoin address : 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMHAs a Dogecoin address:
$ ku -nD 751e76e8199196d454941c45d1b3a323f1433bd6
input : 751e76e8199196d454941c45d1b3a323f1433bd6
network : Dogecoin
hash160 : 751e76e8199196d454941c45d1b3a323f1433bd6
Dogecoin address : DFpN6QqFfUm3gKNaxN6tNcab1FArL9cZLETransaction Utility (TX)
The command-line utility tx will display transactions in human-readable form, fetch base transactions from pycoin’s transaction cache or from web services (blockchain.info and biteasy.com are currently supported), merge transactions, add or delete inputs or outputs, and sign transactions.
Following are some examples.
View the famous "pizza" transaction:
$ tx 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
warning: consider setting environment variable PYCOIN_CACHE_DIR=~/.pycoin_cache to cache transactions fetched via web services
warning: no service providers found for get_tx; consider setting environment variable PYCOIN_SERVICE_PROVIDERS=BLOCKR_IO:BLOCKCHAIN_INFO:BITEASY:BLOCKEXPLORER
usage: tx [-h] [-t TRANSACTION_VERSION] [-l LOCK_TIME] [-n NETWORK] [-a]
[-i address] [-f path-to-private-keys] [-g GPG_ARGUMENT]
[--remove-tx-in tx_in_index_to_delete]
[--remove-tx-out tx_out_index_to_delete] [-F transaction-fee] [-u]
[-b BITCOIND_URL] [-o path-to-output-file]
argument [argument ...]
tx: error: can't find Tx with id 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2aOops! We don’t have web services set up. Let’s do that now:
$ PYCOIN_CACHE_DIR=~/.pycoin_cache $ PYCOIN_SERVICE_PROVIDERS=BLOCKR_IO:BLOCKCHAIN_INFO:BITEASY:BLOCKEXPLORER $ export PYCOIN_CACHE_DIR PYCOIN_SERVICE_PROVIDERS
It’s not done automatically so a command-line tool won’t leak potentially private information about what transactions you’re interested in to a third-party website. If you don’t care, you could put these lines into your .profile.
Let’s try again:
$ tx 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
Version: 1 tx hash 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a 159 bytes
TxIn count: 1; TxOut count: 1
Lock time: 0 (valid anytime)
Input:
0: (unknown) from 1e133f7de73ac7d074e2746a3d6717dfc99ecaa8e9f9fade2cb8b0b20a5e0441:0
Output:
0: 1CZDM6oTttND6WPdt3D6bydo7DYKzd9Qik receives 10000000.00000 mBTC
Total output 10000000.00000 mBTC
including unspents in hex dump since transaction not fully signed
010000000141045e0ab2b0b82cdefaf9e9a8ca9ec9df17673d6a74e274d0c73ae77d3f131e000000004a493046022100a7f26eda874931999c90f87f01ff1ffc76bcd058fe16137e0e63fdb6a35c2d78022100a61e9199238eb73f07c8f209504c84b80f03e30ed8169edd44f80ed17ddf451901ffffffff010010a5d4e80000001976a9147ec1003336542cae8bded8909cdd6b5e48ba0ab688ac00000000
** can't validate transaction as source transactions missingThe final line appears because to validate the transactions' signatures, you technically need the source transactions. So let’s add -a to augment the transactions with source information:
$ tx -a 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
warning: transaction fees recommendations casually calculated and estimates may be incorrect
warning: transaction fee lower than (casually calculated) expected value of 0.1 mBTC, transaction might not propogate
Version: 1 tx hash 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a 159 bytes
TxIn count: 1; TxOut count: 1
Lock time: 0 (valid anytime)
Input:
0: 17WFx2GQZUmh6Up2NDNCEDk3deYomdNCfk from 1e133f7de73ac7d074e2746a3d6717dfc99ecaa8e9f9fade2cb8b0b20a5e0441:0 10000000.00000 mBTC sig ok
Output:
0: 1CZDM6oTttND6WPdt3D6bydo7DYKzd9Qik receives 10000000.00000 mBTC
Total input 10000000.00000 mBTC
Total output 10000000.00000 mBTC
Total fees 0.00000 mBTC
010000000141045e0ab2b0b82cdefaf9e9a8ca9ec9df17673d6a74e274d0c73ae77d3f131e000000004a493046022100a7f26eda874931999c90f87f01ff1ffc76bcd058fe16137e0e63fdb6a35c2d78022100a61e9199238eb73f07c8f209504c84b80f03e30ed8169edd44f80ed17ddf451901ffffffff010010a5d4e80000001976a9147ec1003336542cae8bded8909cdd6b5e48ba0ab688ac00000000
all incoming transaction values validatedNow, let’s look at unspent outputs for a specific address (UTXO). In block #1, we see a coinbase transaction to 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX. Let’s use fetch_unspent to find all coins in this address:
$ fetch_unspent 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX
a3a6f902a51a2cbebede144e48a88c05e608c2cce28024041a5b9874013a1e2a/0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/333000
cea36d008badf5c7866894b191d3239de9582d89b6b452b596f1f1b76347f8cb/31/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/10000
065ef6b1463f552f675622a5d1fd2c08d6324b4402049f68e767a719e2049e8d/86/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/10000
a66dddd42f9f2491d3c336ce5527d45cc5c2163aaed3158f81dc054447f447a2/0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/10000
ffd901679de65d4398de90cefe68d2c3ef073c41f7e8dbec2fb5cd75fe71dfe7/0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/100
d658ab87cc053b8dbcfd4aa2717fd23cc3edfe90ec75351fadd6a0f7993b461d/5/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/911
36ebe0ca3237002acb12e1474a3859bde0ac84b419ec4ae373e63363ebef731c/1/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/100000
fd87f9adebb17f4ebb1673da76ff48ad29e64b7afa02fda0f2c14e43d220fe24/0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/1
dfdf0b375a987f17056e5e919ee6eadd87dad36c09c4016d4a03cea15e5c05e3/1/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/1337
cb2679bfd0a557b2dc0d8a6116822f3fcbe281ca3f3e18d3855aa7ea378fa373/0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/1337
d6be34ccf6edddc3cf69842dce99fe503bf632ba2c2adb0f95c63f6706ae0c52/1/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/2000000
0e3e2357e806b6cdb1f70b54c3a3a17b6714ee1f0e68bebb44a74b1efd512098/0/410496b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52da7589379515d4e0a604f8141781e62294721166bf621e73a82cbf2342c858eeac/5000000000Appendix G: Bitcoin Explorer (bx) Commands
Bitcoin Explorer (bx) is a command-line tool that offers a variety of commands for key management and transaction construction. It is part of the libbitcoin bitcoin library.
Usage: bx COMMAND [--help]
Info: The bx commands are:
address-decode
address-embed
address-encode
address-validate
base16-decode
base16-encode
base58-decode
base58-encode
base58check-decode
base58check-encode
base64-decode
base64-encode
bitcoin160
bitcoin256
btc-to-satoshi
ec-add
ec-add-secrets
ec-multiply
ec-multiply-secrets
ec-new
ec-to-address
ec-to-public
ec-to-wif
fetch-balance
fetch-header
fetch-height
fetch-history
fetch-stealth
fetch-tx
fetch-tx-index
hd-new
hd-private
hd-public
hd-to-address
hd-to-ec
hd-to-public
hd-to-wif
help
input-set
input-sign
input-validate
message-sign
message-validate
mnemonic-decode
mnemonic-encode
ripemd160
satoshi-to-btc
script-decode
script-encode
script-to-address
seed
send-tx
send-tx-node
send-tx-p2p
settings
sha160
sha256
sha512
stealth-decode
stealth-encode
stealth-public
stealth-secret
stealth-shared
tx-decode
tx-encode
uri-decode
uri-encode
validate-tx
watch-address
wif-to-ec
wif-to-public
wrap-decode
wrap-encodeFor more information, see the Bitcoin Explorer homepage and Bitcoin Explorer user documentation.
Examples of bx Command Use
Let’s look at some examples of using Bitcoin Explorer commands to experiment with keys and addresses.
Generate a random "seed" value using the seed command, which uses the operating system’s random number generator. Pass the seed to the ec-new command to generate a new private key. We save the standard output into the file private_key:
$ bx seed | bx ec-new > private_key
$ cat private_key
73096ed11ab9f1db6135857958ece7d73ea7c30862145bcc4bbc7649075de474Now, generate the public key from that private key using the ec-to-public command. We pass the private_key file into the standard input and save the standard output of the command into a new file public_key:
$ bx ec-to-public < private_key > public_key
$ cat public_key
02fca46a6006a62dfdd2dbb2149359d0d97a04f430f12a7626dd409256c12be500We can reformat the public_key as an address using the ec-to-address command. We pass the public_key into standard input:
$ bx ec-to-address < public_key
17re1S4Q8ZHyCP8Kw7xQad1Lr6XUzWUnkGKeys generated in this manner produce a type-0 nondeterministic wallet. That means that each key is generated from an independent seed. Bitcoin Explorer commands can also generate keys deterministically, in accordance with BIP-32. In this case, a "master" key is created from a seed and then extended deterministically to produce a tree of subkeys, resulting in a type-2 deterministic wallet.
First, we use the seed and hd-new commands to generate a master key that will be used as the basis to derive a hierarchy of keys:
$ bx seed > seed
$ cat seed
eb68ee9f3df6bd4441a9feadec179ff1
$ bx hd-new < seed > master
$ cat master
xprv9s21ZrQH143K2BEhMYpNQoUvAgiEjArAVaZaCTgsaGe6LsAnwubeiTcDzd23mAoyizm9cApe51gNfLMkBqkYoWWMCRwzfuJk8RwF1SVEpAQWe now use the hd-private command to generate a hardened "account" key and a sequence of two private keys within the account:
$ bx hd-private --hard < master > account
$ cat account
xprv9vkDLt81dTKjwHB8fsVB5QK8cGnzveChzSrtCfvu3aMWvQaThp59ueufuyQ8Qi3qpjk4aKsbmbfxwcgS8PYbgoR2NWHeLyvg4DhoEE68A1n
$ bx hd-private --index 0 < account
xprv9xHfb6w1vX9xgZyPNXVgAhPxSsEkeRcPHEUV5iJcVEsuUEACvR3NRY3fpGhcnBiDbvG4LgndirDsia1e9F3DWPkX7Tp1V1u97HKG1FJwUpU
$ bx hd-private --index 1 < account
xprv9xHfb6w1vX9xjc8XbN4GN86jzNAZ6xHEqYxzbLB4fzHFd6VqCLPGRZFsdjsuMVERadbgDbziCRJru9n6tzEWrASVpEdrZrFidt1RDfn4yA3Next, we use the hd-public command to generate the corresponding sequence of two public keys:
$ bx hd-public --index 0 < account
xpub6BH1zcTuktiFu43rUZ2gXqLgzu5F3tLEeTQ5t6iE3aQtM2VMTxMcyLN9fYHiGhGpQe9QQYmqL2eYPFJ3vezHz5wzaSW4FiGrseNDR4LKqTy
$ bx hd-public --index 1 < account
xpub6BH1zcTuktiFx6CzhPbGjG3UYQ13WR16CmtbPiagEKpEVtpyjshWyMaMV1cn7nUPUkgQHPVXJVqsrA8xWbGQDhohEcDFTEYMvYzwRD7Juf8The public keys can also be derived from their corresponding private keys using the hd-to-public command:
$ bx hd-private --index 0 < account | bx hd-to-public
xpub6BH1zcTuktiFu43rUZ2gXqLgzu5F3tLEeTQ5t6iE3aQtM2VMTxMcyLN9fYHiGhGpQe9QQYmqL2eYPFJ3vezHz5wzaSW4FiGrseNDR4LKqTy
$ bx hd-private --index 1 < account | bx hd-to-public
xpub6BH1zcTuktiFx6CzhPbGjG3UYQ13WR16CmtbPiagEKpEVtpyjshWyMaMV1cn7nUPUkgQHPVXJVqsrA8xWbGQDhohEcDFTEYMvYzwRD7Juf8We can generate a practically limitless number of keys in a deterministic chain, all derived from a single seed. This technique is used in many wallet applications to generate keys that can be backed up and restored with a single seed value. This is easier than having to back up the wallet with all its randomly generated keys every time a new key is created.
The seed can be encoded using the mnemonic-encode command:
$ bx hd-mnemonic < seed > words
adore repeat vision worst especially veil inch woman cast recall dwell appreciateThe seed can then be decoded using the mnemonic-decode command:
$ bx mnemonic-decode < words
eb68ee9f3df6bd4441a9feadec179ff1Mnemonic encoding can make the seed easier to record and even remember.